



生物多样性 ›› 2009, Vol. 17 ›› Issue (1): 43-50. DOI: 10.3724/SP.J.1003.2009.08148 cstr: 32101.14.SP.J.1003.2009.08148
收稿日期:2008-06-20
接受日期:2008-12-29
出版日期:2009-01-20
发布日期:2009-01-20
通讯作者:
胡庭兴
作者简介:* E-mail: hutx001@yahoo.com.cn基金资助:
Anjiu Zhao, Tingxing Hu*( ), Xiaohong Chen
), Xiaohong Chen
Received:2008-06-20
Accepted:2008-12-29
Online:2009-01-20
Published:2009-01-20
Contact:
Tingxing Hu
摘要:
为了解植物群落在多尺度下的空间变异规律及其对空间尺度的依赖, 以川西南山地阔叶混交林为对象, 在有代表性的地段设立100 m×100 m样地, 采用传统的罗盘仪对树体的相对空间位置进行定位, 运用主轴邻距法(principal coordinates of neighbor matrices, PCNM)对群落空间结构的多尺度(100 m内)特征进行了研究。结果表明,群落均匀度指数、空隙度和开度、林分胸高断面积和林分密度在大尺度上表现出显著的空间结构。在不同的尺度下, 林分密度、叶面积指数和林下地表直接辐射都对均匀度指数有影响, 林分密度、林下地表直接辐射、生物量和空隙度都对土壤有机质含量有显著影响, 群落结构与环境因子都表现出明显的空间结构。PCNM分析可获取样本间空间关系在不同尺度上的分解向量, 与群落结构显著相关的PCNM因子即是群落或生境在该尺度上所表现出的显著的空间结构。典型相关分析结果表明群落结构因子和光因子相关性显著, 两者都与PCNM变量极显著相关且相互影响,表明群落结构和光因子都表现出显著的空间结构。因此, 利用PCNM对群落结构进行空间分析有助于理解群落空间异质性对尺度的依赖。
赵安玖, 胡庭兴, 陈小红 (2009) 西南山地阔叶混交林群落空间结构的多尺度特征. 生物多样性, 17, 43-50. DOI: 10.3724/SP.J.1003.2009.08148.
Anjiu Zhao, Tingxing Hu, Xiaohong Chen (2009) Multiple-scale spatial analysis of community structure in a mountainous mixed evergreen-deciduous broad-leaved forest, southwest China. Biodiversity Science, 17, 43-50. DOI: 10.3724/SP.J.1003.2009.08148.
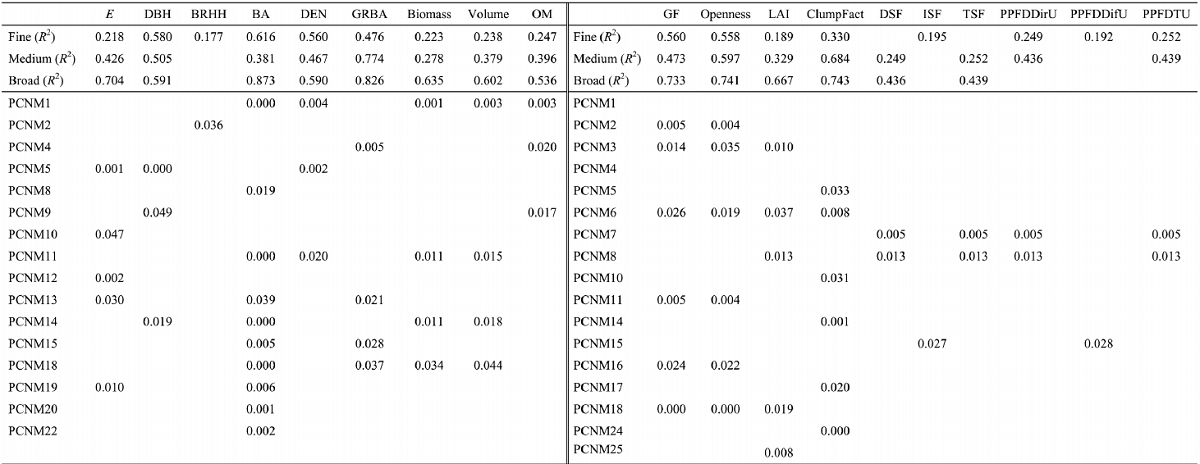 |
表1 各変量在不同尺度下的PCNM解释(表中数据为不同尺度的R2值和各参数的t-检验的P值
Table 1 Interpretation variance of the PCNM variables at fine, medium, and broad scales. Data in the table showed R2 of each spatial submodel and P-values of regression coefficients of the environmental variables in the model considered.
 |
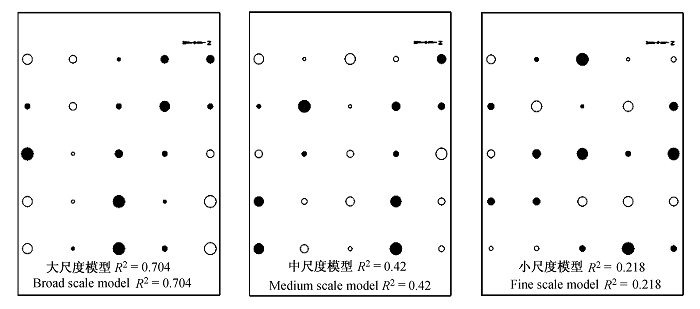
图1 均匀度指数(E)的PCNM空间模型及子模型
Fig. 1 PCNM spatial model and sub-model of the evenness index (E). PCNM analysis of sampling sites which represents broad-scale, medium-scale, and fine-scale model of species diversity. Filled and empty bubbles represented positive and negative values, respectively.
| 均匀度指数 Pielou evenness index | 大尺度 Broad scale | 中尺度Medium scale | 小尺度 Fine scale | |
|---|---|---|---|---|
| R2 of environments | 0.674 | 0.964 | 0.575 | 0.757 |
| 胸径 Diameter at breast height | 0.018 | 0.023 | 0.017 | |
| 树高 Height | 0.038 | 0.042 | ||
| 冠层高 Canopy height | 0.021 | 0.007 | 0.070 | |
| 林分密度 Stand density | 0.011 | 0.010 | 0.0001 | 0.012 |
| 空隙度 GapFraction | 0.075 | 0.077 | ||
| 叶面积指数 Leaf area index | 0.066 | 0.098 | 0.001 | |
| 聚集指数 Index of clumping leaves | 0.036 | 0.100 | 0.031 | |
| 林下地表直接辐射 Direct radiation | 0.032 | 0.012 | 0.033 | |
| 有机质 Organic matters contents | 0.045 | 0.041 | 0.052 | |
| 开度 Openness | 0.039 | |||
| 冠层下散射的光通量密度 Diffuse photosynthetic photon flux density under canopy | 0.086 |
表2 均匀度指数(E)与空间和环境变量模型(表中数据为环境变量的R2值和各参数的t-检验显著的P值)
Table 2 R2 and probabilities related to the spatial analysis of environmental variables. Data in the table showed R2 of the regression of the submodel (fitted values) on a subset of forward-selected environmental variables and P-values of the regression coefficients of the environmental variables.
| 均匀度指数 Pielou evenness index | 大尺度 Broad scale | 中尺度Medium scale | 小尺度 Fine scale | |
|---|---|---|---|---|
| R2 of environments | 0.674 | 0.964 | 0.575 | 0.757 |
| 胸径 Diameter at breast height | 0.018 | 0.023 | 0.017 | |
| 树高 Height | 0.038 | 0.042 | ||
| 冠层高 Canopy height | 0.021 | 0.007 | 0.070 | |
| 林分密度 Stand density | 0.011 | 0.010 | 0.0001 | 0.012 |
| 空隙度 GapFraction | 0.075 | 0.077 | ||
| 叶面积指数 Leaf area index | 0.066 | 0.098 | 0.001 | |
| 聚集指数 Index of clumping leaves | 0.036 | 0.100 | 0.031 | |
| 林下地表直接辐射 Direct radiation | 0.032 | 0.012 | 0.033 | |
| 有机质 Organic matters contents | 0.045 | 0.041 | 0.052 | |
| 开度 Openness | 0.039 | |||
| 冠层下散射的光通量密度 Diffuse photosynthetic photon flux density under canopy | 0.086 |
| 有机质 Organic matter content | 大尺度 Broad scale | 中尺度Medium scale | 小尺度 Fine scale | |
|---|---|---|---|---|
| R2 of environment | 0.701 | 0.967 | 0.856 | 0.944 |
| 胸径 Diameter at breast height | 0.002 | 0.015 | 0.004 | 0.008 |
| 冠层高 Canopy height | 0.033 | 0.005 | 0.001 | 0.091 |
| 林分密度 Stand density | 0.003 | 0.008 | ||
| 生长速率 Growth ratio of BA | 0.005 | 0.017 | 0.002 | |
| 生物量 Biomass | 0.0001 | 0.055 | 0.006 | 0.068 |
| 空隙度 GapFraction | 0.010 | 0.002 | 0.018 | 0.071 |
| 叶面积指数 Leaf area index | 0.042 | 0.029 | 0.040 | |
| 聚集指数 Index of clumping leaves | 0.007 | 0.008 | 0.033 | |
| 林下地表直接辐射 Direct radiation | 0.001 | 0.030 | 0.004 | 0.085 |
| 林下地表散射 Diffuse radiation | 0.015 | 0.012 | 0.003 | |
| 冠层下散射的光通量密度 Diffuse photosynthetic photon flux density under canopy | 0.022 | 0.043 | ||
| 开度 Openness | 0.011 |
表3 土壤有机质与空间和环境变量模型(表中数据为环境变量的R2值和各参数的t-检验显著的P值)
Table 3 R2 and probabilities related to the spatial analysis of environmental variables. Data in the table showed R2 of the regression of the submodel (fitted values) on a subset of forward-selected environmental variables and P-values of the regression coefficients of the environmental variables.
| 有机质 Organic matter content | 大尺度 Broad scale | 中尺度Medium scale | 小尺度 Fine scale | |
|---|---|---|---|---|
| R2 of environment | 0.701 | 0.967 | 0.856 | 0.944 |
| 胸径 Diameter at breast height | 0.002 | 0.015 | 0.004 | 0.008 |
| 冠层高 Canopy height | 0.033 | 0.005 | 0.001 | 0.091 |
| 林分密度 Stand density | 0.003 | 0.008 | ||
| 生长速率 Growth ratio of BA | 0.005 | 0.017 | 0.002 | |
| 生物量 Biomass | 0.0001 | 0.055 | 0.006 | 0.068 |
| 空隙度 GapFraction | 0.010 | 0.002 | 0.018 | 0.071 |
| 叶面积指数 Leaf area index | 0.042 | 0.029 | 0.040 | |
| 聚集指数 Index of clumping leaves | 0.007 | 0.008 | 0.033 | |
| 林下地表直接辐射 Direct radiation | 0.001 | 0.030 | 0.004 | 0.085 |
| 林下地表散射 Diffuse radiation | 0.015 | 0.012 | 0.003 | |
| 冠层下散射的光通量密度 Diffuse photosynthetic photon flux density under canopy | 0.022 | 0.043 | ||
| 开度 Openness | 0.011 |
| 第一组变量 First group variables | 第二组变量 Second group variables | 典型相关系数 Canonical correlation coefficients | 典型变量 Canonical variables |
|---|---|---|---|
| 结构因子 Structure variables | 光因子 Light variables | λ1 = 0.940634 | V1 = -2.8062DBH+1.1367Height+0.5801BRHH+2.7372BA-2.3781DEN -0.1896GRBA+0.179biomass-1.6385 volume W1 = -21.68 GF+22.62Openness-0.47LAI-0.81 ClumpFact-798.89DSF-48.90ISF+ 826.07TSF-218.08PPFDDirU+19.22PPFDDifU+201.94 PPFDTU |
| λ2 = 0.64406 | |||
| λ3 = 0.493505 | |||
| λ4 = 0.432535 | |||
| 结构因子 Structure variables | 空间因子(PCNM) | λ1 = 0.9998 | V1 = 2.1582 DBH+0.5098 Height-1.4834 BRHH-0.2816 BA+1.585 DEN+0.0917 biomass+0.1322 volume W1 = 0.449 PCNM1+1.525 PCNM3 +0.627 PCNM4+2.632 PCNM5-1.531 PCNM7+0.093 PCNM8+1.344 PCNM9+1.497 PCNM10+0.152 PCNM11 +0.345 PCNM12-0.121 PCNM13-1.254 PCNM14+0.988 PCNM15-1.764 PCNM18+2.150 PCNM19+0.318 PCNM21-0.253 PCNM22 +1.199 PCNM24+3.262 PCNM25 |
| λ2 = 0.992 | |||
| λ3 = 0.954633 | |||
| λ4 = 0.940490 | |||
| 光因子 Light variables | 空间因子(PCNM) | λ1 = 0.999 | V1 = 25.551GF-27.189Openness-0.591LAI-0.222ClumpFac+1213.001DSF+34.911ISF -698.782TSF-756.670PPFDDirU-19.734 PPFDDifU+238.120 PPFDTU W1 = 0.1105 PCNM2+0.1245 PCNM3+0.3092 PCNM5+0.3640 PCNM6+0.2677 PCNM7+0.2772 PCNM8+0.2036 PCNM9+0.3604 PCNM10+0.2052 PCNM13-0.0062 PCNM14+0.0635 PCNM17+0.2569 PCNM19+0.1649 PCNM21+0.6269 PCNM23+0.1094 PCNM25 |
| λ2 = 0.998333 | |||
| λ3 = 0.968076 | |||
| λ4 = 0.897069 |
表4 群落结构因子和冠层光因子及PCNM组间的典型分析
Table 4 Canonical correlation analysis on community structures and canopy structures as well as relations with PCNM
| 第一组变量 First group variables | 第二组变量 Second group variables | 典型相关系数 Canonical correlation coefficients | 典型变量 Canonical variables |
|---|---|---|---|
| 结构因子 Structure variables | 光因子 Light variables | λ1 = 0.940634 | V1 = -2.8062DBH+1.1367Height+0.5801BRHH+2.7372BA-2.3781DEN -0.1896GRBA+0.179biomass-1.6385 volume W1 = -21.68 GF+22.62Openness-0.47LAI-0.81 ClumpFact-798.89DSF-48.90ISF+ 826.07TSF-218.08PPFDDirU+19.22PPFDDifU+201.94 PPFDTU |
| λ2 = 0.64406 | |||
| λ3 = 0.493505 | |||
| λ4 = 0.432535 | |||
| 结构因子 Structure variables | 空间因子(PCNM) | λ1 = 0.9998 | V1 = 2.1582 DBH+0.5098 Height-1.4834 BRHH-0.2816 BA+1.585 DEN+0.0917 biomass+0.1322 volume W1 = 0.449 PCNM1+1.525 PCNM3 +0.627 PCNM4+2.632 PCNM5-1.531 PCNM7+0.093 PCNM8+1.344 PCNM9+1.497 PCNM10+0.152 PCNM11 +0.345 PCNM12-0.121 PCNM13-1.254 PCNM14+0.988 PCNM15-1.764 PCNM18+2.150 PCNM19+0.318 PCNM21-0.253 PCNM22 +1.199 PCNM24+3.262 PCNM25 |
| λ2 = 0.992 | |||
| λ3 = 0.954633 | |||
| λ4 = 0.940490 | |||
| 光因子 Light variables | 空间因子(PCNM) | λ1 = 0.999 | V1 = 25.551GF-27.189Openness-0.591LAI-0.222ClumpFac+1213.001DSF+34.911ISF -698.782TSF-756.670PPFDDirU-19.734 PPFDDifU+238.120 PPFDTU W1 = 0.1105 PCNM2+0.1245 PCNM3+0.3092 PCNM5+0.3640 PCNM6+0.2677 PCNM7+0.2772 PCNM8+0.2036 PCNM9+0.3604 PCNM10+0.2052 PCNM13-0.0062 PCNM14+0.0635 PCNM17+0.2569 PCNM19+0.1649 PCNM21+0.6269 PCNM23+0.1094 PCNM25 |
| λ2 = 0.998333 | |||
| λ3 = 0.968076 | |||
| λ4 = 0.897069 |
| [1] | Blackburn TM, Gaston KJ (1996) Spatial patterns in the geographic range sizes of bird species in the New World. Philosophical Transactions of the Royal Society of London B, 351, 897-912. |
| [2] | Blackburn TM, Gaston KJ (1996) Spatial patterns in the species richness of birds in the New World. Ecography, 19, 369-376. |
| [3] | Borcard D, Legendre P (1994) Environmental control and spatial structure in ecological communities: an example using oribatid mites (Acari, Oribatei). Environmental and Ecological Statistics, 1, 37-61. |
| [4] | Borcard D, Legendre P (2002) All-scale spatial analysis of ecological data by means of principal coordinates of neighbour matrices. Ecological Modelling, 153, 51-68. |
| [5] | Borcard D, Legendre P, Avois-Jacquet C, Tuomisto H (2004) Dissecting the spatial structure of ecological data at multiple scales. Ecology, 85, 1826-1832. |
| [6] | Borcard D, Legendre P, Drapeau P (1992) Partialling out the spatial component of ecological variation. Ecology, 73, 1045-1055. |
| [7] | Brown MJ, Parker GC (1994) Canopy light transmittance in a chronosequence of mixed-species deciduous forests. Canadian Journal of Forest Research, 24, 1694-1703. |
| [8] | Chen J, Song B, Mark R, Moeur M, Bible K (2004) Spatial relationship of biomass and species distribution in an old-growth Pseudotauga-Tsuga forest. Forest Science, 50, 364-376. |
| [9] | Chen J, Bradshaw GA (1999) Forest structure in space: a case study of an old growth spruce-fir forest in Changbaishan Natural Reserve, PR China. Forest Ecology and Management, 120, 205-215. |
| [10] | Clark DB, Clark DA, Rich PM, Weiss S (1996) Landscape-scale analyses of forest structure and understory light environments in a neotropical lowland rain forest. Canadian Journal of Forest Research, 26, 747-757. |
| [11] | Cormack RM, Ord JK (1979) Spatial and Temporal Analysis in Ecology. International Co-operative Publishing House, Fairland. |
| [12] | Gimaret-Carpentier C, Dray S, Pascal JP (2003) Broad-scale biodiversity pattern of the endemic tree flora of the Western Ghats (India) using canonical correlation analysis of herbarium records. Ecography, 26, 429-444. |
| [13] | Gittins R (1968) Trend-surface analysis of ecological data. Journal of Ecology, 56, 845-869. |
| [14] | Gittins R (1985) Canonical Analysis, A Review with Applications in Ecology. Springer-Verlag, Berlin. |
| [15] | Legendre P (1993) Spatial autocorrelation: trouble or new paradigm? Ecology, 74, 1659-1673. |
| [16] | Legendre P, Fortin MJ (1989) Spatial pattern and ecological analysis. Vegetatio, 80, 107-138. |
| [17] | Legendre P, Legendre L (1998) Numerical Ecology, 2nd edn. Elsevier Science, Amsterdam. |
| [18] | Méot A, Legendre P, Borcard D (1998) Partialling out the spatial component of ecological variation: questions and propositions in the linear modelling framework. Environmental and Ecological Statistics, 5, 1-27. |
| [19] | Michael AB, Robert JM, Paul PM, Stephen DP (2003) Light transmittance estimates in a longleaf pine woodland. Forest Science, 49, 752-762. |
| [20] | Norcliffe GB (1969) On the use and limitations of trend surface models. Canadian Geographer, 13, 338-348. |
| [21] | O’Neill RV, King AW(1998) Why are there so many books on scale? In: Ecological Scale—Theory and Applications (eds Peterson DL, Parker VT), pp. 3-15. Columbia University Press, New York. |
| [22] |
Olden JD, Jackson DA, Peres-Neto PR (2001) Spatial isolation and fish communities in drainage lakes. Oecologia, 127, 572-585.
DOI URL PMID |
| [23] | Pélissier R (1998) Tree spatial patterns in three contrasting plots in a southern Indian tropical moist evergreen forest. Journal of Tropical Ecology, 14, 1-16. |
| [24] | Pélissier R, Dray S, Sabatier D (2002) Within-plot relationships between tree species occurrences and hydrological soil constraints: an example in French Guiana investigated through canonical correlation analysis. Plant Ecology, 162, 143-156. |
| [25] | Peres-Neto PR (2004) Patterns in the co-occurrence of fish species in streams: the role of site suitability, morphology and phylogeny versus species interactions. Oecologia, 140, 352-360. |
| [26] | Roxburgh SH, Matsuki M (1999) The statistical validation of null models used in spatial association analyses. Oikos, 85, 68-78. |
| [27] | Scarlett MJ (1972) Problems of analysis of spatial distribution. In: Congrès International de Géographie (eds Adams WP, Helleiner FM), pp. 928-931, University of Toronto Press, Montréal. |
| [28] |
Selmi S, Boulinier T (2001) Ecological biogeography of southern ocean islands: the importance of considering spatial issues. The American Naturalist, 158, 426-437.
URL PMID |
| [29] | Shi HJ, Zhang LJ, Liu JG (2006) A new spatial-attribute weighting function for geographically weighted regression. Canadian Journal of Forest Research, 36, 996-1006. |
| [30] | Smith EP (2002) Ecological statistics. In: Encyclopedia of Environmetrics (eds El-Shaarawi AH, Piergorsch WW), pp. 589-602, John Wiley and Sons, Chichester. |
| [31] | Smith TM, Urban DL (1988) Scale and resolution of forest structural pattern. Vegetatio, 74, 143-150. |
| [32] | Sokal RR (1979) Testing statistical significance of geographic variation patterns. Systematic Zoology, 28, 227-232. |
| [33] | Student (1914) The elimination of spurious correlation due to position in time or space. Biometrika, 10, 179-180. |
| [34] | Wagner HH (2003) Spatial covariance in plant communities: integrating ordination, geostatistics, and variance testing. Ecology, 84, 1045-1057. |
| [35] | Wagner HH (2004) Direct multi-scale ordination with canonical correspondence analysis. Ecology, 85, 342-351. |
| [36] | Wartenberg D (1985) Canonical trend surface analysis: a method for describing geographic pattern. Systematic Zoology, 34, 259-279. |
| [37] | White PS, Miller RI (1988) Topographic models of vascular plant richness in the southern Appalachian peaks. Journal of Ecology, 76, 192-199. |
| [38] | Xiao DN (肖笃宁), Bu RC (布仁仓), Li XZ (李秀珍) (1997) Spatial ecology and landscape heterogeneity. Acta Ecologica Sinica (生态学报), 17, 453-461. (in Chinese with English abstract) |
| [1] | 苏荣菲, 陈睿山, 俞霖琳, 吴婧彬, 康燕. 基于红外相机调查的上海市长宁区社区生境花园生物多样性[J]. 生物多样性, 2024, 32(8): 24068-. |
| [2] | 施国杉, 刘峰, 曹光宏, 陈典, 夏尚文, 邓云, 王彬, 杨效东, 林露湘. 西双版纳热带季节雨林木本植物的beta多样性: 空间、环境与林分结构的作用[J]. 生物多样性, 2024, 32(12): 24285-. |
| [3] | 苏荣菲, 陈睿山, 郭晓娜. 城市社区更新中生物多样性的保护策略: 以上海市长宁区生境花园为例[J]. 生物多样性, 2023, 31(7): 23118-. |
| [4] | 李世东. 中国和美国国家公园时空发展及驱动因素[J]. 生物多样性, 2023, 31(6): 23040-. |
| [5] | 陈宏, 冼晓青, 陈宜雪, 林娜, 王苗苗, 李志鹏, 赵健. 海岛型城市红火蚁发生程度空间格局及驱动因子——以福建海坛岛为例[J]. 生物多样性, 2023, 31(5): 22501-. |
| [6] | 黄雨菲, 路春燕, 贾明明, 王自立, 苏越, 苏艳琳. 基于无人机影像与面向对象-深度学习的滨海湿地植物物种分类[J]. 生物多样性, 2023, 31(3): 22411-. |
| [7] | 张伟, 翟东东, 熊飞, 刘红艳, 陈元元, 王莹, 廖传松, 段辛斌, 田辉伍, 邓华堂, 陈大庆. 三峡库区鱼类群落结构和功能多样性[J]. 生物多样性, 2023, 31(2): 22136-. |
| [8] | 杨欣, 姚志良, 王彬, 温韩东, 邓云, 曹敏, 张志明, 谭正洪, 林露湘. 亚热带常绿阔叶林林分结构对物种组成变异的驱动作用: 从局域到区域尺度[J]. 生物多样性, 2023, 31(2): 22139-. |
| [9] | 田希, 刘文聪, 饶杰生, 王晓凤, 杨涛, 陈稀, 张秋雨, 刘其明, 徐衍潇, 张旭, 沈泽昊. 云南鸡足山半湿润常绿阔叶林的林隙干扰格局与成因[J]. 生物多样性, 2023, 31(11): 23219-. |
| [10] | 杨华林, 程跃红, 周天祥, 冯茜, 胡强, 张贵权, 杨建, 张晋东, 王彬, 周材权. 四川卧龙国家级自然保护区多空间尺度下绿尾虹雉的生境选择[J]. 生物多样性, 2022, 30(7): 21535-. |
| [11] | 付飞, 魏慧玉, 常育腾, 王备新, 陈凯. 澜沧江中游水生昆虫生活史和生态学性状多样性的海拔格局: 气候和土地利用的影响[J]. 生物多样性, 2022, 30(5): 21332-. |
| [12] | 孙佳欢, 刘冬, 朱家祺, 张书宁, 高梅香. 小麦-玉米轮作农田土壤螨多样性空间分布格局[J]. 生物多样性, 2022, 30(12): 22292-. |
| [13] | 井新, 蒋胜竞, 刘慧颖, 李昱, 贺金生. 气候变化与生物多样性之间的复杂关系和反馈机制[J]. 生物多样性, 2022, 30(10): 22462-. |
| [14] | 陈思淇, 张玉钧. 乡村景观生物多样性研究进展[J]. 生物多样性, 2021, 29(10): 1411-1424. |
| [15] | 魏慧玉,陈凯,王备新. 澜沧江流域水生昆虫群落分类多样性和功能多样性海拔格局的空间尺度依赖性[J]. 生物多样性, 2020, 28(4): 504-514. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
备案号:京ICP备16067583号-7
Copyright © 2026 版权所有 《生物多样性》编辑部
地址: 北京香山南辛村20号, 邮编:100093
电话: 010-62836137, 62836665 E-mail: biodiversity@ibcas.ac.cn
![]()