



生物多样性 ›› 2023, Vol. 31 ›› Issue (12): 23299. DOI: 10.17520/biods.2023299 cstr: 32101.14.biods.2023299
收稿日期:2023-08-24
接受日期:2023-12-11
出版日期:2023-12-20
发布日期:2023-12-30
通讯作者:
E-mail: 基金资助:
De Gao1,2( ), Yanping Wang1,*(
), Yanping Wang1,*( )(
)( )
)
Received:2023-08-24
Accepted:2023-12-11
Online:2023-12-20
Published:2023-12-30
Contact:
E-mail: 摘要:
小岛屿效应(small-island effect, SIE)描述了种-面积关系(species-area relationship, SAR)的一种特殊现象: 在面积低于某个阈值时, 物种数不随岛屿面积的增加而增加或以一种比大岛屿低的速率增加的现象。由于小岛屿效应的面积阈值可能是多种生物地理格局和生态学过程在空间尺度上的转折点, 另外该现象在生物多样性保护领域具有重要指导意义, 因此小岛屿效应已经成为岛屿生物地理学和生物多样性研究领域的一种重要格局。目前主要有5种分析和检验小岛屿效应的方法, 包括种-面积关系形状比较法(SAR shape comparison)、断点回归法(breakpoint/piecewise regression)、零模型法(null model)、路径分析法(path analysis)和树模型法(tree-based model)。本文首先简要介绍了小岛屿效应与种-面积关系的关联, 然后重点总结了文献中记载的小岛屿效应检测的5种方法的优点和不足。在SAR形状比较法中, 受大岛屿离群值效应的影响, SAR的形状往往很难呈现出“S”形曲线。在断点回归法中, 数据的对数转换使检测到的SIE可能只是一种假象。在零模型法中, 随机化过程忽略了物种之间生态特征的差异, 降低了岛屿物种丰富度预期值的可信度。在路径分析法中, 生境多样性难以量化以及SIE范围内如果SAR具有斜率则会降低该方法的适用性。在树模型法中, 如果面积不是物种丰富度变异的最佳预测因子, 树模型不会首先选择面积对样本进行拆分; 另外如果SAR存在两个面积阈值, 树模型可能不会从SIE阈值处进行拆分。因此, 为了避免因某种方法的自身不足而造成的错误判断, 我们建议: 首先应同时使用多种方法来进行SIE检测, 当至少有两种方法同时检测出SIE时, 方可认为系统中存在SIE; 其次, 针对现有检测方法中存在的缺陷加以改进也是今后重要的发展方向。最后, 本文针对国内学者从事较多的生境岛屿中SIE的特征以及导致全球变化的人类活动如何影响SIE的出现等问题给出了一些启发性建议。本文将为小岛屿效应的准确检测提供参考依据并为完善小岛屿效应的理论框架起到推动作用。
高德, 王彦平 (2023) 小岛屿效应检测方法研究进展. 生物多样性, 31, 23299. DOI: 10.17520/biods.2023299.
De Gao, Yanping Wang (2023) A review of the small-island effect detection methods and method advancement. Biodiversity Science, 31, 23299. DOI: 10.17520/biods.2023299.
| 模型形状 Model shape | 模型 Model | 公式 Equation1 | 参数数量 Number of parameters |
|---|---|---|---|
| 直线形 Linear shape | 线性模型 Linear | S = c + z × A | 2 |
| “C”形 Convex shape | 渐近模型 Asymptotic | S = d − c × z^A | 3 |
| “C”形 Convex shape | 对数模型 Logarithmic | S = c + z × log(A) | 2 |
| “C”形 Convex shape | 小林模型 Kobayashi | S = c × log(1 + A/z) | 2 |
| “C”形 Convex shape | 莫诺模型 Monod | S = d/(1 + c × A^(−1)) | 2 |
| “C”形 Convex shape | 负指数模型 Negative exponential | S = d × (1 − exp(−z × A)) | 2 |
| “C”形 Convex shape | 持久性函数1模型 Persistence function 1 | S = c × A^z × exp(−d × A) | 3 |
| “C”形 Convex shape | 幂函数模型 Power | S = c × A^z | 2 |
| “C”形 Convex shape | 罗森茨魏格幂函数模型 Power Rosenzweig | S = f + c × A^z | 3 |
| “C”形 Convex shape | 有理函数模型 Rational | S = (c + z × A)/(1 + d × A) | 3 |
| “S”形 Sigmoidal shape | 扩展幂函数2模型 Extended power 2 | S = c × A^(z − (d/A)) | 3 |
| “S”形 Sigmoidal shape | 冈珀茨模型 Gompertz | S = d × exp(−exp(−z × (A − c))) | 3 |
| “S”形 Sigmoidal shape | 逻辑斯蒂模型 Logistic | S = c/(f + A^(−z)) | 3 |
| “S”形 Sigmoidal shape | 摩根-默瑟-弗洛丁模型 Morgan-Mercer-Flodin | S = d/(1 + c × A^(−z)) | 3 |
| “S”形 Sigmoidal shape | 持久性函数2模型 Persistence function 2 | S = c × A^z × exp(−d/A) | 3 |
| “S”形 Sigmoidal shape | 威布尔-3模型 Weibull-3 | S = d × (1 − exp(−c × A^z)) | 3 |
| “S”形 Sigmoidal shape | 威布尔-4模型 Weibull-4 | S = d × (1 − exp(−c × A^z))^f | 4 |
| “S”形 Sigmoidal shape | Beta-P模型 Beta-P | S = d × (1 − (1 + (A/c)^z)^(−f)) | 4 |
| “S”形 Sigmoidal shape | 查普曼-理查兹模型 Chapman-Richards | S = d × (1 − exp(−z × A)^c) | 3 |
| “C”形或“S”形 Convex or sigmoidal shape | 扩展幂函数1模型 Extended power 1 | S = c × A^(z × A^(−d)) | 3 |
表1 sars程序包中提供的20种种-面积关系模型(修改自Matthews等, 2019)
Table 1 The 20 species-area relationship models available in the sars package (modified from Matthews et al, 2019)
| 模型形状 Model shape | 模型 Model | 公式 Equation1 | 参数数量 Number of parameters |
|---|---|---|---|
| 直线形 Linear shape | 线性模型 Linear | S = c + z × A | 2 |
| “C”形 Convex shape | 渐近模型 Asymptotic | S = d − c × z^A | 3 |
| “C”形 Convex shape | 对数模型 Logarithmic | S = c + z × log(A) | 2 |
| “C”形 Convex shape | 小林模型 Kobayashi | S = c × log(1 + A/z) | 2 |
| “C”形 Convex shape | 莫诺模型 Monod | S = d/(1 + c × A^(−1)) | 2 |
| “C”形 Convex shape | 负指数模型 Negative exponential | S = d × (1 − exp(−z × A)) | 2 |
| “C”形 Convex shape | 持久性函数1模型 Persistence function 1 | S = c × A^z × exp(−d × A) | 3 |
| “C”形 Convex shape | 幂函数模型 Power | S = c × A^z | 2 |
| “C”形 Convex shape | 罗森茨魏格幂函数模型 Power Rosenzweig | S = f + c × A^z | 3 |
| “C”形 Convex shape | 有理函数模型 Rational | S = (c + z × A)/(1 + d × A) | 3 |
| “S”形 Sigmoidal shape | 扩展幂函数2模型 Extended power 2 | S = c × A^(z − (d/A)) | 3 |
| “S”形 Sigmoidal shape | 冈珀茨模型 Gompertz | S = d × exp(−exp(−z × (A − c))) | 3 |
| “S”形 Sigmoidal shape | 逻辑斯蒂模型 Logistic | S = c/(f + A^(−z)) | 3 |
| “S”形 Sigmoidal shape | 摩根-默瑟-弗洛丁模型 Morgan-Mercer-Flodin | S = d/(1 + c × A^(−z)) | 3 |
| “S”形 Sigmoidal shape | 持久性函数2模型 Persistence function 2 | S = c × A^z × exp(−d/A) | 3 |
| “S”形 Sigmoidal shape | 威布尔-3模型 Weibull-3 | S = d × (1 − exp(−c × A^z)) | 3 |
| “S”形 Sigmoidal shape | 威布尔-4模型 Weibull-4 | S = d × (1 − exp(−c × A^z))^f | 4 |
| “S”形 Sigmoidal shape | Beta-P模型 Beta-P | S = d × (1 − (1 + (A/c)^z)^(−f)) | 4 |
| “S”形 Sigmoidal shape | 查普曼-理查兹模型 Chapman-Richards | S = d × (1 − exp(−z × A)^c) | 3 |
| “C”形或“S”形 Convex or sigmoidal shape | 扩展幂函数1模型 Extended power 1 | S = c × A^(z × A^(−d)) | 3 |
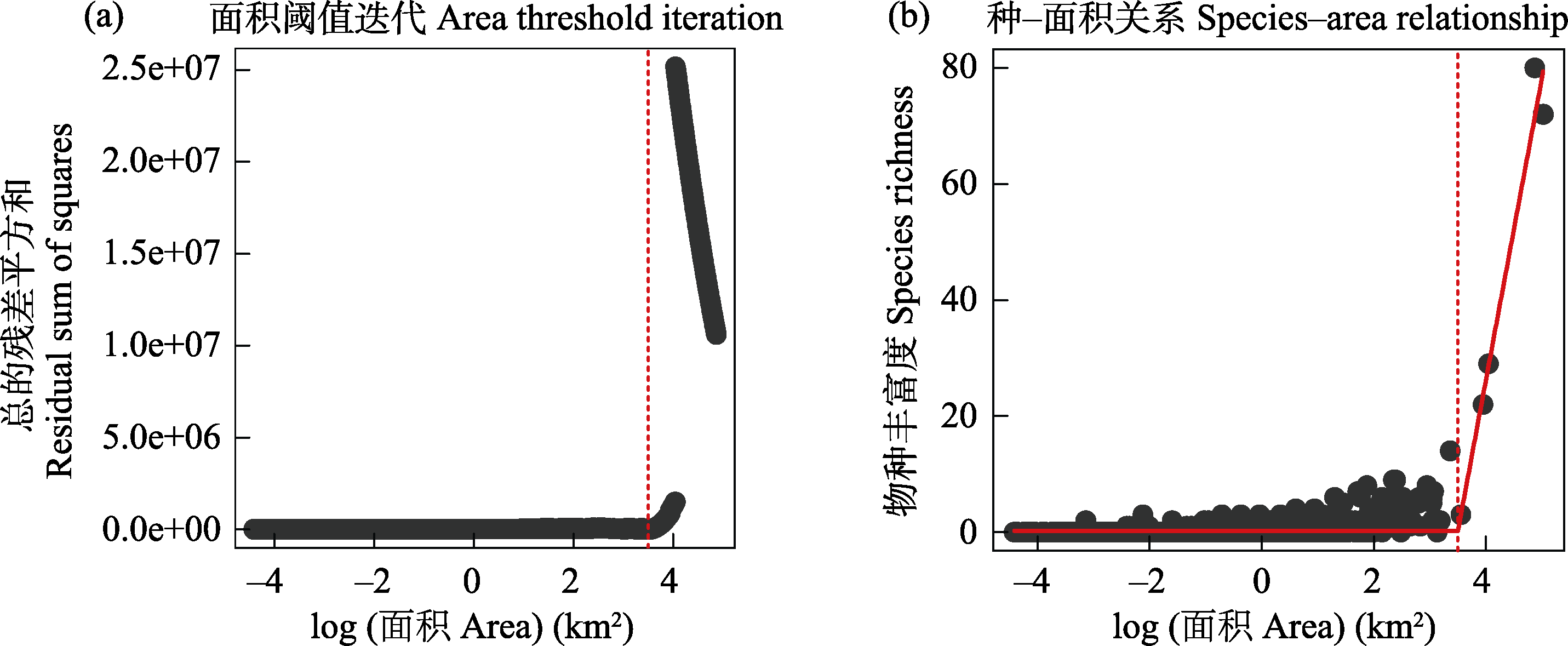
图2 使用Gao和Wang (2022)中第4个断点回归模型拟合西印度群岛两栖动物种-面积关系。(a)总的残差平方和随着面积阈值的迭代而变化; (b)种-面积关系拟合结果。数据来源于附录1。
Fig. 2 Fitting the species-area relationship of amphibians of the West Indies using a two-segmented piecewise regression models with a flat slope within the area threshold (Model 4 in Gao & Wang, 2022). (a) The residual sum of squares varies with the iteration of the area threshold; (b) Fitting results of the species-area relationship. The data used for analysis are from Appendix 1.
| 模型 Model | 公式 Equation1 | 片段数量 Number of segments |
|---|---|---|
| 1 | Y = c1 + (log A ≤ T1) z1 log A + (log A > T1) [z1 T1 + z2 (log A - T1)] | 2 |
| 2 | Y = c1 + (log A ≤ T1) [z1 log A + (z2 - z1) T1] + (log A > T1) z2 log A | 2 |
| 3 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1) (c2 + z2 log A) | 2 |
| 4 | Y = c1 + (log A > T1) z1 (log A - T1) | 2 |
| 5 | Y = c1 + (log A ≤ T1) z1 T1 + (log A > T1) z1 log A | 2 |
| 6 | Y = (log A ≤ T1) c1 + (log A > T1) (c2 + z1 log A) | 2 |
| 7 | Y = c1 + (log A ≤ T1) z1 log A + (log A > T1) z1 T1 | 2 |
| 8 | Y = c1 + (log A ≤ T1) z1 (log A - T1) | 2 |
| 9 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1) c2 | 2 |
| 10 | Y = (log A ≤ T2) [c1 + (log A ≤ T1) z1 T1 + (log A > T1) z1 log A] + (log A > T2) (c2 + z2 log A) | 3 |
| 11 | Y = (log A ≤ T1) c1 + (log A > T1 AND log A ≤ T2) (c2 + z1 log A) + (log A > T2) (c3 + z2 log A) | 3 |
| 12 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1 AND log A ≤ T2) (c2 + z2 log A) + (log A > T2) (c3 + z3 log A) | 3 |
| 13 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1 AND log A ≤ T2) (c2 + z2 log A) + (log A > T2) c3 | 3 |
| 14 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1 AND log A ≤ T2) [(c1 - c2 + z1 T1 - z2 T2) (log A - T1) / (T1 -T2) + c1 + z1 T1] + (log A > T2) (c2 + z2 log A) | 3 |
表2 14种用来检验小岛屿效应的断点回归模型(整理自Gao等, 2019)
Table 2 The 14 piecewise models for the detection of the small-island effect (organized from Gao et al, 2019)
| 模型 Model | 公式 Equation1 | 片段数量 Number of segments |
|---|---|---|
| 1 | Y = c1 + (log A ≤ T1) z1 log A + (log A > T1) [z1 T1 + z2 (log A - T1)] | 2 |
| 2 | Y = c1 + (log A ≤ T1) [z1 log A + (z2 - z1) T1] + (log A > T1) z2 log A | 2 |
| 3 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1) (c2 + z2 log A) | 2 |
| 4 | Y = c1 + (log A > T1) z1 (log A - T1) | 2 |
| 5 | Y = c1 + (log A ≤ T1) z1 T1 + (log A > T1) z1 log A | 2 |
| 6 | Y = (log A ≤ T1) c1 + (log A > T1) (c2 + z1 log A) | 2 |
| 7 | Y = c1 + (log A ≤ T1) z1 log A + (log A > T1) z1 T1 | 2 |
| 8 | Y = c1 + (log A ≤ T1) z1 (log A - T1) | 2 |
| 9 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1) c2 | 2 |
| 10 | Y = (log A ≤ T2) [c1 + (log A ≤ T1) z1 T1 + (log A > T1) z1 log A] + (log A > T2) (c2 + z2 log A) | 3 |
| 11 | Y = (log A ≤ T1) c1 + (log A > T1 AND log A ≤ T2) (c2 + z1 log A) + (log A > T2) (c3 + z2 log A) | 3 |
| 12 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1 AND log A ≤ T2) (c2 + z2 log A) + (log A > T2) (c3 + z3 log A) | 3 |
| 13 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1 AND log A ≤ T2) (c2 + z2 log A) + (log A > T2) c3 | 3 |
| 14 | Y = (log A ≤ T1) (c1 + z1 log A) + (log A > T1 AND log A ≤ T2) [(c1 - c2 + z1 T1 - z2 T2) (log A - T1) / (T1 -T2) + c1 + z1 T1] + (log A > T2) (c2 + z2 log A) | 3 |
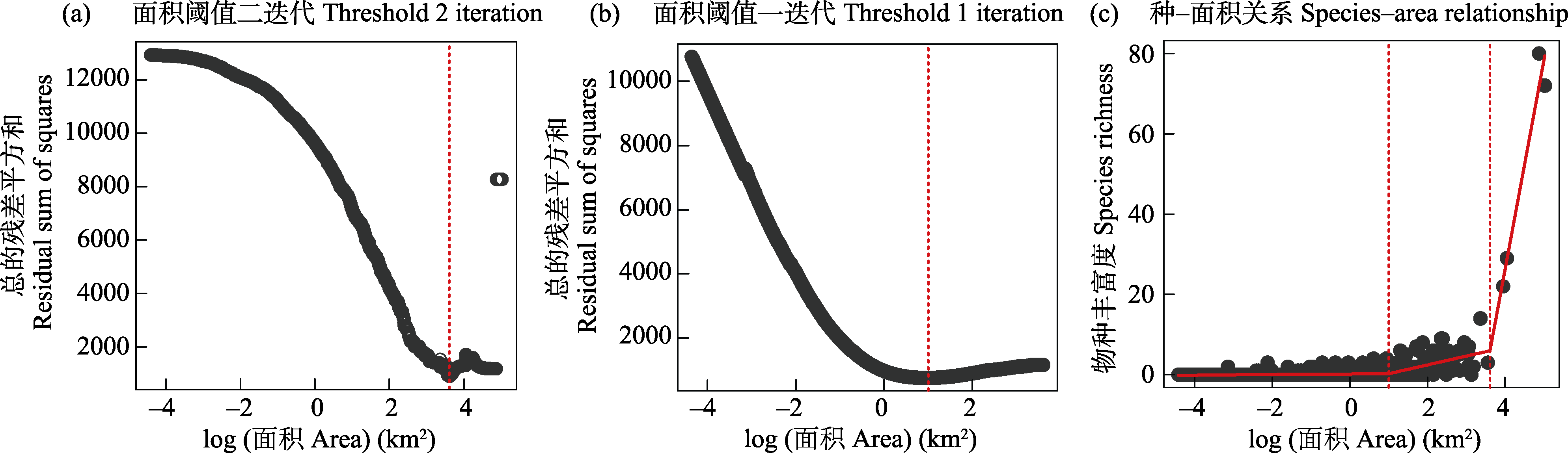
图3 使用Gao和Wang (2022)中第6个断点回归模型拟合西印度群岛两栖类种-面积关系。(a)总的残差平方和随着第二个面积阈值的迭代而变化; (b)总的残差平方和随着第一个面积阈值的迭代而变化; (c)种-面积关系拟合结果。数据来源于附录1。
Fig. 3 Fitting the species-area relationship of amphibians of the West Indies using a three-segmented piecewise regression model (Model 6 in Gao & Wang, 2022). (a) The residual sum of squares varies with the iteration of the second area threshold; (b) The residual sum of squares varies with the iteration of the first area threshold; (c) Fitting results of the species-area relationship. The data used for analysis are from Appendix 1.
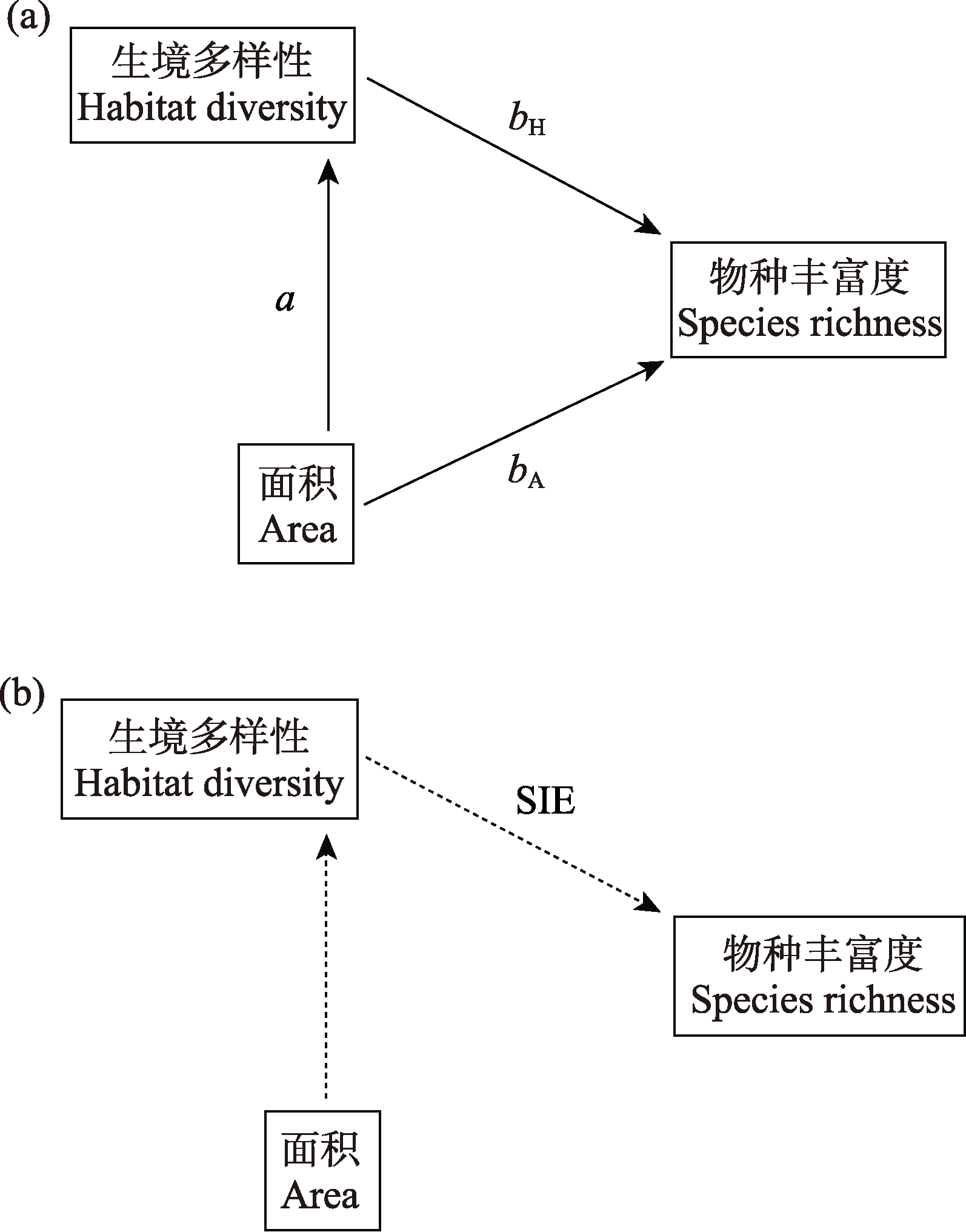
图4 参考Triantis等(2006)构建的面积和生境多样性对物种丰富度影响的结构方程模型。(a)在大岛屿上, 面积对物种丰富度既有直接影响又有间接影响; (b)在小岛屿上, 面积对物种丰富度的直接影响消失。a, bA, bH和SIE为标准回归系数。实线和虚线分别表示0.05水平下的显著效果和非显著效果。
Fig. 4 A structural equation model for the effects of area and habitat diversity on species richness according to Triantis et al, 2006. (a) On large islands, area has both direct and indirect impacts on species richness; (b) On small islands, the direct impact of area on species richness disappears. a, bA, bH, and SIE are standardized regression coefficients. Solid and dashed lines represent the significant and non-significant effects at the 0.05 level respectively.
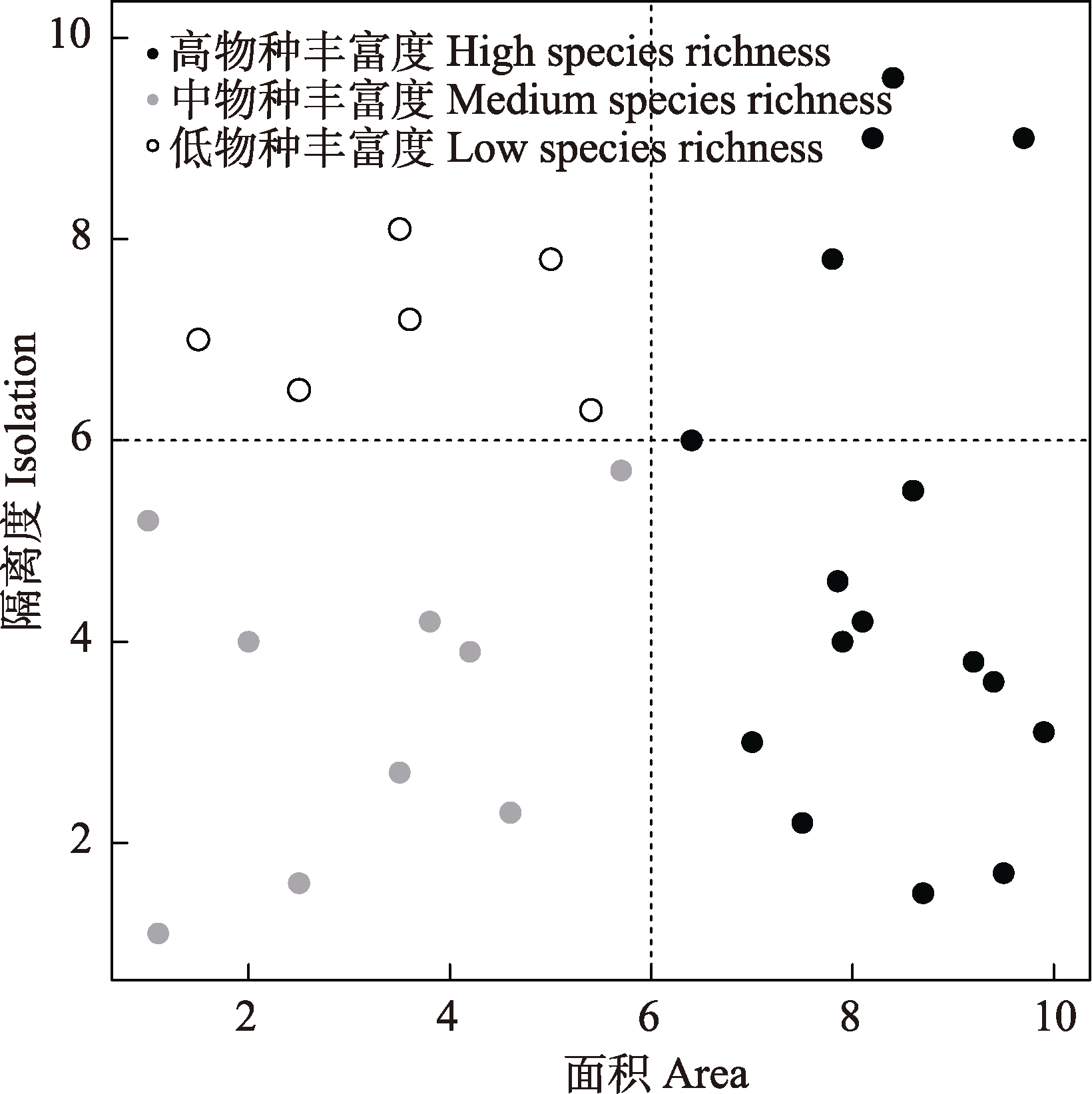
图5 使用岛屿面积和岛屿隔离度两个自变量来预测物种丰富度并绘制散点图
Fig. 5 Using two independent variables, island area and island isolation, to predict species richness and make scatter plot
| 属性 Attribute | 种-面积关系形状比较法 SAR shape comparison | 断点回归法Breakpoint/piecewise regression | 零模型法Null model | 路径分析法Path analysis | 树模型法Tree-based model |
|---|---|---|---|---|---|
| 能否计算SIE面积阈值 Whether being able to calculate the SIE area threshold | 否 No | 是 Yes | 否 No | 是 Yes | 是 Yes |
| 能否判断SIE区间内SAR具有斜率 Whether being able to determine SAR slope within the limit of the SIE | 否 No | 是 Yes | 否 No | 否 No | 否 No |
| 是否只依赖岛屿面积和物种丰富度数据 Whether only relying on island area and species richness data | 是 Yes | 是 Yes | 是 Yes | 否 No | 否 No |
| 是否必须将岛屿面积对数转化 Whether logarithmic transformation is required for island area | 否 No | 是 Yes | 否 No | 否 No | 否 No |
| 犯I类错误的概率 Probability of making type I error1 | 低 Low | 高 High | 低 Low | 低 Low | 低 Low |
| 犯II类错误的概率 Probability of making type II error2 | 高 High | 低 Low | 低 Low | 高 High | 高 High |
| 使用这5种SIE检测方法的论文数 Number of publications using the five SIE detection methods | 5 | 45 | 4 | 9 | 1 |
表3 5种小岛屿效应检测方法的属性比较
Table 3 Attribute comparison among the five small-island effect (SIE) detection methods
| 属性 Attribute | 种-面积关系形状比较法 SAR shape comparison | 断点回归法Breakpoint/piecewise regression | 零模型法Null model | 路径分析法Path analysis | 树模型法Tree-based model |
|---|---|---|---|---|---|
| 能否计算SIE面积阈值 Whether being able to calculate the SIE area threshold | 否 No | 是 Yes | 否 No | 是 Yes | 是 Yes |
| 能否判断SIE区间内SAR具有斜率 Whether being able to determine SAR slope within the limit of the SIE | 否 No | 是 Yes | 否 No | 否 No | 否 No |
| 是否只依赖岛屿面积和物种丰富度数据 Whether only relying on island area and species richness data | 是 Yes | 是 Yes | 是 Yes | 否 No | 否 No |
| 是否必须将岛屿面积对数转化 Whether logarithmic transformation is required for island area | 否 No | 是 Yes | 否 No | 否 No | 否 No |
| 犯I类错误的概率 Probability of making type I error1 | 低 Low | 高 High | 低 Low | 低 Low | 低 Low |
| 犯II类错误的概率 Probability of making type II error2 | 高 High | 低 Low | 低 Low | 高 High | 高 High |
| 使用这5种SIE检测方法的论文数 Number of publications using the five SIE detection methods | 5 | 45 | 4 | 9 | 1 |
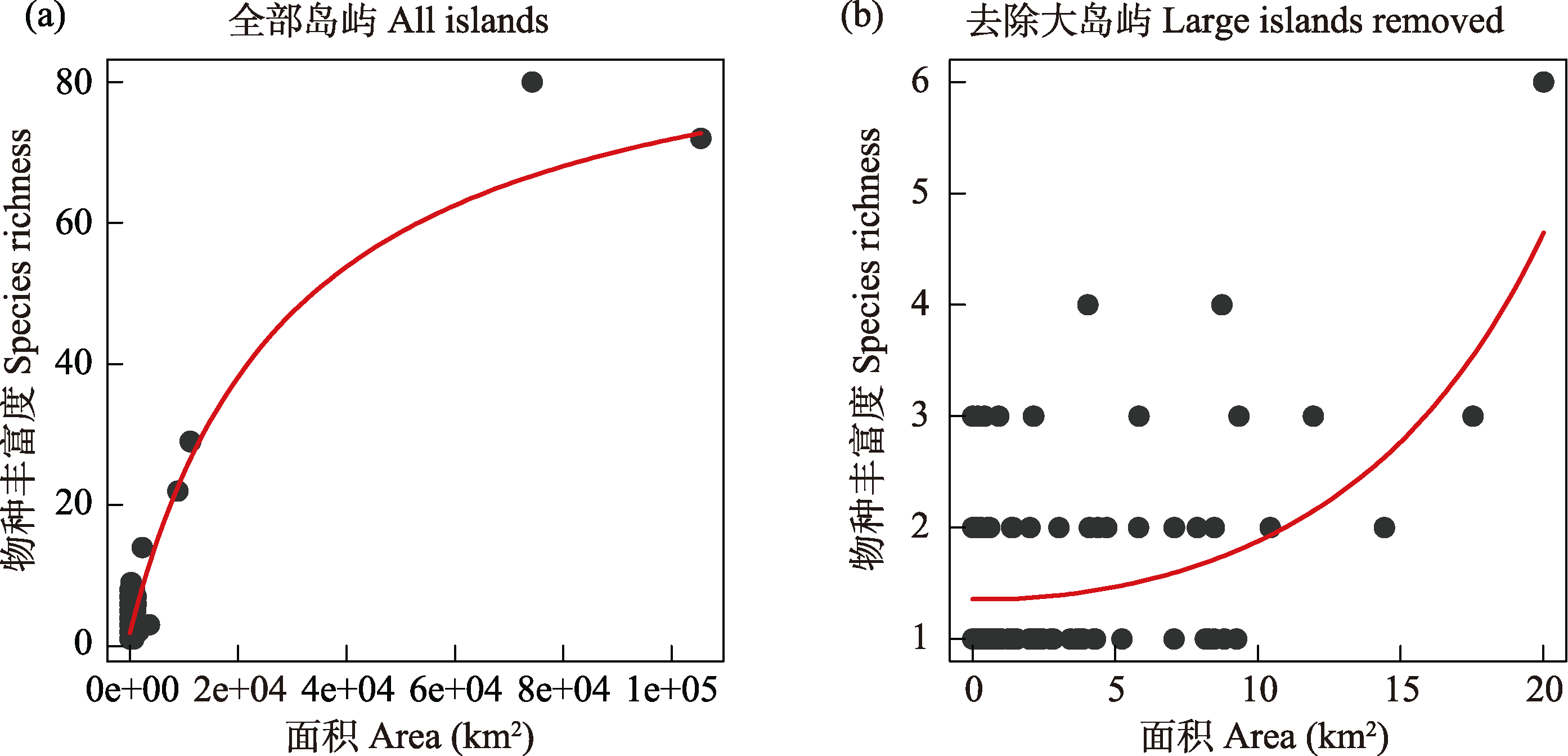
图7 西印度群岛两栖动物种-面积关系。(a)全部166个两栖类出现的岛屿; (b)从全部两栖类出现的岛屿中删除了前40%的大岛屿。数据来源于附录1。
Fig. 7 The species-area relationship of amphibians of the West Indies. (a) All amphibian-inhabited islands; (b) Removing the top 40% of large islands from all amphibian-inhabited islands. The data used for analysis are from Appendix 1.
| [1] |
Arrhenius O (1921) Species and area. Journal of Ecology, 9, 95-99.
DOI URL |
| [2] | Burnham KP, Anderson DR (2002) Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Springer, New York. |
| [3] |
Burns KC, McHardy PR, Pledger S (2009) The small-island effect: Fact or artefact? Ecography, 32, 269-276.
DOI URL |
| [4] |
Chen CW, Xu AC, Wang YP (2021) Area threshold and trait-environment associations of butterfly assemblages in the Zhoushan Archipelago, China. Journal of Biogeography, 48, 785-797.
DOI URL |
| [5] |
Chen CW, Yang XR, Tan XW, Wang YP (2020) The role of habitat diversity in generating the small-island effect. Ecography, 43, 1241-1249.
DOI URL |
| [6] |
Connor EF, McCoy ED (1979) The statistics and biology of the species-area relationship. The American Naturalist, 113, 791-833.
DOI URL |
| [7] |
De’ath G, Fabricius KE (2000) Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology, 81, 3178-3192.
DOI URL |
| [8] |
Dengler J (2010) Robust methods for detecting a small island effect. Diversity and Distributions, 16, 256-266.
DOI URL |
| [9] |
Dengler J, Matthews TJ, Steinbauer MJ, Wolfrum S, Boch S, Chiarucci A, Conradi T, Dembicz I, Marcenò C, García‐Mijangos I, Nowak A, Storch D, Ulrich W, Campos JA, Cancellieri L, Carboni M, Ciaschetti G, De Frenne P, Dolezal J, Dolnik C, Essl F, Fantinato E, Filibeck G, Grytnes J-A, Guarino R, Güler B, Janišová M, Klichowska E, Kozub Ł, Kuzemko A, Manthey M, Mimet A, Naqinezhad A, Pedersen C, Peet RK, Pellissier V, Pielech R, Potenza G, Rosati L, Terzi M, Valkó O, Vynokurov D, White H, Winkler M, Biurrun I (2020) Species-area relationships in continuous vegetation: Evidence from Palaearctic grasslands. Journal of Biogeography, 47, 72-86.
DOI URL |
| [10] |
Drakare S, Lennon JJ, Hillebrand H (2006) The imprint of the geographical, evolutionary and ecological context on species-area relationships. Ecology Letters, 9, 215-227.
DOI PMID |
| [11] |
Fattorini S (2007) To fit or not to fit? A poorly fitting procedure produces inconsistent results when the species-area relationship is used to locate hotspots. Biodiversity and Conservation, 16, 2531-2538.
DOI URL |
| [12] | Forster G (1777) A voyage around the world in his Majesty’s sloop, resolution, commanded by Captain James Cook, during the years 1772, 3, 4, and 5. B. Volume 1. White B, Robson J, Elmsly P, Robinson G, London. |
| [13] | Forster JR (1778) Observations made During a Voyage Round the World. Robinson G, London. |
| [14] |
Gao D, Cao Z, Xu P, Perry G (2019) On piecewise models and species-area patterns. Ecology and Evolution, 9, 8351-8361.
DOI |
| [15] |
Gao D, Perry G (2016) Detecting the small island effect and nestedness of herpetofauna of the West Indies. Ecology and Evolution, 6, 5390-5403.
DOI PMID |
| [16] | Gao D, Wang YP (2022) A global synthesis of the small-island effect in amphibians and reptiles. Ecography, 2022, e05957. |
| [17] |
Gao D, Wang YP (2024) Non-linear thresholds in the effect of area on three dimensions of diversity of herpetofauna in the West Indies. Journal of Biogeography, 51, 439-453.
DOI URL |
| [18] |
Gentile G, Argano R (2005) Island biogeography of the Mediterranean Sea: The species-area relationship for terrestrial isopods. Journal of Biogeography, 32, 1715-1726.
DOI URL |
| [19] | Gilpin ME, Diamond JM (1976) Calculation of immigration and extinction curves from the species-area-distance relation. Proceedings of the National Academy of Sciences, USA, 73, 4130-4134. |
| [20] |
Guilhaumon F, Mouillot D, Gimenez O (2010) mmSAR: An R-package for multimodel species-area relationship inference. Ecography, 33, 420-424.
DOI URL |
| [21] |
Harcourt AH, Doherty DA (2005) Species-area relationships of primates in tropical forest fragments: A global analysis. Journal of Applied Ecology, 42, 630-637.
DOI URL |
| [22] | He F, Legendre P (2002) Species diversity patterns derived from species-area models. Ecology, 83, 1185-1198. |
| [23] | Henderson RW, Powell R (2001) Responses by the West Indian herpetofauna to human-influenced resources. Caribbean Journal of Science, 37, 41-54. |
| [24] | Hubbell SP (2001) The Unified Neutral Theory of Biodiversity and Biogeography. Princeton University Press, Princeton, NJ. |
| [25] |
Lomolino MV (2000) Ecology’s most general, yet protean pattern: The species-area relationship. Journal of Biogeography, 27, 17-26.
DOI URL |
| [26] |
Lomolino MV, Weiser MD (2001) Towards a more general species-area relationship: Diversity on all islands, great and small. Journal of Biogeography, 28, 431-445.
DOI URL |
| [27] | MacArthur RH, Wilson EO (1967) The Theory of Island Biogeography. Princeton University Press, Princeton, NJ. |
| [28] | Matthews TJ, Rigal F (2021) Thresholds and the species-area relationship: A set of functions for fitting, evaluating and plotting a range of commonly used piecewise models in R. Frontiers of Biogeography, 13, e49404. |
| [29] |
Matthews TJ, Rigal F, Kougioumoutzis K, Trigas P, Triantis KA (2020) Unravelling the small-island effect through phylogenetic community ecology. Journal of Biogeography, 47, 2341-2352.
DOI URL |
| [30] |
Matthews TJ, Triantis KA, Whittaker RJ, Guihaumon F (2019) sar: An R package for fitting, evaluating and comparing species-area relationship models. Ecography, 42, 1446-1455.
DOI |
| [31] |
Menegotto A, Rangel TF, Schrader J, Weigelt P, Kreft H (2020) A global test of the subsidized island biogeography hypothesis. Global Ecology and Biogeography, 29, 320-330.
DOI |
| [32] |
Morrison LW (2014) The small-island effect: Empty islands, temporal variability and the importance of species composition. Journal of Biogeography, 41, 1007-1017.
DOI URL |
| [33] | Muggeo VMR (2008) Segmented: An R package to fit regression models with broken-line relationships. R News, 8, 20-25. |
| [34] |
Neigel JE (2003) Species-area relationships and marine conservation. Ecological Applications, 13, 138-145.
DOI URL |
| [35] |
Niering WA (1963) Terrestrial ecology of Kapingamarangi atoll, Caroline Islands. Ecological Monographs, 33, 131-160.
DOI URL |
| [36] |
Qie L, Lee TM, Sodhi NS, Lim SLH (2011) Dung beetle assemblages on tropical land-bridge islands: Small island effect and vulnerable species. Journal of Biogeography, 38, 792-804.
DOI URL |
| [37] | Raxworthy CJ, Nussbaum RA (2000) Extinction and extinction vulnerability of amphibians and reptiles in Madagascar. Amphibian and Reptile Conservation, 2, 15-23. |
| [38] | Rosenzweig ML (1995) Species Diversity in Space and Time. Cambridge University Press, Cambridge. |
| [39] | Rosenzweig ML (2004) Applying species-area relationships to the conservation of diversity. In: Frontiers of Biogeography: New Directions in the Geography of Nature (eds Lomolino MV, Heaney LR), pp. 325-343. Sinauer Associates, Sunderland, MA. |
| [40] |
Rosindell J, Cornell SJ (2009) Species-area curves, neutral models, and long-distance dispersal. Ecology, 90, 1743-1750.
DOI PMID |
| [41] |
Schrader J, König C, Triantis KA, Trigas P, Kreft H, Weigelt P (2020) Species-area relationships on small islands differ among plant growth forms. Global Ecology and Biogeography, 29, 814-829.
DOI URL |
| [42] |
Schrader J, Moeljono S, Keppel G, Kreft H (2019) Plants on small islands revisited: The effects of spatial scale and habitat quality on the species-area relationship. Ecography, 42, 1405-1414.
DOI |
| [43] |
Sfenthourakis S (1996) The species-area relationship of terrestrial isopods (Isopoda; Oniscidea) from the Aegean Archipelago (Greece): A comparative study. Global Ecology and Biogeography Letters, 5, 149-157.
DOI URL |
| [44] |
Sfenthourakis S, Triantis KA, Proios K, Rigal F (2021) The role of ecological specialization in shaping patterns of insular communities. Journal of Biogeography, 48, 243-252.
DOI URL |
| [45] | Sonderegger D (2020) SiZer: Significant Zero Crossings. R package version 0.1-7. https://CRAN.R-project.org/package=SiZer. (accessed on 2022-07-09) |
| [46] |
Stark SC, Bunker DE, Carson WP (2006) A null model of exotic plant diversity tested with exotic and native species-area relationships. Ecology Letters, 9, 136-141.
PMID |
| [47] |
Tjørve E (2003) Shapes and functions of species-area curves: A review of possible models. Journal of Biogeography, 30, 827-835.
DOI URL |
| [48] |
I) A review of new models and parameterizations. Journal of Biogeography, 36, 1435-1445.
DOI URL |
| [49] |
Triantis KA, Guilhaumon F, Whittaker RJ (2012) The island species-area relationship: Biology and statistics. Journal of Biogeography, 39, 215-231.
DOI URL |
| [50] |
Triantis KA, Sfenthourakis S (2012) Island biogeography is not a single-variable discipline: The small island effect debate. Diversity and Distributions, 18, 92-96.
DOI URL |
| [51] |
Triantis KA, Vardinoyannis K, Tsolaki EP, Botsaris I, Lika K, Mylonas M (2006) Re-approaching the small island effect. Journal of Biogeography, 33, 914-923.
DOI URL |
| [52] | von Humboldt A (1807) Ideen zur einer Geographie der Pflanstzen nebst einem Naturgemälde der Tropenländer, Cotta, Tübringen. |
| [53] | Wang YP, Chen CW, Millien V (2018) A global synthesis of the small-island effect in habitat islands. Proceedings of the Royal Society B: Biological Sciences, 285, 20181868. |
| [54] |
Wang YP, Chen CW, Millien V (2023) The integration of the small‐island effect and nestedness pattern. Journal of Biogeography, 50, 1234-1243.
DOI URL |
| [55] |
Wang YP, Millien V, Ding P (2016) On empty islands and the small-island effect. Global Ecology and Biogeography, 25, 1333-1345.
DOI URL |
| [56] |
Wang YP, Wu Q, Wang X, Liu C, Wu LB, Chen CW, Ge DP, Song X, Chen CS, Xu AC, Ding P (2015) Small-island effect in snake communities on islands of an inundated lake: The need to include zeroes. Basic and Applied Ecology, 16, 19-27.
DOI URL |
| [57] |
Wang YP, Zhang M, Wang SY, Ding ZF, Zhang JC, Sun JJ, Li P, Ding P (2012) No evidence for the small island effect in avian communities on islands of an inundated lake. Oikos, 121, 1945-1952.
DOI URL |
| [58] |
Whitehead DR, Jones CE (1969) Small islands and the equilibrium theory of insular biogeography. Evolution, 23, 171-179.
DOI PMID |
| [59] | Whittaker RJ, Fernandez-Palacios JM (2007) Island Biogeography: Ecology, Evolution, and Conservation, 2nd edn. Oxford University Press, Oxford. |
| [60] | Wintle BA, Kujala H, Whitehead A, Cameron A, Veloz S, Kukkala A, Moilanen A, Gordon A, Lentini PE, Cadenhead NCR, Bekessy SA (2019) Global synthesis of conservation studies reveals the importance of small habitat patches for biodiversity. Proceedings of the National Academy of Sciences, USA, 116, 909-914. |
| [61] |
Yan YZ, Jarvie S, Zhang Q, Han P, Liu QF, Zhang SS, Liu PT (2023) Habitat heterogeneity determines species richness on small habitat islands in a fragmented landscape. Journal of Biogeography, 50, 976-986.
DOI URL |
| [62] |
Yan YZ, Jarvie S, Zhang Q, Zhang SS, Han P, Liu QF, Liu PT (2021) Small patches are hotspots for biodiversity conservation in fragmented landscapes. Ecological Indicators, 130, 108086.
DOI URL |
| [63] |
Yu J, Li DD, Zhang ZY, Guo SL (2020) Species-area relationship and small-island effect of bryophytes on the Zhoushan Archipelago, China. Journal of Biogeography, 47, 978-992.
DOI URL |
| [1] | 谢艳秋, 黄晖, 王春晓, 何雅琴, 江怡萱, 刘子琳, 邓传远, 郑郁善. 福建海岛滨海特有植物种-面积关系及物种丰富度决定因素[J]. 生物多样性, 2023, 31(5): 22345-. |
| [2] | 王彦平, 张敏楚, 詹成修. 嵌套分布格局研究进展: 分析方法、影响机制及保护应用[J]. 生物多样性, 2023, 31(12): 23314-. |
| [3] | 商晓凡, 张健, 高浩杰, 库伟鹏, 毕玉科, 李修鹏, 阎恩荣. 岛屿面积与气候共同影响舟山群岛种子植物丰富度格局[J]. 生物多样性, 2023, 31(12): 23392-. |
| [4] | 肖兰, 董标, 张琳婷, 邓传远, 李霞, 刘建辉, 吴端聪. 渤海区无居民海岛植物物种丰富度分布格局[J]. 生物多样性, 2022, 30(4): 21231-. |
| [5] | 秦运芝, 张佳鑫, 刘检明, 刘梦婷, 万丹, 吴浩, 周阳, 孟红杰, 肖之强, 黄汉东, 徐耀粘, 卢志军, 乔秀娟, 江明喜. 湖南八大公山25 ha常绿落叶阔叶混交林动态监测样地群落组成与空间结构[J]. 生物多样性, 2018, 26(9): 1016-1022. |
| [6] | 徐翔, 张化永, 谢婷, 孙青青, 田永兰. 西双版纳种子植物物种多样性的垂直格局及机制[J]. 生物多样性, 2018, 26(7): 678-689. |
| [7] | 斯幸峰, 赵郁豪, 陈传武, 任鹏, 曾頔, 吴玲兵, 丁平. Beta多样性分解: 方法、应用与展望[J]. 生物多样性, 2017, 25(5): 464-480. |
| [8] | 闫满玉, 杜晓军, 赵爱花, 彭明春. 河南宝天曼落叶阔叶林木本植物单物种-面积关系[J]. 生物多样性, 2015, 23(5): 630-640. |
| [9] | 仲磊, 张杨家豪, 卢品, 顾雪萍, 雷祖培, 蔡延奔, 郑方东, 孙义方, 于明坚. 次生常绿阔叶林的群落结构与物种组成:基于浙江乌岩岭9 ha森林动态样地[J]. 生物多样性, 2015, 23(5): 619-629. |
| [10] | 徐爱春, 斯幸峰, 王彦平, 丁平. 千岛湖片段化栖息地地栖哺乳动物的红外相机监测及最小监测时长[J]. 生物多样性, 2014, 22(6): 764-772. |
| [11] | 陈波, 包志毅. 城市公园和郊区公园生物多样性评估的指标[J]. 生物多样性, 2003, 11(2): 169-176. |
| [12] | 李义明, 李典谟. 自然保护区设计的主要原理和方法[J]. 生物多样性, 1996, 04(1): 32-40. |
| [13] | 李义明, 李典谟. 种群生存力分析研究进展和趋势[J]. 生物多样性, 1994, 02(1): 1-10. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
备案号:京ICP备16067583号-7
Copyright © 2026 版权所有 《生物多样性》编辑部
地址: 北京香山南辛村20号, 邮编:100093
电话: 010-62836137, 62836665 E-mail: biodiversity@ibcas.ac.cn
![]()