

|
|
||
|
SLOSS争论研究进展: 分析方法、理论机制及保护实践
生物多样性
2025, 33 (7):
25081-.
DOI: 10.17520/biods.2025081
生物多样性保护领域中的SLOSS (single large or several small)争论概述了在总面积相等或资源有限的情况下, 应该优先保护一个大的保护区(SL)还是几个小的保护区(SS)来最大化保护物种多样性的问题。自20世纪70年代以来, 该问题一直备受生态学家和保护生物学家的关注, 其研究对于保护区设计以及生物多样性保护具有重要意义。随着研究方法的发展和交叉学科的兴起, SLOSS争论在分析方法和理论机制方面都取得了重要的阶段性进展。本文通过文献检索和归纳总结对SLOSS争论的研究现状进行了综述。首先, 我们回顾了SLOSS争论的起源及其对生物多样性保护的重要性。其次, 本文概括评估了SLOSS争论在实证研究和理论方面的分析方法, 包括零模型法、经典的物种累积曲线法以及由该方法所计算出来的饱和指数。随后, 本文还回顾了以往研究者提出的改进的饱和指数, 并介绍了我们所开发的优化后的饱和指数。此外, 本文探讨了几种影响SLOSS争论的理论机制, 如由灭绝率和定殖率的变化所主导的灭绝-定殖动态理论机制及其相应的检验方法。最后, 本文对该领域进行了总结和展望并为未来的发展方向提出了一些针对性建议, 包括采用多种保护策略的重要性以及在保护区规划中经济和生态因素的结合的必要性。本文整合了SLOSS争论中常用的分析方法的适用场景与局限性, 比较了不同方法在划分保护优先级时的优势和争议点, 可为研究者在方法选择及保护规划权衡方面提供参考。 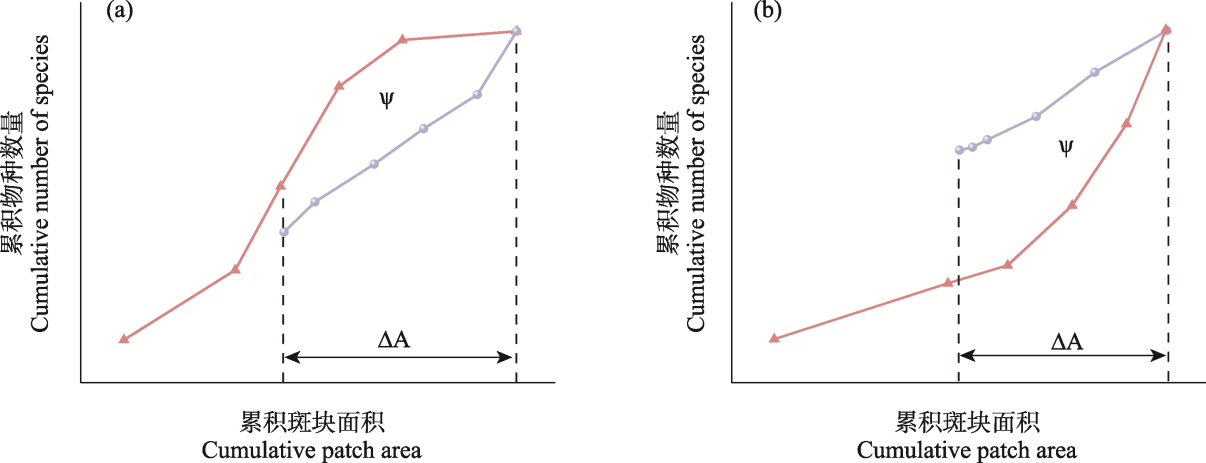 View image in article
图3
用于表征从小到大累积曲线(红色)和从大到小累积曲线(灰色)之间偏差的ξ统计量以及指标ΔA示意图。Ψ代表从最大斑块面积推导出的两条曲线下面积的差值; ΔA表示估算两个面积的区域范围。图(a)表示ξ统计量为正的情况, 图(b)代表ξ统计量为负的情况。
正文中引用本图/表的段落
Mac Nally和Lake (1999)注意到, SS和SL曲线下面积的计算均是从最小累积面积所对应的点开始, 并且SL曲线的下限对应于最大斑块的面积。其次, 两条曲线的上限是相同的, 也即所有斑块的总累积面积相等。因此, SL曲线下的面积主要依赖于最大斑块的面积。为了减轻这种依赖性, 他们建议从最大斑块的面积到所有斑块的总累积面积来计算区间内的积分。这些积分的差值代表图3中Ψ符号所示的面积。之后, 他们用Ψ除以两个积分的面积范围ΔA得到ξ统计量, 即ξ = Ψ/ΔA (图3)。ξ统计量表示SS曲线和SL曲线在ΔA区间内的累积丰富度加权的差异(Mac Nally & Lake, 1999)。若SS曲线位于SL曲线之上, 则ξ统计量为正, 表明几个小斑块的平均累积物种丰富度超过单个大的斑块, 若ξ统计量为负, 则为相反的情况(Mac Nally & Lake, 1999)。
本文的其它图/表
|