SLOSS争论研究进展: 分析方法、理论机制及保护实践
章洋, 王彦平
生物多样性
2025, 33 ( 7):
25081-.
DOI: 10.17520/biods.2025081
生物多样性保护领域中的SLOSS (single large or several small)争论概述了在总面积相等或资源有限的情况下, 应该优先保护一个大的保护区(SL)还是几个小的保护区(SS)来最大化保护物种多样性的问题。自20世纪70年代以来, 该问题一直备受生态学家和保护生物学家的关注, 其研究对于保护区设计以及生物多样性保护具有重要意义。随着研究方法的发展和交叉学科的兴起, SLOSS争论在分析方法和理论机制方面都取得了重要的阶段性进展。本文通过文献检索和归纳总结对SLOSS争论的研究现状进行了综述。首先, 我们回顾了SLOSS争论的起源及其对生物多样性保护的重要性。其次, 本文概括评估了SLOSS争论在实证研究和理论方面的分析方法, 包括零模型法、经典的物种累积曲线法以及由该方法所计算出来的饱和指数。随后, 本文还回顾了以往研究者提出的改进的饱和指数, 并介绍了我们所开发的优化后的饱和指数。此外, 本文探讨了几种影响SLOSS争论的理论机制, 如由灭绝率和定殖率的变化所主导的灭绝-定殖动态理论机制及其相应的检验方法。最后, 本文对该领域进行了总结和展望并为未来的发展方向提出了一些针对性建议, 包括采用多种保护策略的重要性以及在保护区规划中经济和生态因素的结合的必要性。本文整合了SLOSS争论中常用的分析方法的适用场景与局限性, 比较了不同方法在划分保护优先级时的优势和争议点, 可为研究者在方法选择及保护规划权衡方面提供参考。
View image in article
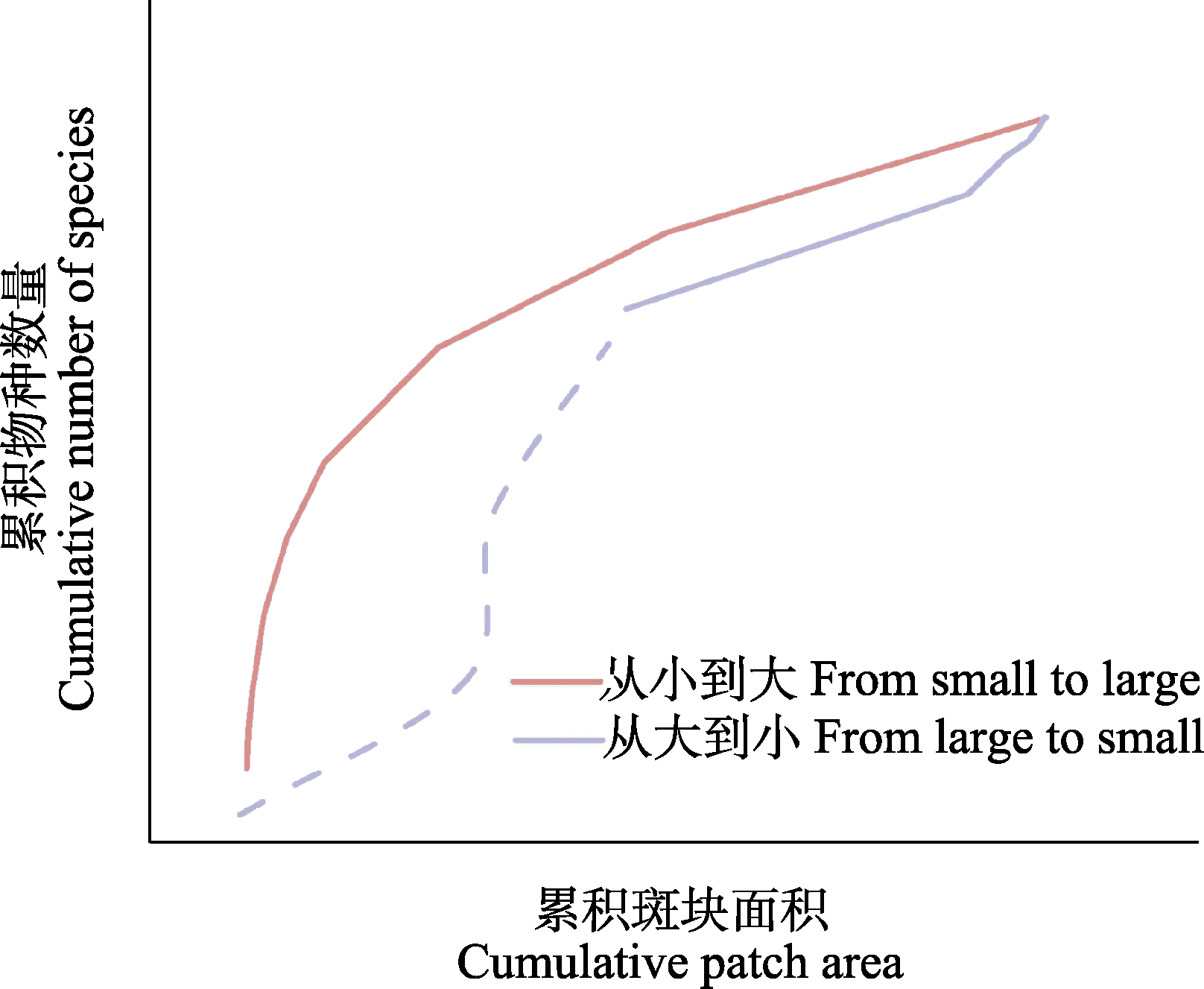
图2
累积种-面积关系曲线示意图。数据点之间的线段按S = cAz进行非线性插值而来, 虚线代表从大到小曲线上的最大斑块面积对应的点与原点的非线性累积趋势。
正文中引用本图/表的段落
Cook (1995)使用两种方式对饱和指数进行了完善。最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962)。然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI。NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995)。由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况。
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ... Quantifying factors for understanding why several small patches host more species than a single large patch 3 2020 ... Theoretical hypotheses and mechanisms for predicting SLOSS patterns (modified from Fahrig et al, 2022). SL, Single large protected area; SL, Several small protected areas.
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
大多数关于SLOSS争论的理论模型往往只考虑如何使生态效益最大化, 常忽略了经济因素在SLOSS争论中的重要性(Groeneveld, 2005), 包括经济成本、财政支出等, 而经济模型则综合考虑了生态效益和经济效益, 从而能够在资源有限的情况下对其进行合理分配以达到预期目标. ... Endangered plants in novel urban ecosystems are filtered by strategy type and dispersal syndrome, not by spatial dependence on natural remnants 1 2020 ... 其次, SLOSS争论还促进了景观层面的保护规划和管理.在人类活动频繁的地区, 连续的大型栖息地通常已经变得非常稀少, 这时多个小斑块的保护对于生物多样性的维持至关重要(R?sch et al, 2015).比如, Planchuelo等(2020)的研究指出, 在城市化地区, 小型自然遗迹可以充当相邻生态系统的种子源且往往包含一些稀有物种, 因此具有较高的保护价值.重视这些地区的保护将有效提高生境特化植物类群的多样性.然而, 除了物种丰富度的总体水平之外, 其他因素也会对生境保护的决策产生影响.例如, 一些生态功能的实现可能需要完整的大型区域(Perino, 2019).此外, 相较于多个小保护区而言, 一个大的保护区更有利于管理(Higgs & Usher, 1980).同时, 当保护目标是针对一个特定的濒危物种时, 保护单一大型的连续区域通常比保护少数小型区域更有效(Fahrig et al, 2022).例如, Woodroffe (2000)指出, 人类活动范围和人口密度的增加与大型食肉动物的灭绝密切相关.因此, 大片连续的自然保护区可以减少这种易被发现的物种与人类相遇的概率从而降低它们被捕猎的风险(Müller et al, 2014). ... The canonical distribution of commonness and rarity 3 1962 ... Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
Cook (1995)使用两种方式对饱和指数进行了完善.最初, 她根据幂函数种-面积关系S = cAz对从小到大曲线和从大到小曲线上的点使用非线性方式进行连接(图2), 其中S为一个地点的物种数, A为面积, c是常数, z是回归指数(Preston, 1962).然后, 将两条曲线的积分之差除以研究区域(如群岛、生境斑块)的总面积和总物种数的乘积, 得到了推导出来的饱和指数NSI.NSI的取值范围为-1到1, 正值代表几个小斑块中容纳的物种数更多, 负值则相反(Cook, 1995).由于最大岛屿与原点之间并不一定呈线性累积趋势(Fahrig, 2020), 因此这种对原始饱和指数进行非线性改进的方式减少了分析结果被高估的情况. ...
本文的其它图/表
-
 表1
与SLOSS争论相关的概念
表1
与SLOSS争论相关的概念
-
 图1
物种累积曲线法(SLOSS比较法)示意图。在给定的栖息地总面积下, (a)从小到大的曲线完全高于从大到小的曲线, 代表SS > SL; (b)从大到小的曲线完全在从小到大曲线的下方, 代表SL > SS; (c)两条曲线交叉(inconclusive), 代表无法确定。
图1
物种累积曲线法(SLOSS比较法)示意图。在给定的栖息地总面积下, (a)从小到大的曲线完全高于从大到小的曲线, 代表SS > SL; (b)从大到小的曲线完全在从小到大曲线的下方, 代表SL > SS; (c)两条曲线交叉(inconclusive), 代表无法确定。
-
 表2
现有饱和指数和SLOSS指数及其特征
表2
现有饱和指数和SLOSS指数及其特征
-
 图3
用于表征从小到大累积曲线(红色)和从大到小累积曲线(灰色)之间偏差的ξ统计量以及指标ΔA示意图。Ψ代表从最大斑块面积推导出的两条曲线下面积的差值; ΔA表示估算两个面积的区域范围。图(a)表示ξ统计量为正的情况, 图(b)代表ξ统计量为负的情况。
图3
用于表征从小到大累积曲线(红色)和从大到小累积曲线(灰色)之间偏差的ξ统计量以及指标ΔA示意图。Ψ代表从最大斑块面积推导出的两条曲线下面积的差值; ΔA表示估算两个面积的区域范围。图(a)表示ξ统计量为正的情况, 图(b)代表ξ统计量为负的情况。
-
 图4
推导ISU和IDI指数的示意图。(a)表示直接将黄色区域面积减去或除以黄色区域和紫色区域面积之和的情况; (b)表示将所有黄色区域的面积相加再对全部的黄色区域和紫色区域面积的总和作减法或除法的情况。
图4
推导ISU和IDI指数的示意图。(a)表示直接将黄色区域面积减去或除以黄色区域和紫色区域面积之和的情况; (b)表示将所有黄色区域的面积相加再对全部的黄色区域和紫色区域面积的总和作减法或除法的情况。
-
 表3
现有理论模型及目标评估
表3
现有理论模型及目标评估
-
 表4
预测SLOSS模式的理论假说和机制(修改自Fahrig等, 2022)。SL: 一个大的保护区; SS: 几个小的保护区。
表4
预测SLOSS模式的理论假说和机制(修改自Fahrig等, 2022)。SL: 一个大的保护区; SS: 几个小的保护区。
-
 图5
当物种呈聚集分布时, 少量大斑块相交的物种数量(a)少于几个小斑块(b)和(c)。不同的颜色及相应的形状代表生境丧失前单个连续栖息地中的不同物种。黑色方框代表因生境丧失而形成的斑块。当少数大斑块和几个小斑块的斑块边缘之间的最大距离相等或类似时, 几个小斑块集能更均匀地覆盖在整个景观中, 因此相交的物种数更多(Fahrig et al, 2022)。(a)中2个大斑块与3个物种相交, 然而(b)中5个小斑块与6个物种相交。在斑块之间相距较远的情况下, 这种效应还会放大: (c)中5个小斑块相交了11个物种(该图改自Fahrig等, 2022)。
图5
当物种呈聚集分布时, 少量大斑块相交的物种数量(a)少于几个小斑块(b)和(c)。不同的颜色及相应的形状代表生境丧失前单个连续栖息地中的不同物种。黑色方框代表因生境丧失而形成的斑块。当少数大斑块和几个小斑块的斑块边缘之间的最大距离相等或类似时, 几个小斑块集能更均匀地覆盖在整个景观中, 因此相交的物种数更多(Fahrig et al, 2022)。(a)中2个大斑块与3个物种相交, 然而(b)中5个小斑块与6个物种相交。在斑块之间相距较远的情况下, 这种效应还会放大: (c)中5个小斑块相交了11个物种(该图改自Fahrig等, 2022)。
|


