SLOSS争论研究进展: 分析方法、理论机制及保护实践
章洋, 王彦平
生物多样性
2025, 33 ( 7):
25081-.
DOI: 10.17520/biods.2025081
生物多样性保护领域中的SLOSS (single large or several small)争论概述了在总面积相等或资源有限的情况下, 应该优先保护一个大的保护区(SL)还是几个小的保护区(SS)来最大化保护物种多样性的问题。自20世纪70年代以来, 该问题一直备受生态学家和保护生物学家的关注, 其研究对于保护区设计以及生物多样性保护具有重要意义。随着研究方法的发展和交叉学科的兴起, SLOSS争论在分析方法和理论机制方面都取得了重要的阶段性进展。本文通过文献检索和归纳总结对SLOSS争论的研究现状进行了综述。首先, 我们回顾了SLOSS争论的起源及其对生物多样性保护的重要性。其次, 本文概括评估了SLOSS争论在实证研究和理论方面的分析方法, 包括零模型法、经典的物种累积曲线法以及由该方法所计算出来的饱和指数。随后, 本文还回顾了以往研究者提出的改进的饱和指数, 并介绍了我们所开发的优化后的饱和指数。此外, 本文探讨了几种影响SLOSS争论的理论机制, 如由灭绝率和定殖率的变化所主导的灭绝-定殖动态理论机制及其相应的检验方法。最后, 本文对该领域进行了总结和展望并为未来的发展方向提出了一些针对性建议, 包括采用多种保护策略的重要性以及在保护区规划中经济和生态因素的结合的必要性。本文整合了SLOSS争论中常用的分析方法的适用场景与局限性, 比较了不同方法在划分保护优先级时的优势和争议点, 可为研究者在方法选择及保护规划权衡方面提供参考。
| 指数划分 Classification of indices | SLOSS相关指数
SLOSS-related indices | 特征 Characteristics
| 参考文献 References | | 原始饱和指数 Original saturation index | OSI | 计算结果容易倾向于几个小斑块, 未考虑物种占用对斑块大小的依赖性。OSI tends to skew the calculations in favor of several small patches. It does not take into account the dependence of species occupancies on patch size. | Quinn & Harrison, 1988; Deane, 2022; | | 改进的饱和指数 Improved saturation index | NSI | 减少了高估分析结果的情况。Improved saturation indices avoid the overestimation of analytical results. | Cook, 1995 | | 优化的饱和指数 Optimized saturation index | ISU、IDI | 在Mac Nally和Lake (1999)的基础上提出的新指数, 可用于计算累积物种、功能和谱系3个维度的多样性, 并能避免对计算结果的高估或低估。
New indices based on Mac Nally and Lake (1999), which can be used to calculate the diversity of cumulative species, functional and phylogenetic dimensions and can avoid overestimation or underestimation of the results. | 本文提出 This study
| | 修正的Quinn-Harrison统计量 Modified statistics of Quinn-Harrison method | ξ、η | ξ可以衡量从小到大和从大到小方向上累积多样性的差异; η能够更直观地判断SL还是SS在系统中占主导地位。ξ measures the difference in cumulative diversity in the small to large and large to small directions. η enables a more intuitive determination of whether SL or SS dominates the system. | Mac Nally & Lake, 1999 | | 外推的SLOSS指数 Extrapolated SLOSS index | SLEX | SLEX减少了抽样偏差带来的影响; 还能反映生境破碎化对物种丰富度的影响。SLEX reduces the impact of sampling bias. It can also reflect the impact of habitat fragmentation on species richness. | Boecklen,1997; Gavish et al, 2012 |
View table in article
表2
现有饱和指数和SLOSS指数及其特征
正文中引用本图/表的段落
在许多SLOSS实证研究中, 单位面积采样点的数量会随着斑块面积的增大而下降(采样强度减小), 从而使SLOSS的研究结果偏向于SS (Gavish et al, 2012)。也就是说将斑块组合成面积相等的集合时, 包含很多小斑块的子集比包含少数大斑块的子集拥有更多的采样点, 促使几个小斑块中发现给定物种的概率更高(Fahrig, 2020)。这导致不少研究者认为测试SLOSS的饱和指数是有偏差的。因此, 随着相关研究的深入, 一些改进的饱和指数被相继提出, 这些指数均对Quinn和Harrison (1988)的原始饱和指数进行了优化(表2)。因此, 本文对以往研究者所提出的优化后的指数以及我们开发的改进后的饱和指数进行讨论和分析, 并说明这些指数相较于原始指数的优势所在。
Gavish等(2012)认为Boecklen (1997)的方法没有控制采样强度的影响, 因而他们对SLOSS指数进行了改善, 包括运用软件包ws2m (Turner et al, 2003)和F5 (Rosenzweig et al, 2003)估计式来计算物种多样性以减少偏差。具体来说, Gavish等(2012)使用了幂函数模型的种-面积关系而不是半对数种-面积关系, 因为前者对数据的拟合效果更好。该步骤是通过对观测到的物种数和斑块面积利用对数-对数最小二乘线性回归来实现的。其次, 将所有斑块的总面积代入回归方程, 得到一个与总生境斑块面积相等的理想斑块的期望物种数Ssl (单一大型保护区策略)。接着, 将所有斑块的实测物种数Sss (几个小型保护区策略)减去Ssl然后除以Sss来计算SLOSS指数, 即改善后的外推的SLOSS指数 = 100% × (Sss - Ssl)/Sss。在本文中, 我们将其表示为SLEX (表2)。根据定义可知, SLOSS指数表示的是几个小斑块相较于一个大斑块物种丰富度的变化(Gavish et al, 2012)。例如, 当SLOSS指数为30%时, 表明所研究系统的几个小斑块比单个连续生境斑块包含的物种数多30%。另外, SLEX指数还能反映生境破碎化效应对物种丰富度的影响, 即当SLEX大于、小于和等于零时, 分别表示正的、负的和中性的破碎化效应(Liu et al, 2022)。
大多数关于SLOSS争论的理论模型往往只考虑如何使生态效益最大化, 常忽略了经济因素在SLOSS争论中的重要性(Groeneveld, 2005), 包括经济成本、财政支出等, 而经济模型则综合考虑了生态效益和经济效益, 从而能够在资源有限的情况下对其进行合理分配以达到预期目标. ... SLOSS-based inferences in a fragmented landscape depend on fragment area and species-area slope 1 2022 ... Gavish等(2012)认为Boecklen (1997)的方法没有控制采样强度的影响, 因而他们对SLOSS指数进行了改善, 包括运用软件包ws2m (Turner et al, 2003)和F5 (Rosenzweig et al, 2003)估计式来计算物种多样性以减少偏差.具体来说, Gavish等(2012)使用了幂函数模型的种-面积关系而不是半对数种-面积关系, 因为前者对数据的拟合效果更好.该步骤是通过对观测到的物种数和斑块面积利用对数-对数最小二乘线性回归来实现的.其次, 将所有斑块的总面积代入回归方程, 得到一个与总生境斑块面积相等的理想斑块的期望物种数Ssl (单一大型保护区策略).接着, 将所有斑块的实测物种数Sss (几个小型保护区策略)减去Ssl然后除以Sss来计算SLOSS指数, 即改善后的外推的SLOSS指数 = 100% × (Sss - Ssl)/Sss.在本文中, 我们将其表示为SLEX (表2).根据定义可知, SLOSS指数表示的是几个小斑块相较于一个大斑块物种丰富度的变化(Gavish et al, 2012).例如, 当SLOSS指数为30%时, 表明所研究系统的几个小斑块比单个连续生境斑块包含的物种数多30%.另外, SLEX指数还能反映生境破碎化效应对物种丰富度的影响, 即当SLEX大于、小于和等于零时, 分别表示正的、负的和中性的破碎化效应(Liu et al, 2022). ... On the generation of diversity in archipelagos: A re-evaluation of the Quinn-Harrison ‘saturation index’ 13 1999 ... 物种累积曲线法的优势在于操作简单、结果直观, 因此自提出以来在SLOSS争论中得到了广泛应用.然而, 物种累积曲线法也存在一定的局限性, 其分析结果往往倾向于“SS > SL” (Gavish et al, 2012; Deane, 2022).例如, Mac Nally和Lake (1999)通过模拟分析表明, 即使真实情况是“SL > SS”, 物种累积曲线的排序方法仍可能错误地显示为“SS > SL”.这是因为小斑块集的生境异质性更高, 导致SS曲线早期累积速率更快, 但未必代表真实的总物种数.此外, 由于种-面积关系和被动采样效应之间存在密切联系, 当物种以从小到大的顺序累积时, 由于较大的斑块理论上应该包含更多的物种, 因此从小到大顺序累积的每一步添加的较大斑块本身具有更高的物种数, 从而增加了新物种发现的概率, 这说明从小到大曲线的物种累积速度更快(Deane, 2022), 从而导致“SS > SL”模式频繁出现.Mac Nally和Lake (1999)指出Quinn和Harrison (1988)的方法并不可靠, 因此他们对饱和指数进行了改进后提出了一种新的统计方法并将其应用于3个示例数据集, 得出SS在大多数研究中占主导地位的情况是一种假象, 并且在使用Quinn和Harrison (1988)的简单图形法时, SL的优势在一定程度上被掩盖了. ...
本文的其它图/表
-
表1
与SLOSS争论相关的概念
-
图1
物种累积曲线法(SLOSS比较法)示意图。在给定的栖息地总面积下, (a)从小到大的曲线完全高于从大到小的曲线, 代表SS > SL; (b)从大到小的曲线完全在从小到大曲线的下方, 代表SL > SS; (c)两条曲线交叉(inconclusive), 代表无法确定。
-
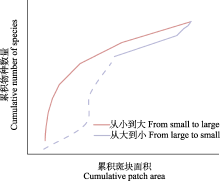图2
累积种-面积关系曲线示意图。数据点之间的线段按S = cAz进行非线性插值而来, 虚线代表从大到小曲线上的最大斑块面积对应的点与原点的非线性累积趋势。
-
图3
用于表征从小到大累积曲线(红色)和从大到小累积曲线(灰色)之间偏差的ξ统计量以及指标ΔA示意图。Ψ代表从最大斑块面积推导出的两条曲线下面积的差值; ΔA表示估算两个面积的区域范围。图(a)表示ξ统计量为正的情况, 图(b)代表ξ统计量为负的情况。
-
图4
推导ISU和IDI指数的示意图。(a)表示直接将黄色区域面积减去或除以黄色区域和紫色区域面积之和的情况; (b)表示将所有黄色区域的面积相加再对全部的黄色区域和紫色区域面积的总和作减法或除法的情况。
-
表3
现有理论模型及目标评估
-
表4
预测SLOSS模式的理论假说和机制(修改自Fahrig等, 2022)。SL: 一个大的保护区; SS: 几个小的保护区。
-
图5
当物种呈聚集分布时, 少量大斑块相交的物种数量(a)少于几个小斑块(b)和(c)。不同的颜色及相应的形状代表生境丧失前单个连续栖息地中的不同物种。黑色方框代表因生境丧失而形成的斑块。当少数大斑块和几个小斑块的斑块边缘之间的最大距离相等或类似时, 几个小斑块集能更均匀地覆盖在整个景观中, 因此相交的物种数更多(Fahrig et al, 2022)。(a)中2个大斑块与3个物种相交, 然而(b)中5个小斑块与6个物种相交。在斑块之间相距较远的情况下, 这种效应还会放大: (c)中5个小斑块相交了11个物种(该图改自Fahrig等, 2022)。
|
