分子钟定年方法(molecular dating approach)是近年来宏观生物学尤其是生物多样性及其格局形成历史相关研究最为重要的手段之一。该方法的基础假设——分子钟假设最早可以追溯至20世纪中叶。1962年, Pauling和Zuckerkandl提出分子钟假设(molecular clock hypothesis; Pauling & Zuckerkandl, 1962), 随后Margoliash等(1963)对其进行了正式的描述: “从两个物种最初分化开始, 它们的细胞色素C残基(residue)序列之间的差异, 是由二者分化后经历时间的长短决定的”。分子钟模型的核心原理是: 在一定时间范围内, 特定生物大分子的序列在不同类群间的差异与其分化后经历的时间呈近似正线性关系。分子钟为进化生物学者提供了将微观证据和宏观进化历史结合起来的、全新的重要方法论。此前, 地球生命的进化历史重建主要结合化石记录和地质历史进行, 但是由于化石埋藏形成的偶然性等因素, 化石记录在不同类群中的稀缺程度大不相同。事实上, 多数生物类群的化石记录, 尤其是大化石记录(macrofossil)十分稀缺(Greenwood, 1991), 导致基于化石记录的进化历史研究较难开展。以分子钟定年方法为代表的整合进化历史重建方法, 可以同时考虑分子证据、形态证据、时间信息等, 通过与分子系统发育与进化等相关的算法和模型, 整合现生生物和古生物的进化历史数据 (Donoghue & Moore, 2003), 形成一棵同时包含现生生物和古生物类群的生命之树(tree of life), 从而打破现生生物研究和古生物研究之间的藩篱, 更加全面地揭示地球生物多样性形成的时间框架。
自1965年分子钟定年方法提出伊始, 许多学者对这一方法提出质疑, 他们认为大分子序列的变化是随机且无规律的(Morgan, 1998)。近二十多年来, 随着DNA测序技术的进步和各类模型算法的不断完善, 分子钟定年方法不断进步, 在各个领域的应用中认可度不断提高(Kumar, 2005; dos Reis et al, 2016)。如今分子钟已经被广泛用于生物学研究的各个领域, 从体细胞突变、癌症细胞进化等微观研究到生物多样性形成历史等宏观研究, 其提供的进化时间框架不可或缺(Kumar & Hedges, 2016; Graham & Sottoriva, 2017)。因此, 如何提高分子钟的可靠性一直是进化生物学和生物地理学等研究领域的重要议题。
利用分子钟模型进行系统发育树构建的方法众多, 如贝叶斯法(Bayesian)、最大似然法(maximum likelihood, ML)、最大简约法(maximum parsimony, MP)、邻接法(neighbor-joining, NJ)等, 而在时间树构建方面以贝叶斯法和最大似然法更为可靠、主流、且衍生方法多样(Hall, 2005; Brooks et al, 2007; Yang & Rannala, 2012)。由于贝叶斯方法在20世纪末才被引入分子系统学领域, 国内介绍贝叶斯框架下分子钟定年方法基本理论框架并提供使用建议的文献仍存在一些空白。21世纪初, 有部分国内学者较早地报道了贝叶斯方法在时间树构建与物种分化时间估计中的应用(张原和陈之瑞, 2003), 后逐渐有学者对贝叶斯框架下分子钟假说及其应用展开报道与论述(鲁丽敏等, 2014; 李可群, 2015; 刘晓枫和张爱兵, 2016; 朱天琪, 2019), 并提供了各类贝叶斯软件的使用流程(鲁丽敏等, 2014; Zhang, 2019), 但对于复杂模型的参数及先验设置的选择讨论较少, 且仍然缺少对于目前最常使用的贝叶斯节点标记法(Bayesian node-dating method)程序的详细介绍。
本文以贝叶斯节点标记法为例, 详细阐述了分子钟定年方法的原理、误差来源, 以及如何规避这些误差, 重点分析了多种情况下节点标记对分化时间估计的影响, 并提供了合理的模型和软件使用建议。
1 贝叶斯节点标记法的基本原理和主要类型
贝叶斯算法自20世纪末被引入分子系统发育与进化领域以来, 随着计算效率的提升和马尔可夫链蒙特卡罗方法的引入(Markov chain Monte Carlo, MCMC; Yang & Rannala, 1997; Chen & Shao, 1999), 它在该领域的应用逐年递增, 目前已经成为分子系统发育与进化领域中可信度和准确度最高的方法之一(Yang & Rannala, 2012; Brower, 2018)。贝叶斯算法整合各项不确定性因素, 随着数据量的增加, 参数收敛到真值。对于每一个参数的概率分布, 观测者都具有一定的经验认知, 即先验分布(prior distribution), 体现了观测者经验的总结和主观预测的结果。通过整合先验分布、给定数据集(data set)以及其他参数, 可以得到各参数的后验分布(posterior distribution)及均值, 体现了主观经验与客观数据的结合。在数据量不足的情况下, 后验由先验主导; 而当数据量逐渐累积, 先验产生的影响逐渐减小, 后验将由客观数据主导(Wasserman, 2004)。然而, 由于生物学数据的局限性, 即便使用全基因组数据也往往难以使后验分布收敛到单一真值, 因此先验分布的设置变得至关重要, 尤其是在数据量较小的分析中(Yang & Rannala, 2006)。
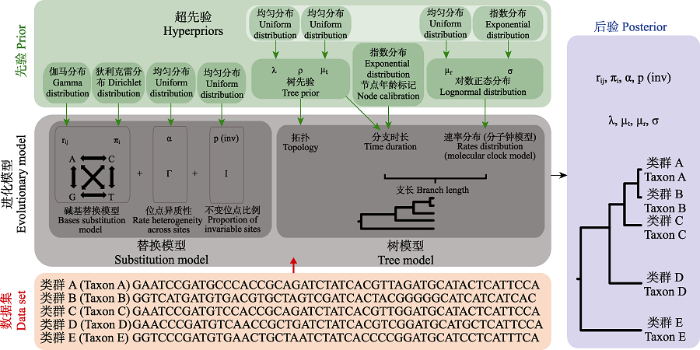
在分子钟模型下使用贝叶斯法进行计算时, 需要设置序列数据(sequence data)、进化模型(evolutionary model)和模型先验(prior; Bromham et al, 2018)。进化模型由核酸(蛋白质)替换模型(substitution model)和树模型(tree model)组成, 两类模型又分别需要进行众多先验值及其分布的设定。替换模型涉及的参数有碱基间替换速率(rate of transition between bases)、碱基频率(base frequencies)、不同位点间替换速率(rate across sites)的分布模型参数以及不变位点(invariant sites)的比例。树模型由树的拓扑(topology)和支长(branch lengths)两部分组成, 支长又由分支时长(branch durations)和分支进化速率(branch rates)共同决定。其中, 不同的参数可以施加不同的先验分布, 而对于其中的一些先验分布的参数还可以进一步设置超先验(hyperprior; Friston et al, 2013), 所有这些设置构成了一个进化模型, 如图1所示。最终, 通过将数据集应用于进化模型, 进行MCMC的抽样和统计分析, 得出时间树和各类参数的后验分布及可信区间(credible intervals)。
图1
图1
贝叶斯法时间树构建过程示意图(改自: Bromham et al, 2018)。进化模型的参数设置是贝叶斯法系统发育树构建的关键步骤, 由替换模型和树模型组成。替换模型包括了碱基替换模型(包括碱基转换速率rij和碱基频率πi参数)、速率的位点(sites)异质型(如Γ分布)以及不变位点的比例p(inv)。树模型可以解构为结构与支长两个组份。结构由树先验决定, 图中使用的是生灭过程模型, 包含物种生成率(λ)、物种灭绝率(μt)和取样频率(ρ)三个参数。在“两步法”中, 结构还可以来自于树文件的输入。支长由分支时长与速率分布共同决定。分支时长一方面受树先验的影响, 另一方面与节点年龄标记密切相关; 速率分布即分子钟模型, 决定了进化速率在不同支上的分布格局。数据集与进化模型共同计算得到各参数的后验及时间树。
Fig. 1
Schematic diagram of Bayesian time tree construction (modified from: Bromham et al, 2018). The parameter setting of evolutionary models is the key step of constructing phylogenetic tree based on Bayesian method, which is composed of substitution model and tree model. The substitution model includes base substitution model (including base conversion rate rij and base frequency πi as parameters), site heterogeneity of rate (such as Γ distribution) and proportion of invariant sites p(inv). The tree model can be decomposed into two components: structure and branch lengths. The structure is determined by tree priors (in this case the birth and death process model), which includes three parameters: species generation rate (λ), species extinction rate (μt) and sampling frequency (ρ). In the “two-step” method, the structure can also come from the input of the tree file. The branch length is determined by the branch duration and the rate distribution across branches. The branch duration is influenced by tree priors and node age calibration. The rate distribution is recognized as clock models, which determine the distribution pattern of evolution rate on different branches. The data set is applied to the evolutionary model to generate posteriors of each parameter and the time tree.
在使用分子数据进行系统发育树的构建时, 尽管分子序列数据的增加能够提高系统发育树的准确度和精确度(dos Reis et al, 2012; Warnock et al, 2017), 但由于核酸(蛋白质)替换速率在不同进化分支(evolutionary lineages)间的差异、不同地质时期古环境因素导致进化速率的不同(Harwood et al, 2007; Laws, 2010)、世代时间各异(Thomas et al, 2010)等因素, 只能得到系统发育树的拓扑以及相对物种分化时间, 而无法得到谱系间的绝对物种分化时间, 即只知道树的拓扑和相对支长(遗传距离)而不知绝对支长。分支时长由树先验(tree prior)和校准信息(calibration, 包括节点标记(node calibration)和端点标记(tip calibration))共同决定, 在没有化石证据等提供校准信息时, 仅依靠树先验得到相对年龄参考价值较低。因此, 在贝叶斯框架下得到相对分化时间后, 要进一步得到绝对分化时间, 最好的方法是进行化石标定(fossil calibration; Barba-Montoya et al, 2017)。在获得某个类群的化石及其年龄后, 就可以在相对分化时间框架的基础上整合化石年龄, 得出进化时间树, 从而得出该类群进化树上各个节点的绝对分化时间及其可信区间。
在贝叶斯框架下常用的化石标记方法包括节点标记法(node-dating)、全证据法(total-evidence method; Ronquist et al, 2012)以及化石生灭进程法(fossilized birth-death process; Heath et al, 2014)等。节点标记法使用化石年龄数据标定系统发育树上的相应节点; 全证据法和化石生灭进程法属于端点标记法(tip-dating), 将化石视作系统发育树上的进化分支进行树的构建, 充分利用了化石类群的形态特征, 而不仅限于整合其年龄数据。三类方法各有利弊(Grimm et al, 2015): 节点标记法虽然考虑了树的结构和化石标记的不确定性(uncertainty), 但对化石年龄先验(作为时间先验)的设置往往武断(Sauquet, 2013), 只考虑使用年龄最老的化石, 且得到的系统发育树中只包含现存类群; 全证据法基于系统发育关系进行化石定位, 同时考虑了化石类群和现存类群的定年, 但需要依赖化石及现存类群的形态矩阵(morphological matrix), 这一条件有时难以满足, 且往往需要花费大量时间对现存物种的形态学数据进行编码(Guillerme & Cooper, 2016); 化石生灭进程法能够运用所有的化石类群, 并且不需要形态学矩阵, 但没有考虑到系统发育树的结构和化石年龄的不确定性。根据其不同的特性, 以上三种方法分别适用于化石记录贫乏的类群、形态性状丰富的类群, 以及化石记录丰富的类群(Grimm et al, 2015)。尽管在某些情况下, 节点标记法并不是最好的方法(Ronquist et al, 2012), 但由于目前多数类群的化石记录较为匮乏、形态学特征编码困难等问题,节点标记法仍然是目前适用范围最广、最常用的化石标记方法。此外, 由于目前整合了形态学数据的系统发育研究得出的关键节点年龄有时过于古老, 令研究人员难以接受, 其算法的可靠性有待验证和进一步改进(dos Reis et al, 2015)。因此, 在下文中我们主要讨论影响节点标记法准确度(accuracy)与精确度(precision)的因素以及如何提高物种分化时间分子定年的可靠性。
2 贝叶斯节点标记方法的主要误差来源
主流贝叶斯节点标记方法的主要误差来源有3个方面: (1)替换速率模型(substitution rates models)和系统发育树结构(tree topology)引入的误差; (2)分子钟模型(molecular clock models)引入的误差; (3)节点年龄标记方式(calibrations)引入的误差。
2.1 替换速率模型和系统发育树结构引入的误差
不同类群生物的核酸、蛋白质替换速率不同(类群世代长度、DNA修复机制不同等), 同一物种的不同位点的替换速率也不同, 这要求研究者在设置分子钟模型时需要同时考虑多个维度的位点替换概率分布。通常来说, 在比较物种之间的基因编码区核酸序列差异时, 第一位、第二位密码子的突变率与时间具有良好的共线性, 而第三位密码子的突变率远高于第一、第二密码子, 且与时间之间呈现非线性关系。Strugnell等(2005)研究发现, 第三密码子明显存在饱和信号, 表明其结果并不可靠。因此在研究进化速率变异较大的类群以及类群跨度较大的系统发育树时, 可以考虑排除第三密码子。同理, 当一个基因位点或密码子位点的替换速率与其他位点有显著差异、数值异常, 且对后验概率的整合产生严重影响时, 可以考虑去除该位点(Ronquist et al, 2012), 也可以对各部分数据采取不同的分组(partitions)替换速率模型。诸如PartitionFinder (Lanfear et al, 2012)等软件能够对不同基因、不同密码子位点的组合进行比较, 每个组合使用不同的替换速率模型, 从而寻找最合适的分组模型, 其结果可以直接应用于BEAST、MrBayes等主流贝叶斯分析软件。
另外, DNA序列中同一位点的4种碱基之间的替换速率并不相同, 因此出现了许多不同的替换模型。目前最常用的替换模型是general time- reversible模型家族, 包括JC69模型(Jukes & Cantor, 1969)、HKY85模型(Hasegawa et al, 1985)、K80模型(Kimura, 1980)、F81模型(Felsenstein, 1981)和GTR模型(Tavaré, 1986)等, 其中GTR模型最为复杂, 它允许每一种核酸替换都有不同的替换速率。该家族其余模型的区别在于不同核酸间的替换速率有多少是相同的(例如JC模型假设所有替换速率都是相同的; Jukes & Cantor, 1969)。位点间异质性(site heterogeneity)可以体现为伽马分布(Gamma distribution, Γ, 假设位点间替换速率符合伽马分布)、恒定速率(invariable, I, 假设位点间替换速率独立且恒定)以及I + Γ模型等。不同的模型组合可以被描述为诸如JC69+Γ、HKY85+Γ和GTR+Γ+I等模式。目前多个软件能够根据数据集对替换模型的适合度进行检验, 例如JModelTest (Darriba et al, 2012)、Modelgenerator (Keane et al, 2006)、bModelTest (Bouckaert & Drummond, 2017)等, 从而得出特定数据集最优的碱基替换模型或者数据集不同部分碱基替换模型的最优组合。Shapiro等(2006)使用酵母和病毒的序列对不同等替换模型、位点异质性模型和密码子位点模型等组合进行了检验, 结果显示, 考虑了密码子位点异质性的模型往往是最好的, 而HKY、GTR、I和Γ模型组合的适合度各有差异, 模型组合在不同类群中的适合度也不同。
在开展分子钟应用时, 系统发育树相对支长和结构是最基础的信息, 一般需要利用现存物种的生物大分子序列信息来构建系统发育树。然而, 在主流的系统发育树构建方法中, 相较于距离法(distance methods)、简约法(parsimony methods)和似然法(likelihood methods), 贝叶斯法能够利用复杂模型最大程度地考虑系统发育树构建中存在支长和结构的不确定性, 具有较好的准确度和可靠性(Beerli, 2006; Yang & Rannala, 2012)。
利用贝叶斯软件构建时间树时, 树的拓扑可以来自导入的物种树文件, 也可以来源于集成性贝叶斯软件(如BEAST; Drummond et al, 2012)的计算结果, 后者主要包括两类: 一类基于溯祖理论(coalescent theory), 另一类基于物种形成理论(speciation theory)。目前常用的树先验设置主要基于物种形成理论, 包括生灭模型(birth-death model)和尤尔模型(Yule model)等。在设置树先验时, 由于不用树先验的假设不同, 可能会引入误差。例如生灭模型和尤尔模型在苏铁类进化时间框架构建过程中, 二者得出的分化时间差异明显, 后者得出的节点年龄普遍更大(Condamine et al, 2015)。
拓扑误差最典型的例子是长支吸引(long branch attraction, LBA)。长支吸引是系统发育树构建中常遇到的问题之一(Susko, 2015), 在2000年前后其陆续被发现存在于真核生物众多类群的系统发育分析研究中(Reyes et al, 2000; Brinkmann et al, 2005)。如果一棵树的真实情况是有两个外部长支被一个内部短支连接并隔开, 那么最后结果可能会得到两个长支聚在一起的错误的树结构。这一现象可能在利用简约法以及模型过于简单且未考虑位点替换速率异质性的最大似然法和贝叶斯法建树的过程中出现(Yang & Rannala, 2012)。产生这一现象的原因是, 序列中某些位点产生了多次的替换, 因此分析的位点越多, 长支吸引现象就越有可能发生。长支吸引的解决方案之一是, 尽量使用全似然法(full likelihood method, 包含最大似然法和贝叶斯法), 使用合理位点替换模型, 并剔除进化速率过快的位点, 同时比较多次运算产生的系统发育树, 进行交叉检验(Susko, 2015)。因为树的拓扑关乎物种之间的共祖关系和化石标记点放置等, 所以在进行节点标记前应确保拓扑的准确性。
2.2 分子钟模型引入的误差
不同分子钟模型处理不同分支间进化速率差异的方式不同, 可能影响时间树上的节点年龄。
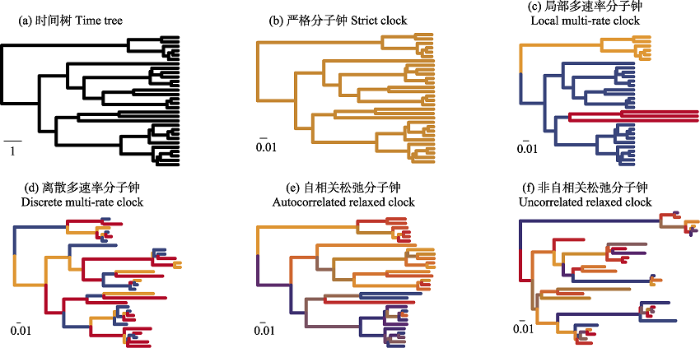
简单的分子钟模型得出的时间树上, 姊妹分支之间的绝对支长是相等的, 但是它们的相对支长存在差异, 二者之间的进化速率也存在差异, 因此需要进行相应的优化。依照速率优化方式的不同, 主流的分子钟模型可以分为严格分子钟(strict clock)、多速率分子钟(multi-rate clock)和松弛分子钟(relaxed clock; Ho & Duchêne, 2014)。近年来由于核酸和氨基酸替换速率在不同位点、不同类群间的差异问题受到越来越多的关注, 某些特定的松弛分子钟模型如非自相关对数正态分布松弛分子钟模型(uncorrelated lognormal relaxed clock, ULRC), 越来越受到欢迎(Miller & Bergsten, 2012)。
严格分子钟模型(图2b)规定系统发育树中所有谱系的替换速率为一个恒定的单一的值, 主要应用于近缘物种, 如同属或序列差异小于5%的物种(Yang, 2006)和种下单元之间的系统发育构建, 因为各分支之间的替换速率变化往往很小(Brown & Yang, 2011; Ho & Duchêne, 2014), 这种情况下严格分子钟相较松弛分子钟具有更为显著的优势(Brown & Yang, 2011)。但对于替换速率变化较大的类群, 严格分子钟模型的准确度则很低(Wertheim et al, 2010)。多速率分子钟模型允许多于一种、但少于总物种数的速率设定存在于系统发育树中, 这意味着部分谱系将共享位点替换速率。在一些多速率分子钟模型中, 聚在一起的类群具有相同或相似的替换速率, 称为局部分子钟(local multi-rate clock; 图2c); 在另一些多速率模型中, 速率的变化则贯穿整棵树, 称为离散多速率分子钟(discrete multi-rate clock; 图2d; Ho & Duchêne, 2014)。
图2
图2
不同的分子钟模型示意图(改自: Ho & Duchêne, 2014)。图中的6个时间树具有相同的结构, 但由于分子钟模型选择的不同, 支长有很大差异。(a)未添加分子钟模型的时间树, 比例尺显示了1个时间单位。(b)严格分子钟模型, 所有支的速率相等。(c)局部多速率分子钟, 允许一定量的速率存在, 并根据拓扑的聚类情况设置速率, 同一类群具有相同或相似的速率。(d)离散多速率分子钟, 允许一定量的速率存在, 不考虑拓扑聚类情况的模型。(e)自相关松弛分子钟, 允许最多等于支数的速率存在, 且邻近支的速率相关。(f)非自相关松弛分子钟, 没有任何对速率的数量、分布格局的限制, 是最宽松自由的模型设置。
Fig. 2
Schematic diagram of different molecular clock models (modified from Ho & Duchêne, 2014). The six time trees in this figure have the same structure, but the branch length varies greatly due to different selection of molecular clock models. (a) The time tree without applying molecular clock model. The scale bar indicates one time unit. (b) In strict molecular clock model, all branches have the same rate. (c) Local multi-rate molecular clock allows a certain amount of rate and sets the rate according to the clustering situation of topology. The related branches have the same or similar rate. (d) Discrete multi-rate molecular clock, which also allows a certain amount of rate, does not consider the topological clustering. (e) The autocorrelated relaxed molecular clock allows the existence of a rate at most equal to the number of branches, and the rate dependence of adjacent branches. (f) The uncorrelated relaxed molecular clock, without any restrictions on the number and distribution pattern of rates, is the most relaxed and free model setting.
松弛分子钟模型允许每一个谱系具有独特的替换速率, 考虑了每一个谱系的独立性。该模型要求给出先验以便对支长进行模拟(branching process prior), 这一过程中常用的有生灭进程模型(同时考虑物种的生成和灭绝)和尤尔模型(生灭进程模型的特殊情况, 仅考虑物种生成率)等。在很多情况下生灭进程模型比尤尔模型更符合实际情况, 尤其是在物种灭绝率较高的类群中(Condamine et al, 2015), 并且使用后者得到的节点年龄极有可能比前者大(Wang & Mao, 2016)。在贝叶斯框架下, 常见的松弛分子钟模型又可以分为自相关松弛分子钟(autocorrelated relaxed clock, 图2e; Thorne et al, 1998)和非自相关松弛分子钟(uncorrelated relaxed clock, 又称独立速率分子钟; 图2f; Drummond et al, 2006)两种: 自相关模型中, 相邻谱系之间的替换速率是相关联的, 体现了谱系之间的生物学特性; 而非自相关模型中, 任何分支之间的替换速率都是独立的, 能够避免某些快速进化事件对分化年龄估算带来的影响。自相关松弛分子钟有多种速率分布可以选择, 常见的有对数正态分布、伽马分布等, 每个分支上的速率都来自于速率分布, 速率的变化和时间成正比, 因此自相关松弛分子钟能够体现数量性状的进化过程。它的缺陷之一在于其对替换速率的变化范围没有限制, 即替换速率可能随时间不断提高。为了消除这一不稳定状态, 可以使用内置于RevBayes (Höhna et al, 2016)等软件中的更加复杂的Ornstein-Uhlenbeck模型(Cooper et al, 2016; Halliday & Goswami, 2016)和Cox-Ingersoll-Ross模型(Lepage et al, 2006; Ho & Duchêne, 2014)等。非自相关分子钟每个分支上的速率都来源于速率先验分布。与自相关分子钟模型不同的是, 其分支之间的速率相对独立, 相互之间没有关联。非自相关分子钟模型更适用于研究快速进化事件对物种分化的影响, 并考虑到了系统发育关系与化石标记的不确定性(Smith et al, 2010)。自相关模型和非自相关模型各有优缺点, 在条件允许的情况下可分别使用两种模型构建系统发育树, 并比较其差异, 选择较优模型。
需要注意的是, 上述各类模型没有优劣之分, 只是各自适用的情况不同(Lee, 2016), 需要通过实践, 利用客观参数(如贝叶斯因子)进行比较后慎重选择。除了上述的替代模型和速率先验外, 节点年龄标记方式也会对系统发育树的构建产生巨大影响, 节点年龄标记方式设置不合理将直接导致物种分化时间估算产生误差。
2.3 节点年龄标记方式引入的误差
节点年龄标记是节点标记法时间树构建的必要步骤, 绝对时间信息的来源主要包含: (1)化石标记(fossil calibration); (2)二次标记(secondary calibration); (3)使用生物地理学事件年龄进行标定(biogeographic/vicariance calibration)等。
2.3.1 化石标记
(1)标记化石选择。分子数据(氨基酸、DNA序列)只能提供相对的进化时间框架, 而绝对分化时间的最终来源是从相关化石中提取的年龄信息(Warnock et al, 2017)。分子数据量的增加能够提供更多信息, 从而提高系统发育拓扑和相对分化时间框架的可靠性, 但物种分化时间估算的准确度和精密度主要由化石标记的质量决定, 因此化石标记是物种分化时间估算中最为重要的环节之一(Parham et al, 2012)。
由于化石记录是一个不断挖掘、动态更新的集合, 因此研究者在使用化石标记时必须格外小心地筛选和采用可靠的化石记录。随着古生物学的发展, 不断有新的化石被发掘出并被标定年龄, 我们无法知道某一个化石是否为该类群在地球上存在的最古老的化石, 而只知道该类群分化产生的时间至少早于该类群目前已知的、最古老化石的年龄。因此, 使用贝叶斯化石节点标记的主流策略之一, 是使用目前已知最古老的化石作为一个或多个冠部节点(crown node)的年龄下限(minimum age constraint), 并往往使用至少一个公认、相对确定的年龄作为根节点(root node)或接近根部的节点的年龄上限(maximum age constraint), 两者同时作为时间边界, 从而使系统发育树的节点年龄结构逐渐趋于稳定(Marshall, 2008)。如果没有最大年龄限制, 那么所得的时间树中, 多数节点的年龄都有高估的潜在可能性(Claramunt & Cracraft, 2015)。
虽然实践中通常选择一个类群中已知最古老的化石, 但在选择分子钟标记化石时, 化石本身的特性也是需要权衡的重要因素。对于化石的选择主要考虑两个指标: (i)其年龄是否能够代表一个类群的最大年龄(代表性, representative); (ii)其分类学特征是否符合系统发育分析的需求(分类学可分析性, taxonomic solution; Sauquet et al, 2012)。具有代表性的化石需要能够在该类群刚刚分化出来时就能够形成、留存到现在并得以被挖掘和发表; 化石的可分析性则需要化石既拥有足够的、便于聚类的共有衍征(synapomorphies), 除此之外, 又需要足够的与其他类群的差异性特征, 才能将化石可靠地放置在系统发育树中相应的标记节点上。化石的可分析性由其完整度、可比对数据集的采样频率等共同决定(Fikáček et al, 2020)。Fikáček等(2020)依据系统发育辨析度将化石分为3类: (a)依据形态特征能明显将其放在进化树上的某一位置, 且无其他备选项; (b)在进化树上有几个接近的备选位置, 支持度相近并存在一定冲突(例如由于趋同演化, convergent evolution); (c)在进化树上有众多的备选位置, 后验概率都很低, 表明化石的形态特征信息缺失较多、其系统发育位置辨析度低。(a)和(b)类化石是节点年龄标记的较优选择, 在使用系统发育的方法进行辨析后即可确定位置, 而(c)类化石难以提供有效且准确的信息。
能够同时满足代表性和可分析性两个特征的化石是最理想的, 但遗憾的是大多数的化石只能满足其中一项, 这两类化石分别被描述为“古老但有风险(old but risky)”和“年轻但可靠(young but safe)”。“古老但有风险”的化石的年龄能够代表该类群已知的最大年龄, 即该类群刚刚分化产生便有化石并能够较为完整地留存到现在, 然而其分类学特征往往难以满足系统发育分析的需要(如花粉化石), 这类化石常由于其形态的模糊性(如上文中的c类化石)而只能使用直觉法(一种较为主观的方法, 见下文)确定标记节点, 适合用于标定类群早期分化的节点(如根节点); “年轻但可靠”的化石往往无法准确体现(通常会低估)该类群分化产生的时间, 但是其性状具有很强的可分析性(如上文中的a类化石), 使用上较为安全(并不等于准确), 能够进行更加复杂的系统发育分析, 例如多数叶、花、果实的化石(Sauquet et al, 2012)。此外, 对于(b)类化石, 应该将其放置在不同位置上进行标记, 并将得出的结果进行比较与讨论。
当上文描述的两个指标不能两全时, 总体来说, 我们倾向于使用“年轻但可靠”的化石进行标记, 因为其具有很好的系统发育解析度, 不容易产生错置, 尽管其未必能很好地代表整个类群的分化时间。如果在使用“年轻但可靠”化石的基础上再使用“古老但有风险”的化石进行标记, 节点年龄会有增大的趋势(Sauquet et al, 2012)。但这一结果并不代表“古老但有风险”的化石的放置是错误的, 因为其系统发育解析的准确性是不可知的。因此, 在进行标记之前, 应对相关类群的化石进行系统描述, 包括离群化石(outliers), 在此基础之上, 筛选标定使用的化石(Parham et al, 2012)。对于“古老但有风险”的化石, 建议在标记系统发育树基部的节点(如根节点)时使用, 并设置最大年龄限制(Sauquet et al, 2012)。反之, “年轻但可靠”的化石适合使用在系统发育树的冠部, 并且其年龄往往小于冠部节点的实际年龄。
对于一些化石稀缺的类群, 是否选择采用不可靠的化石进行节点标记是一个值得讨论的问题(Sanders & Lee, 2007)。一般情况下, 单个不可靠化石标记可能会导致一定的误差, 在极端情况下可能会导致其标记节点的年龄明显大于该节点未标记的情形。但是, 尽管某些化石的年龄信息并不可靠, 化石标记节点数量的增加仍然能够提高时间树的可靠性, 尤其是在根节点或近根节点没有化石标记的情况下(Duchêne et al, 2014; Nie et al, 2020)。因此, 建议同时计算不可靠化石标记和不标记两种情形, 进行比较与讨论, 并阐述采信其一的理由。
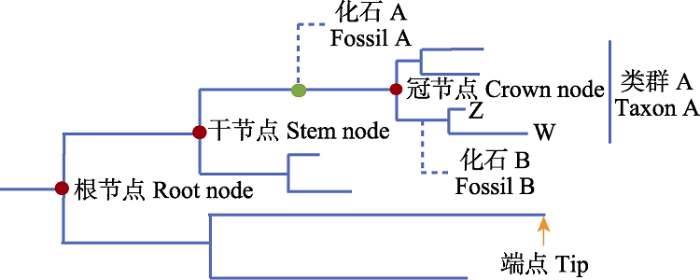
(2)标记节点选择。贝叶斯化石节点标记的第一步是将化石合理地放置于系统发育树中相应的节点或进化分支上, 主要包括直觉法(intuitive methods)、衍征法(apomorphy-based methods)和系统发育法(phylogenetic methods; Sauquet et al, 2012)。直觉法根据化石类群所能观测到的所有特征, 依靠直觉在现存类群中寻找与之最为相似的类群。该方法在早期研究中使用较多, 但由于其判断往往过于主观, 因此随着学科发展逐渐被弃用。衍征法依照化石与现存物种之间是否至少有一个共同衍征(synapomorphy)以及何时出现共同衍征进行化石位置放置的推断(Renner, 2005)。具有共同衍征的化石和现存物种聚为一个单系群, 并以化石年龄作为其干节点的最小年龄限制(图3)。但由于仅依靠共同衍征对化石关系进行判断, 该方法也存在一些缺陷, 例如趋同演化(convergent evolution)、衍征数量选择多少合适以及没有量化的数据分析(例如分子序列信息和形态学矩阵, morphological matrix) (Sauquet, 2013)。系统发育法则完全依赖系统发育分析重建化石类群与现存类群之间的关系, 在系统发育分析中同时使用现存类群和化石类群的数据集, 可以完全使用形态学数据, 也可以加入现存类群的分子序列数据进行分析(全证据法)。然而, 这三种化石关系的评估方法都是建立在化石拥有足够多的差异性形态特征的基础之上, 否则就无法得出有效的系统发育位置信息(Sauquet et al, 2012)。
图3
图3
系统发育树中部分术语示意图。图中冠节点的年龄代表了类群A现存所有物种最近共同祖先的节点, 而干节点代表了该类群最近共同祖先与其最近缘类群共祖的节点。以衍征法为例, 图中的化石A与类群A现存物种存在共同衍征, 因此可以作为类群A干节点的最小年龄限制; 而要为类群A的冠节点添加年龄限制, 需要获得与类群A的亚类群具有共同衍征的化石记录, 如图中的物种Z、W和化石B所表示的关系。系统发育法同理。
Fig. 3
Schematic diagram of some terms in phylogenetic tree. The age of the crown node in the figure represents the node of the nearest common ancestor of all species in group A, while the stem node represents the node of the nearest common ancestor of the group A and its nearest related group. Taking the apomorphy-based method as an example, fossil A in the figure has synapomorphies with the extant species of group A, so it can be used as the minimum age constraint for the stem node of group A. To apply age constraint to the crown node of group A, it is necessary to obtain fossil records sharing synapomorphies with subgroups of group A, as indicated by the relationship of species Z, W and fossil B in the figure. The same is true of phylogenetic method.
另一点需要注意的是, 在一棵系统发育树上确定一个类群的年龄时, 有冠年龄(crown age)与干年龄(stem age)之分: 前者代表该类群现存物种最近共同祖先的年龄, 而后者代表该类群最近共同祖先与其姊妹类群的最近共同祖先的年龄。不同的化石适用于不同的节点年龄类型。如图3所示, 无论是基于衍征法还是系统发育法进行化石放置, 位于类群干节点和冠节点之间的化石适合作为类群干节点的最小年龄限制, 位于亚类群干节点和冠节点之间的化石适合作为类群冠节点的最小年龄限制, 若使用介于类群干节点和冠节点之间的化石(基于最小年龄限制)标记冠节点往往导致节点年龄被高估(Parham et al, 2012)。另外, 因为化石标记点的定位几乎完全依赖形态学特征(Fikáček et al, 2020), 化石的完整性是合理确定化石位置的必要条件, 保存不完整、破碎程度高的化石很可能导致定位不准确, 从而对节点定年产生极大影响(Donoghue et al, 1989)。在实际操作中, 增加化石标记节点的数量以及尽量选用接近根节点的化石标记都会改善分化时间估计的可靠性(Duchêne et al, 2014)。
在研究大尺度系统发育时, 研究人员往往会进行非随机的、覆盖面广的现存类群取样, 但很可能忽略了一些亚类群(subclade)的取样(如一个大科或一个大属仅由少数物种代表), 导致得出的取样不全类群的冠节点年龄实际上为其亚类群的冠节点年龄(Magallón & Castillo, 2009), 从而导致年龄低估的现象。因此现存类群和相关化石的取样不仅应该使分支取样的覆盖面广, 在选择冠节点进行标记时还尤其需要对亚系(sublineage)、亚类群进行取样以保证准确性和代表性。已有研究表明, 化石类群和现存类群的取样覆盖度偏低都会导致低估节点年龄(Linder et al, 2005; Sauquet et al, 2012)。
此外, 依据节点之间的拓扑关系将有化石标记节点的年龄信息附加于无化石节点之上, 也是一种标记的策略。Barba-Montoya等(2017)使用了三种策略进行化石标记: (a)对无化石的节点不进行标记; (b)使用有化石节点的年龄上限、下限来标记相邻的无化石节点; (c)使用有化石节点的年龄上限、下限来标记所有其他节点, 这样所有的节点都有一对上下限的设置。结果表明, 方案(c)得到的年龄大于方案(b), 而(b)大于(a)。但目前来说, 这类标记策略的可靠性难以验证, 因此提高化石的采样频率才是提高定年准确度的根本途径。
2.3.2 二次标记
二次标记是在相应类群化石记录匮乏的情况下, 使用前人系统发育研究中已经得到的节点年龄或替换速率进行标定的方法。在实际操作中往往选择一个或多个节点进行二次标记, 或设置前人研究得出的替换速率作为先验。由于前人研究选择的标定策略未必一定合理、准确, 再者由于有更多新的化石被发现、化石年龄得到更新, 二次标记得到的节点年龄往往比化石标记得到的节点年龄年轻, 其导致的分支替换速率误差甚至能达到2到3倍之多(Sauquet et al, 2012)。因此二次标记不是最好的选择, 在相关类群有合适的化石的情况下应优先选择化石标记。如果确实需要使用二次标记, 应注意选择从最新发表或者化石标记相对合理的进化时间树上提取相应节点的年龄。另外, 因为标记节点的增加有助于提高整体时间计算的准确度(Conroy & van Tuinen, 2003; Marshall, 2008; Sauquet et al, 2012), 因此可以考虑采用多个节点进行二次标定。
2.3.3 使用生物地理学事件年龄进行标定
在没有合适的化石标记的情况下, 使用生物地理学事件发生的年代进行节点标记也是可行的方法之一。这往往涉及大陆与板块的运动, 例如澳大利亚与新西兰的分离可以解释某些物种的隔离分化事件(Martin & Dowd, 1993)。如果我们能知道两个地理区域较为准确的分离时间, 即某些地质事件年代, 就可以认为分别在两地分布的一对姊妹类群至少在地质事件发生后产生了分化, 换言之就知道了二者最近共同祖先节点年龄的下限。然而, 与化石标记相比, 这种方法无法考虑物种长距离扩散等由于扩散分布而非隔离分化产生的姊妹类群分化的情况, 因此这种情况下物种分化的实际时间常晚于地理事件年龄, 利用地理事件年龄标记得到的类群的物种分化时间往往比化石标记时间古老(高估) (Sauquet et al, 2012)。
2.3.4 其他节点标定和替换速率的信息来源
节点年龄标定的原理在于基于某种证据确定某一时间节点早于或晚于物种形成事件, 从而对物种形成时间进行限制。此处所述的证据包括但不限于化石标记、二次标记和地理隔离标记。其他的设置方法还有: (1)使用海洋岛屿形成时间作为该地特有种的年龄上限(Schaefer et al, 2009); (2)使用古DNA的年龄作为某一现存后代类群的时间先验(Korber et al, 2000); (3)使用宿主之间分化的年龄作为相应严格寄生物种之间分化的年龄上限(Rector et al, 2007)等。此外, 若使用其他研究得出的传代绝对替换速率作为速率先验, 就可以避免部分时间先验的设置。例如, 可以通过比较父代和子代之间的遗传差异计算出世代替换速率, 再除以世代时间就可得出绝对替换速率。但是, 除了模式物种与部分细菌(Kuo & Ochman, 2009)、病毒(Vijgen et al, 2005), 绝大多数类群的绝对替换速率往往难以获得(Sauquet, 2013)。
2.3.5 节点年龄概率分布的选择
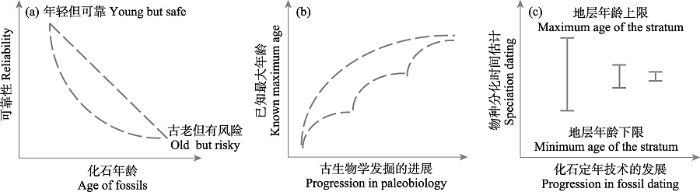
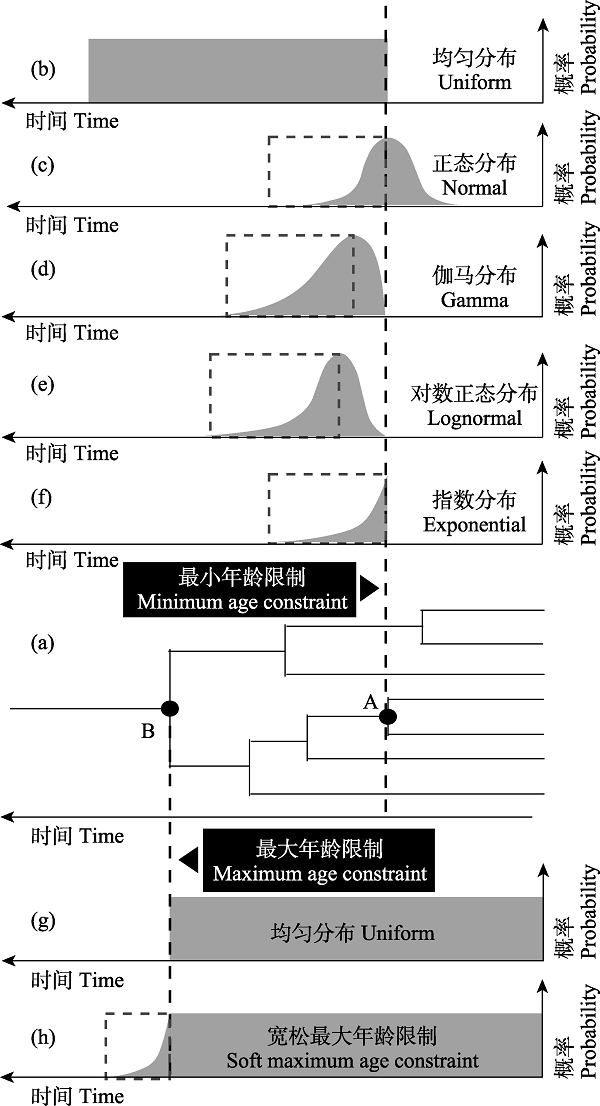
由于化石记录提供的年龄信息具有不确定性和时效性(图4), 在利用化石标记设置节点年龄时, 人们倾向于使用带有概率分布(probability distribution)的先验。概率分布允许节点的时间标记存在一定的误差, 体现了人类对化石信息的不确定性的认识。常见的概率分布有均匀分布(uniform)、对数正态分布(lognormal)、正态分布(normal)、指数分布(exponential)和伽马分布(Gamma)等(图5)。在此基础之上, 可以选择设置严格年龄限制(strict age constraint, 又称硬边界, hard bound)和宽松年龄限制(soft age constraint, 又称软边界, soft bound; Yang & Rannala, 2006)。宽松年龄限制允许存在一个较小的可能性(比如5%或10%), 使得节点年龄可以突破设定的边界(Yang & Rannala, 2006)。从实际角度出发, 人们目前获得某一类群最古老化石即为该类群实际上最古老化石的可能性几乎为零, 宽松年龄限制以及概率分布曲线可以为研究人员探究更加接近类群的真实年龄提供途径, 从而避免单一依赖其年龄下限(dos Reis et al, 2016)。通常对于非根部节点, 化石标记节点年龄的各类先验概率分布都可以设置一个严格的最小年龄限制(strict minimum age constraint), 表示化石的年龄绝对不小于这一年龄限制。严格最小年龄限制和宽松最大年龄限制(soft maximum age constraint; Benton & Donoghue, 2007)是节点定年中常用的设置组合。近年来, 除了对最大年龄设置宽松上限以外, 很多研究者还会对最小年龄也设置宽松下限(Barba-Montoya, 2017; Nie, 2020), 以减少其他因素带来的影响(如化石定年的误差)。在MCMCTree等软件中, 正态分布、伽马分布、对数正态分布和指数分布的内在逻辑都包含一个宽松最大年龄限制(图5c-f), 相应分布模型中年龄概率分布的参数可以由用户设置。不同的概率分布对节点年龄的影响有倾向性。
图4
图4
化石年龄不确定性的3种情形。(a)“年轻但可靠”和“古老但有风险”的两种化石在化石年龄和可靠性两个维度上的分布, 其他大多数化石分布于两虚线围成的区域中。(b)某个类群已知最古老化石的年龄随着古生物学发掘过程不断扩展补充、逐步接近类群真实分化时间的趋势。(c)随着化石定年技术的发展, 化石年龄的精确度不断提升。
Fig. 4
Three cases of fossil age uncertainty. (a) The present of “young but safe” and “old but risky” fossils in two dimensions: age of fossils and reliability. Most of the other fossils are distributed in the area surrounded by the two dotted lines. (b) The age of the oldest known fossil of a certain group tends to be close to the real divergence time of the group as the paleobiological excavation continues to expand. (c) With the development of fossil dating technology, the accuracy of fossil age has been improved.
图5
图5
节点年龄的概率分布。在不同节点设置最大或最小年龄限制, 可以采用不同的概率分布。其中(a)图表示系统发育树上设置最小和最大年龄限制的两个节点, (b)-(f)强调均匀、正态、伽马、对数正态和指数分布中的最小年龄限制, 而(g)和(h)则分别表示了均匀分布中的严格和宽松最大年龄限制(虚线及虚线框)。另外, (c)-(f)中虚线框强调的部分等同于宽松最大年龄限制。图中的soft maximum/minimum constraint又称软边界(soft bound)。
Fig. 5
Probability distribution of node age. The maximum or minimum age constraint can be set on different nodes, and different probability distribution can be adopted. Where (a) shows two nodes with minimum and maximum age constraint, respectively, in phylogenetic tree; (b)-(f) emphasize the minimum age constraints in uniform, normal, gamma, lognormal and exponential distribution, while (g) and (h) represent strict and relaxed maximum age constraints on uniform distribution, respectively. In addition, the part highlighted by the dotted box in (c)-(f) is equivalent to the relaxed maximum age constraint. The soft maximum/minimum constraint in the figure is also called soft bound.
与其他分布相比, 正态分布的特点是其允许双向的不确定性, 即节点年龄可能大于校准信息年龄, 也可能小于校准信息年龄。正态分布尤其适用于某些利用生物地理学证据进行标记的情况, 因为研究者往往无法确定遗传分化开始于地理隔离之前还是之后(Heads, 2005), 正态分布为这一问题的解决提供了可能。正态分布也适合于二次标记。
相对来讲, 对数正态分布是与古生物学研究现状较为匹配的一种先验设置(Ho & Phillips, 2009), 其包含3个参数: 均值、标准差和最小年龄限制。如图5所示, 对数正态分布允许节点的年龄概率峰值大于所用化石的年龄, 认为所用化石即为该类群最古老化石的可能性几乎为零(将当前化石年龄设置为最小年龄限制), 这与实际情况是吻合的。但其实际的均值仍然是未知的, 因此其设置难免主观、武断。过渡类群的化石适合使用对数正态分布, 因为这类化石在具有较好的系统发育解析度的同时, 其特征性状往往被认为是短时间内演化而来的, 因此能够对该类群的分化时间有较好的预测(作为均值进行设置; Slack et al, 2006)。此外, 有研究表明, 基于分子数据得到的节点年龄是对数正态分布的, 因此使用对数正态分布导入基于分子数据的二次标记能够考虑前人数据的误差(Ho & Phillips, 2009)。
伽马分布的表现形式与对数正态分布十分相似, 也包含3个参数: 形状指数(alpha)、尺度参数(beta)和最小年龄限制。其参数设置和适用条件可以参考对数正态分布。指数分布有2个参数: 均值和最小年龄限制。它是伽马分布的极端例子, 相比于伽马分布和对数正态分布少了一个参数的设置, 因此适用于化石信息不太完整的情况。在使用指数分布时, 研究者相信所使用的化石几乎就是该类群最古老的化石(Ho & Phillips, 2009)。
值得注意的是, “年轻但可靠”的化石适合使用均匀分布, 使其实质上仅发挥最小年龄限制的作用; 因为最小年龄现实标记某节点时, 其年龄上限存在很大的弹性空间, 同时施加一个宽松最大年龄限制(如对数正态分布、正态分布、指数分布和伽马分布等)可能会导致节点年龄的低估。同时, 在根节点可以考虑使用严格或者宽松最大年龄限制。为了避免节点年龄无限增大的可能性, 应至少对根节点进行最大年龄的限制。有研究表明, 在化石标记覆盖面广的情况下, 根节点的最大年龄限制的小幅波动对多数节点、尤其是冠部节点的影响十分有限(95%最高后验概率密度区间基本重叠; Mao et al, 2012)。最后, 在实际开展分子钟节点标记时, 强烈建议研究人员在论文的材料和方法部分提供详细、合理的依据以说明为什么每个化石标记节点选择相应的节点年龄概率分布。
3 解读贝叶斯节点标记分子钟估算节点年龄结果的建议
利用贝叶斯节点标记分子钟获得时间树之后, 应谨慎解读节点年龄, 建议基于节点年龄的贝叶斯可信区间(credible intervals)进行相关讨论, 并尽量避免使用节点年龄的均值进行讨论。一般来说, 分子钟估算软件产生的结果是由众多先验分布、模型参数和数据集共同作用得到的, 其中存在着若干未知参数的影响, 充满了不确定性。因此, 若仅用均值来讨论节点的年龄并不合适(Wang & Mao, 2016)。Crisp等(2011)的综述阐述了可信区间对于生物地理学假设检验的重要意义。例如, 假设某一对姊妹类群的分化是由于某一个地质事件而引发,则可比较姊妹类群分化时间的可信区间与地质事件发生时间二者之间是否存在显著差异。若存在显著差异, 可以拒绝该假设; 否则, 视为二者存在相关性, 不能拒绝该假设。置信区间(confidence intervals)和可信区间是频率学派与贝叶斯学派对同一问题的不同阐释, 其数值上的表现往往是相近的(Chen & Shao, 1999)。前者不能对参数的概率分布进行评估, 而后者可以。在模型单一(单峰)时, 贝叶斯可信区间等同于最高后验概率密度区间(highest posterior density (HPD) intervals)。
4 分子钟估算软件选择和使用的建议
使用贝叶斯化石节点标记法进行物种分化时间估算可以分为两大类: 一类采用先建树后定年的方法, 即先构建具有拓扑的系统发育树, 然后利用化石对节点定年得出绝对分化时间树, MultiDivTime、PAML-MCMCTree等软件使用的就是此类方法, 其优点是速度快(Ho & Duchêne, 2014); 另一类方法则同时进行建树和定年, 其运行速度慢, 但在定年时能充分考虑系统发育树拓扑的不确定性(Sauquet, 2013), BEAST、MrBayes等软件主要使用的就是此类方法(各类软件的功能及内置模型可见参考文献: Ho & Duchêne, 2014)。化石标记的各类先验和参数设定引入的不确定性可能引起系统发育树结构差异, 因此在时间和计算资源充裕的情况下, 使用同时建树和定年的方法, 可以提高构建系统发育树结构的准确性; 但在分子数据量或类群数量过多时, 由于其模型过于复杂, 可能使得同时建树和定年方法的MCMC链收敛困难。与之相比, 只要数据集的信息量足够大, 先建树后定年的方法不会对系统发育树的拓扑产生影响(Ho & Phillips, 2009), 因此目前利用全基因组水平数据构建时间树时通常使用此类软件, 如PAML-MCMCTree等(朱天琪, 2019)。
下面以BEAST v1.10.4软件为例介绍同时建树和定年类软件的使用。用户需首先在BEAUti软件中对进化模型参数进行设置, 在BEAUti主界面中可见到Partitions、Taxa、Tips、Traits、Sites、Clocks、Trees、States、Priors、Operators、MCMC等分界面, 其具体设置可参考本文各章节给出的建议。需要注意的是, 在Clocks分界面中, 除了对数、指数等常规分布外还可以选择“模型平均化”(model averaging), 能够对多个松弛模型进行平均化, 这在对分子钟模型的选择难以决断时十分实用(Duchêne et al, 2014)。在Trees界面中可以对树模型和树先验进行设置, 树模型既可以通过BEAST软件自动计算得出的树作为起始树(starting tree; 随机选取的树或使用UPGMA算法的树), 也可以导入NEXUS格式的树文件作为起始树。在MCMC分界面中除了可以设置MCMC链的长度等参数外, 还可以选择评估边缘似然值的方法(marginal likelihood estimation), 用于后续的模型比较。此后, 将BEAUti生成的XML文件作为输入文件导入BEAST软件并运算。得到的结果可以用Tracer软件查看, 包括后验及其他各参数的均值、标准差、95%HPD等。
关于BEAST软件使用的入门指南和释疑文档很多, 例如BEAST软件官方网站的使用指南(Suchard et al, 2018)、福建农林大学高芳銮科学网博客相关博文(
随着基因组学与测序技术的发展, 用全基因组数据建立时间树的方法逐渐得到广泛认可, 这要求计算机具有较强的计算能力、软件算法更加精巧且具有较快计算速度。MCMCTree是PAML 4 (Yang, 2007)中的软件包, 与BEAST一样支持多种分子钟模型、核酸替换模型和年龄先验分布, 支持节点标记和端点标记的设置, 使用时需要用户提供一棵系统发育树, 属于先建树后定年类方法。该软件最大的优势在于可以选择快速近似似然法(fast approximate likelihood)对时间树进行计算评估, 该方法效率高并且占用计算资源小, 在利用数据量庞大的基因组进行贝叶斯物种分化时间估计时, 可极大提高运算速度。与BEAST的可视化界面不同, MCMCTree软件目前没有可视化界面, 需输入代码进行运算。此外, 由于计算中涉及密码子的3个位点, 因此不建议使用氨基酸序列进行计算。软件详细操作可见PAML4官方说明文件(
5 不同模型、先验设置得到的贝叶斯时间树的比较方法
贝叶斯因子(Bayes factor)是检测两个模型间有无显著差异的统计量。在比较贝叶斯节点分子钟定年方法中两个不同的模型得出的时间树时, 主流的比较方法都需要计算贝叶斯因子(Sinsheimer et al, 1996; Suchard et al, 2001), 计算公式如下(Jeffreys, 1935):
其中, 贝叶斯因子B10是模型M1 (备择假设, alternative hypothesis)与模型M0 (零假设, null hypothesis的边缘似然值(marginal likelihood)之比, p(Y|M1)和p(Y|M0)分别是给定模型M1和M0后, 数据集Y的边缘似然值(具体数学阐述可见参考文献: Good & Hardin, 2012)。利用贝叶斯因子检验模型的参数设置, 相当于回答下列问题: 基于给定数据集计算时间树时, 零假设(相比于备择假设的特定参数设置的差异)的可信度(credibility)是否更高?当被运用于模型比较时, 给出的数据集在哪个模型中更加有可能出现?
从20世纪90年代开始, 对贝叶斯法时间树构建模型进行评估的统计方法层出不穷, 具有深远影响的包括调和平均估计量(harmonic mean estimator, HME; Newton & Raftery, 1994)、赤池信息量准则(Akaike’s information criterion, AIC; Raftery et al, 2006)、路径抽样(path sampling, PS; Lartillot & Philippe, 2006)、垫脚石抽样(stepping-stone sampling, SS; Xie et al, 2011)、广义垫脚石抽样(generalized stepping-stone sampling; Fan et al, 2011)等。这些方法和估计量都致力于解决边缘似然值的复杂计算问题。HME法与AIC法由于表现不佳(Lartillot & Philippe, 2006; Xie et al, 2011; Baele et al, 2012a), 其使用频率逐渐降低, 而准确度更高的PS、SS等方法则为BEAST等主流贝叶斯系统发育分析软件所采纳运用, 从而得到更好的推广(Baele et al, 2012b)。
除了主流的贝叶斯因子模型比较法以外, 还可以利用使用频率相对较低的一些基于其他因子进行的模型评估方法。例如Wagenmakers等(2020)提出了支持区间(support interval)的概念, 其所衡量的是“给定数据集对观测者的预设产生了多大的影响”。在该方法中, 贝叶斯因子是一个主观设定的参数, 表现了研究者对支持区间呈现范围的预期, 该方法已应用于bayestestR软件(Makowski et al, 2019)。另外, Duchêne等(2017)提出了标准差预测距离(stand deviation predictive distance, SDPD)来更准确地衡量模型间差异的信号。然而, 相比于主流的比较方法, 这些新兴的贝叶斯模型比较方法有待进一步检验。
有时不同的因子(如贝叶斯因子和支持区间)或者不同的计算方法对模型的支持倾向有所不同, 需要综合考虑。Van den Bergh等(2021)认为, 当不同评估参数对模型的评估结果差异较大时, 不必拘泥于选择某一个模型或参数进行评估, 而可以对两者的后验概率取均值(根据边缘似然值加权), 获得联合后验概率。在现实的系统发育分析中, 依照研究的需求, 模型与实际数据集并不一定要保证100%符合, 而应该在简洁高效与数据的绝对真实性之间寻求平衡, 从而更好地揭示数据的关键特征(Steel, 2005)。
6 总结
贝叶斯节点标记法中的不确定性因素有很多, 初学者宜遵循每一个步骤和每一个参数设置都有据可循(如参考文献支持)的原则来尽量控制不确定性。我们将提高贝叶斯节点标记法可靠性的建议归纳为以下几点:
(1)对于不同的替换模型、分子钟模型和先验设置(尤其是化石标记节点年龄的先验设置)的选择要慎重, 对于争议较大的情况, 最好分别按照不同的模型设置和参数设置对实际数据进行分析, 并基于贝叶斯因子等对结果进行统计分析和横向对比, 选择最优的模型和参数设置进行最终分析(Ho & Duchêne, 2014)。在此基础上, 研究者应立足于所研究的案例, 针对上述争议提出相应意见与观点, 从而为相应类群乃至相应领域的研究提供改进建议, 进而不断提高节点标记的准确度和精密度(Parham et al, 2012)。例如, 随着分子数据量的增加, 应尽量使用宽松分子钟模型而避免使用严格分子钟模型(Ho & Duchêne, 2014)。其他不同的情况下模型与化石标记的使用导致的年龄估算偏差, 可参见相关参考文献(Wang & Mao, 2016; Sauquet et al, 2012; Shapiro et al, 2006; Wu et al, 2013; Warnock et al, 2017)。
(2)在年龄标记信息准确可靠的基础上, 可以尽量采用多重标记(multi-calibration)进行时间校准。例如, 对多个节点进行化石标记, 整合使用具有时间异质性(heterochronous)的序列数据(如古DNA或不同时期的病毒序列)等(Ho & Duchêne, 2014)。有研究表明, 总体上年龄标记数量越多, 节点定年越准确(Conroy & van Tuinen, 2003), 但须尽量保证这些标记年龄是相对准确可靠的(Ho & Duchêne, 2014)。
(3)在开展化石标记时, 应仔细收集和比较与目标类群相关的化石, 详细阐述重要的化石类群, 在考虑到主要化石类群的优缺点的基础上, 选择合适的化石类群开展化石标记。最好能够与古生物学家和分类学家合作, 由其依据已有的、广泛接受的化石标记原则, 系统、严谨地描述和选择化石类群, 并根据形态学矩阵利用系统发育方法重建现存类群和化石类群之间的系统发育关系, 从而更合理、更客观地确定化石标定的节点位置(Parham et al, 2012)。对于引起时间估算争议的关键化石可以分别计算有(激进)、无(保守)两种情况, 并进行比较与深入讨论。
(4)应注意更新化石信息(尤其是埋藏点的最新定年年龄), 并不断更新分子钟定年方法(Parham et al, 2012)。若新发现的化石与以前发表的分子钟定年方法得出的时间树不一致, 不应急于否定分子钟定年方法(Wilf & Escapa, 2015), 而应该不断整合最新发现的、年龄更古老的化石类群作为标记信息, 更新相应类群的时间树(Parham et al, 2012; Wang & Mao, 2016)。虽然化石记录是绝大多数生物类群获取绝对分化时间的唯一可靠来源, 但是化石记录本身是一个不断动态更新、具有时效性的集合(图4), 而特定时间发表的、基于当时化石记录利用分子钟得出的时间树, 也同样具有时效性; 因此, 新发现的化石记录对过去化石记录的否定, 只代表对信息时效性的否定与更新, 而不能将现有化石与以前发表的、分子钟得出的时间树之间的不一致性, 作为证据否定分子钟定年方法, 否则便落入了诡辩的循环。
(5)由于各种先验和分子数据的复杂相互作用, 在讨论进化分支分化时间时, 应尽量使用贝叶斯可信区间和最高后验密度区间, 避免使用均值。因为贝叶斯可信区间和最高后验密度区间代表了整个贝叶斯分子钟估算过程中的各类不确定性, 而均值则无法体现。
(6)在条件允许的情况下, 应选择不同类型的贝叶斯方法(节点标记法、全证据法、化石生灭进程等)估算时间树并比较不同方法得出的重要节点的估算年龄。近年来部分软件支持同时使用节点标记和端点标记, 并且已有研究表明二者并不冲突且可优势互补, 从而可以提高节点年龄的准确度和可信度(O’Reilly et al, 2015; O’Reilly & Donoghue, 2016)。需要注意的是, 在软件内开展化石标记时, 可以进行两类方法单独或者混合使用的比较, 尝试不同组合并择优采纳, 但择优时不宜主观, 应有统计学数据支持(如计算与比较贝叶斯因子)。
总之, 利用分子钟定年方法估算进化时间框架的要义在于从不确定性中寻找确定性, 不断更新化石记录与分子钟定年方法, 从而无限接近于真理, 即真实发生的、地球生物多样性产生的进化时间框架。
致谢
本文主要框架出自2018年第三届生物系统学大会上通讯作者题为“关于提升主流分子钟方法可靠性的建议”的学术报告。感谢中国科学院微生物研究所蔡磊老师和大会组委会的邀请。
参考文献
Improving the accuracy of demographic and molecular clock model comparison while accommodating phylogenetic uncertainty
DOI:10.1093/molbev/mss084
PMID:22403239
[本文引用: 1]

Recent developments in marginal likelihood estimation for model selection in the field of Bayesian phylogenetics and molecular evolution have emphasized the poor performance of the harmonic mean estimator (HME). Although these studies have shown the merits of new approaches applied to standard normally distributed examples and small real-world data sets, not much is currently known concerning the performance and computational issues of these methods when fitting complex evolutionary and population genetic models to empirical real-world data sets. Further, these approaches have not yet seen widespread application in the field due to the lack of implementations of these computationally demanding techniques in commonly used phylogenetic packages. We here investigate the performance of some of these new marginal likelihood estimators, specifically, path sampling (PS) and stepping-stone (SS) sampling for comparing models of demographic change and relaxed molecular clocks, using synthetic data and real-world examples for which unexpected inferences were made using the HME. Given the drastically increased computational demands of PS and SS sampling, we also investigate a posterior simulation-based analogue of Akaike's information criterion (AIC) through Markov chain Monte Carlo (MCMC), a model comparison approach that shares with the HME the appealing feature of having a low computational overhead over the original MCMC analysis. We confirm that the HME systematically overestimates the marginal likelihood and fails to yield reliable model classification and show that the AICM performs better and may be a useful initial evaluation of model choice but that it is also, to a lesser degree, unreliable. We show that PS and SS sampling substantially outperform these estimators and adjust the conclusions made concerning previous analyses for the three real-world data sets that we reanalyzed. The methods used in this article are now available in BEAST, a powerful user-friendly software package to perform Bayesian evolutionary analyses.
Accurate model selection of relaxed molecular clocks in Bayesian phylogenetics
DOI:10.1093/molbev/mss243 URL [本文引用: 1]
Comparison of different strategies for using fossil calibrations to generate the time prior in Bayesian molecular clock dating
DOI:S1055-7903(17)30304-4
PMID:28709986
[本文引用: 3]

Fossil calibrations are the utmost source of information for resolving the distances between molecular sequences into estimates of absolute times and absolute rates in molecular clock dating analysis. The quality of calibrations is thus expected to have a major impact on divergence time estimates even if a huge amount of molecular data is available. In Bayesian molecular clock dating, fossil calibration information is incorporated in the analysis through the prior on divergence times (the time prior). Here, we evaluate three strategies for converting fossil calibrations (in the form of minimum- and maximum-age bounds) into the prior on times, which differ according to whether they borrow information from the maximum age of ancestral nodes and minimum age of descendent nodes to form constraints for any given node on the phylogeny. We study a simple example that is analytically tractable, and analyze two real datasets (one of 10 primate species and another of 48 seed plant species) using three Bayesian dating programs: MCMCTree, MrBayes and BEAST2. We examine how different calibration strategies, the birth-death process, and automatic truncation (to enforce the constraint that ancestral nodes are older than descendent nodes) interact to determine the time prior. In general, truncation has a great impact on calibrations so that the effective priors on the calibration node ages after the truncation can be very different from the user-specified calibration densities. The different strategies for generating the effective prior also had considerable impact, leading to very different marginal effective priors. Arbitrary parameters used to implement minimum-bound calibrations were found to have a strong impact upon the prior and posterior of the divergence times. Our results highlight the importance of inspecting the joint time prior used by the dating program before any Bayesian dating analysis.Copyright © 2017 The Authors. Published by Elsevier Inc. All rights reserved.
Comparison of Bayesian and maximum- likelihood inference of population genetic parameters
Comparison of the performance and accuracy of different inference methods, such as maximum likelihood (ML) and Bayesian inference, is difficult because the inference methods are implemented in different programs, often written by different authors. Both methods were implemented in the program MIGRATE, that estimates population genetic parameters, such as population sizes and migration rates, using coalescence theory. Both inference methods use the same Markov chain Monte Carlo algorithm and differ from each other in only two aspects: parameter proposal distribution and maximization of the likelihood function. Using simulated datasets, the Bayesian method generally fares better than the ML approach in accuracy and coverage, although for some values the two approaches are equal in performance.The Markov chain Monte Carlo-based ML framework can fail on sparse data and can deliver non-conservative support intervals. A Bayesian framework with appropriate prior distribution is able to remedy some of these problems.The program MIGRATE was extended to allow not only for ML(-) maximum likelihood estimation of population genetics parameters but also for using a Bayesian framework. Comparisons between the Bayesian approach and the ML approach are facilitated because both modes estimate the same parameters under the same population model and assumptions.
Paleontological evidence to date the tree of life
DOI:10.1093/molbev/msl150 URL [本文引用: 1]
BEAST 2: A software platform for Bayesian evolutionary analysis
DOI:10.1371/journal.pcbi.1003537 URL [本文引用: 1]
bModelTest: Bayesian phylogenetic site model averaging and model comparison
DOI:10.1186/s12862-017-0890-6
PMID:28166715
[本文引用: 1]

Background: Reconstructing phylogenies through Bayesian methods has many benefits, which include providing a mathematically sound framework, providing realistic estimates of uncertainty and being able to incorporate different sources of information based on formal principles. Bayesian phylogenetic analyses are popular for interpreting nucleotide sequence data, however for such studies one needs to specify a site model and associated substitution model. Often, the parameters of the site model is of no interest and an ad- hoc or additional likelihood based analysis is used to select a single site model.Results: bModelTest allows for a Bayesian approach to inferring and marginalizing site models in a phylogenetic analysis. It is based on trans- dimensional Markov chain Monte Carlo (MCMC) proposals that allow switching between substitution models as well as estimating the posterior probability for gamma- distributed rate heterogeneity, a proportion of invariable sites and unequal base frequencies. The model can be used with the full set of time- reversible models on nucleotides, but we also introduce and demonstrate the use of two subsets of time- reversible substitution models.Conclusion: With the new method the site model can be inferred (and marginalized) during the MCMC analysis and does not need to be pre- determined, as is now often the case in practice, by likelihood- based methods. The method is implemented in the bModelTest package of the popular BEAST 2 software, which is open source, licensed under the GNU Lesser General Public License and allows joint site model and tree inference under a wide range of models.
An empirical assessment of long-branch attraction artefacts in deep eukaryotic phylogenomics
DOI:10.1080/10635150500234609 URL [本文引用: 1]
Bayesian molecular dating: Opening up the black box
DOI:10.1111/brv.2018.93.issue-2 URL [本文引用: 3]
Quantitative phylogenetic analysis in the 21st century
Statistical consistency and phylogenetic inference: A brief review
DOI:10.1111/cla.2018.34.issue-5 URL [本文引用: 1]
Rate variation and estimation of divergence times using strict and relaxed clocks
DOI:10.1186/1471-2148-11-271 URL [本文引用: 2]
Monte Carlo estimation of Bayesian credible and HPD intervals
A new time tree reveals Earth history’s imprint on the evolution of modern birds
DOI:10.1126/sciadv.1501005 URL [本文引用: 1]
Origin and diversification of living cycads: A cautionary tale on the impact of the branching process prior in Bayesian molecular dating
DOI:10.1186/s12862-014-0274-0 URL [本文引用: 2]
Extracting time from phylogenies: Positive interplay between fossil and genetic data
DOI:10.1644/1545-1542(2003)084<0444:ETFPPI>2.0.CO;2 URL [本文引用: 2]
A cautionary note on the use of Ornstein Uhlenbeck models in macroevolutionary studies
DOI:10.1111/bij.2016.118.issue-1 URL [本文引用: 1]
Hypothesis testing in biogeography
DOI:10.1016/j.tree.2010.11.005 URL [本文引用: 1]
jModelTest 2: More models, new heuristics and parallel computing
DOI:10.1038/nmeth.2109 PMID:22847109 [本文引用: 1]
The importance of fossils in phylogeny reconstruction
DOI:10.1146/annurev.es.20.110189.002243 URL [本文引用: 1]
Toward an integrative historical biogeography
DOI:10.1093/icb/43.2.261 URL [本文引用: 1]
Bayesian molecular clock dating of species divergences in the genomics era
DOI:10.1038/nrg.2015.8 URL [本文引用: 2]
Phylogenomic datasets provide both precision and accuracy in estimating the timescale of placental mammal phylogeny
Uncertainty in the timing of origin of animals and the limits of precision in molecular timescales
DOI:10.1016/j.cub.2015.09.066 URL [本文引用: 1]
Relaxed phylogenetics and dating with confidence
DOI:10.1371/journal.pbio.0040088 URL [本文引用: 1]
Bayesian phylogenetics with BEAUti and the BEAST 1.7
DOI:10.1093/molbev/mss075
PMID:22367748
[本文引用: 1]

Computational evolutionary biology, statistical phylogenetics and coalescent-based population genetics are becoming increasingly central to the analysis and understanding of molecular sequence data. We present the Bayesian Evolutionary Analysis by Sampling Trees (BEAST) software package version 1.7, which implements a family of Markov chain Monte Carlo (MCMC) algorithms for Bayesian phylogenetic inference, divergence time dating, coalescent analysis, phylogeography and related molecular evolutionary analyses. This package includes an enhanced graphical user interface program called Bayesian Evolutionary Analysis Utility (BEAUti) that enables access to advanced models for molecular sequence and phenotypic trait evolution that were previously available to developers only. The package also provides new tools for visualizing and summarizing multispecies coalescent and phylogeographic analyses. BEAUti and BEAST 1.7 are open source under the GNU lesser general public license and available at http://beast-mcmc.googlecode.com and http://beast.bio.ed.ac.uk.
New statistical criteria detect phylogenetic bias caused by compositional heterogeneity
DOI:10.1093/molbev/msx092
PMID:28333201

In statistical phylogenetic analyses of DNA sequences, models of evolutionary change commonly assume that base composition is stationary through time and across lineages. This assumption is violated by many data sets, but it is unclear whether the magnitude of these violations is sufficient to mislead phylogenetic inference. We investigated the impacts of compositional heterogeneity on phylogenetic estimates using a method for assessing model adequacy. Based on a detailed simulation study, we found that common frequentist criteria are highly conservative, such that the model is often rejected when the phylogenetic estimates do not show clear signs of bias. We propose new criteria and provide guidelines for their usage. We apply these criteria to genome-scale data from 40 birds and find that loci with severely non-homogeneous base composition are uncommon. Our results show the importance of using well-informed diagnostic statistics when testing model adequacy for phylogenomic analyses.© The Author 2017. Published by Oxford University Press on behalf of the Society for Molecular Biology and Evolution. All rights reserved. For permissions, please e-mail: journals.permissions@oup.com.
The impact of calibration and clock-model choice on molecular estimates of divergence times
DOI:10.1016/j.ympev.2014.05.032 URL [本文引用: 4]
Choosing among partition models in Bayesian phylogenetics
DOI:10.1093/molbev/msq224
PMID:20801907
[本文引用: 1]

Bayesian phylogenetic analyses often depend on Bayes factors (BFs) to determine the optimal way to partition the data. The marginal likelihoods used to compute BFs, in turn, are most commonly estimated using the harmonic mean (HM) method, which has been shown to be inaccurate. We describe a new more accurate method for estimating the marginal likelihood of a model and compare it with the HM method on both simulated and empirical data. The new method generalizes our previously described stepping-stone (SS) approach by making use of a reference distribution parameterized using samples from the posterior distribution. This avoids one challenging aspect of the original SS method, namely the need to sample from distributions that are close (in the Kullback-Leibler sense) to the prior. We specifically address the choice of partition models and find that using the HM method can lead to a strong preference for an overpartitioned model. In contrast to the HM method and the original SS method, we show using simulated data that the generalized SS method is strikingly more precise (repeatable BF values of the same data and partition model) and yields BF values that are much more reasonable than those produced by the HM method. Comparisons of HM and generalized SS methods on an empirical data set demonstrate that the generalized SS method tends to choose simpler partition schemes that are more in line with expectation based on inferred patterns of molecular evolution. The generalized SS method shares with thermodynamic integration the need to sample from a series of distributions in addition to the posterior. Such dedicated path-based Markov chain Monte Carlo analyses appear to be a cost of estimating marginal likelihoods accurately.
Evolutionary trees from DNA sequences: A maximum likelihood approach
DOI:10.1007/BF01734359 URL [本文引用: 1]
Reliable placement of beetle fossils via phylogenetic analyses—Triassic Leehermania as a case study (Staphylinidae or Myxophaga?)
DOI:10.1111/syen.v45.1 URL [本文引用: 3]
On hyperpriors and hypopriors: Comment on Pellicano and Burr
DOI:10.1016/j.tics.2012.11.003 PMID:23218940 [本文引用: 1]
Common Errors in Statistics (and How to Avoid Them)
Measuring cancer evolution from the genome
DOI:10.1002/path.2017.241.issue-2 URL [本文引用: 1]
Using more than the oldest fossils: Dating Osmundaceae with three Bayesian clock approaches
DOI:10.1093/sysbio/syu108 URL [本文引用: 2]
Assessment of available anatomical characters for linking living mammals to fossil taxa in phylogenetic analyses
DOI:10.1098/rsbl.2015.1003 URL [本文引用: 1]
Comparison of the accuracies of several phylogenetic methods using protein and DNA sequences
DOI:10.1093/molbev/msi066 URL [本文引用: 1]
The impact of phylogenetic dating method on interpreting trait evolution: A case study of Cretaceous-Palaeogene eutherian body-size evolution
DOI:10.1098/rsbl.2016.0051 URL [本文引用: 1]
Cretaceous records of diatom evolution, radiation, and expansion
DOI:10.1017/S1089332600001455 URL [本文引用: 1]
Dating of the human-ape splitting by a molecular clock of mitochondrial DNA
DOI:10.1007/BF02101694 URL [本文引用: 1]
Dating nodes on molecular phylogenies: A critique of molecular biogeography
DOI:10.1111/cla.2005.21.issue-1 URL [本文引用: 1]
The fossilized birth-death process for coherent calibration of divergence- time estimates
Molecular-clock methods for estimating evolutionary rates and timescales
DOI:10.1111/mec.12953 URL [本文引用: 12]
Accounting for calibration uncertainty in phylogenetic estimation of evolutionary divergence times
DOI:10.1093/sysbio/syp035 URL [本文引用: 4]
RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language
DOI:10.1093/sysbio/syw021 URL [本文引用: 1]
Some tests of significance, treated by the theory of probability
Assessment of methods for amino acid matrix selection and their use on empirical data shows that ad hoc assumptions for choice of matrix are not justified
DOI:10.1186/1471-2148-6-29 URL [本文引用: 1]
A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences
DOI:10.1007/BF01731581 URL [本文引用: 1]
Timing the ancestor of the HIV-1 pandemic strains
DOI:10.1126/science.288.5472.1789 URL [本文引用: 1]
Molecular clocks: Four decades of evolution
DOI:10.1038/nrg1659 URL [本文引用: 1]
Advances in time estimation methods for molecular data
DOI:10.1093/molbev/msw026 URL [本文引用: 1]
Inferring clocks when lacking rocks: The variable rates of molecular evolution in bacteria
DOI:10.1186/1745-6150-4-35 URL [本文引用: 1]
PartitionFinder: Combined selection of partitioning schemes and substitution models for phylogenetic analyses
DOI:10.1093/molbev/mss020
PMID:22319168
[本文引用: 1]

In phylogenetic analyses of molecular sequence data, partitioning involves estimating independent models of molecular evolution for different sets of sites in a sequence alignment. Choosing an appropriate partitioning scheme is an important step in most analyses because it can affect the accuracy of phylogenetic reconstruction. Despite this, partitioning schemes are often chosen without explicit statistical justification. Here, we describe two new objective methods for the combined selection of best-fit partitioning schemes and nucleotide substitution models. These methods allow millions of partitioning schemes to be compared in realistic time frames and so permit the objective selection of partitioning schemes even for large multilocus DNA data sets. We demonstrate that these methods significantly outperform previous approaches, including both the ad hoc selection of partitioning schemes (e.g., partitioning by gene or codon position) and a recently proposed hierarchical clustering method. We have implemented these methods in an open-source program, PartitionFinder. This program allows users to select partitioning schemes and substitution models using a range of information-theoretic metrics (e.g., the Bayesian information criterion, akaike information criterion [AIC], and corrected AIC). We hope that PartitionFinder will encourage the objective selection of partitioning schemes and thus lead to improvements in phylogenetic analyses. PartitionFinder is written in Python and runs under Mac OSX 10.4 and above. The program, source code, and a detailed manual are freely available from www.robertlanfear.com/partitionfinder.
Computing Bayes factors using thermodynamic integration
DOI:10.1080/10635150500433722 URL [本文引用: 2]
Fifty Plants that Changed the Course of History
Multiple morphological clocks and total-evidence tip-dating in mammals
DOI:10.1098/rsbl.2016.0033 URL [本文引用: 1]
Continuous and tractable models for the variation of evolutionary rates
DOI:10.1016/j.mbs.2005.11.002 URL [本文引用: 1]
Quantitative analysis of relationship between absolute evolutionary rates and taxa divergence times
分子绝对进化速率与物种分歧时间之间的定量关系
Taxon sampling effects in molecular clock dating: An example from the African Restionaceae
DOI:10.1016/j.ympev.2004.12.006 URL [本文引用: 1]
The basic principle and application of the molecular clock hypothesis
分子钟假说的基本原理及在古生物等学科中的应用
Tree of life and its applications
DOI:10.3724/SP.J.1003.2014.13170 URL [本文引用: 2]
生命之树及其应用
Angiosperm diversification through time
DOI:10.3732/ajb.0800060 URL [本文引用: 1]
bayestestR: Describing effects and their uncertainty, existence and significance within the Bayesian framework
DOI:10.21105/joss URL [本文引用: 1]
Distribution of living Cupressaceae reflects the breakup of Pangea
A simple method for bracketing absolute divergence times on molecular phylogenies using multiple fossil calibration points
DOI:10.1086/587523
PMID:18462127
[本文引用: 2]

A central challenge facing the temporal calibration of molecular phylogenies is finding a quantitative method for estimating maximum age constraints on lineage divergence times. Here, I provide such a method. This method requires an ultrametric tree generated without reference to the fossil record. Exploiting the fact that the relative branch lengths on the ultrametric tree are proportional to time, this method identifies the lineage with the greatest proportion of its true temporal range covered by the fossil record. The oldest fossil of this calibration lineage is used as the minimum age constraint. The maximum age constraint is obtained by adding a confidence interval onto the end point of the calibration lineage, thus making it possible to bracket the true divergence times of all lineages on the tree. The approach can also identify fossils that have been grossly misdated or misassigned to the phylogeny. The method assumes that the relative branch lengths on the ultrametric tree are accurate and that fossilization is random. The effect of violations of these assumptions is assessed. This method is simple to use and is illustrated with a reanalysis of Near et al.'s turtle data.
Using sequences of rbcL to study phylogeny and biogeography of Nothofagus species
DOI:10.1071/SB9930441 URL [本文引用: 1]
Phylogeny and classification of whirligig beetles (Coleoptera: Gyrinidae): Relaxed-clock model outperforms parsimony and time-free Bayesian analyses
DOI:10.1111/sen.2012.37.issue-4 URL [本文引用: 1]
Emile Zuckerkandl, Linus Pauling, and the molecular evolutionary clock, 1959-1965
Approximate Bayesian inference with the weighted likelihood bootstrap. Journal of the Royal Statistical Society:
Accounting for uncertainty in the evolutionary timescale of green plants through clock-partitioning and fossil calibration strategies
DOI:10.1093/sysbio/syz032 URL [本文引用: 2]
Dating tips for divergence-time estimation
DOI:10.1016/j.tig.2015.08.001 URL [本文引用: 1]
Tips and nodes are complementary not competing approaches to the calibration of molecular clocks
DOI:10.1098/rsbl.2015.0975 URL [本文引用: 1]
Best practices for justifying fossil calibrations
DOI:10.1093/sysbio/syr107 PMID:22105867 [本文引用: 7]
Molecular paleontology
Estimating the integrated likelihood via posterior simulation using the harmonic mean identity
Ancient papillomavirus-host co-speciation in Felidae
Relaxed molecular clocks for dating historical plant dispersal events
DOI:10.1016/j.tplants.2005.09.010 URL [本文引用: 1]
Long-branch attraction phenomenon and the impact of among-site rate variation on rodent phylogeny
The phylogenetic relationships among major lineages of rodents is one of the issues most debated by both paleontologists and molecular biologists. In the present study, we have analyzed all complete mammalian mitochondrial genomes available in the databases, including five rodent species (rat, mouse, dormouse, squirrel and guinea-pig). Phylogenetic analyses were performed on H-strand amino acid sequences by means of maximum-likelihood and on H-strand protein-coding and ribosomal genes by means of distance methods. Also, log-likelihood ratio tests were applied to different tree topologies under the assumption of rodent monophyly, paraphyly or polyphyly. The analyses significantly rejected rodent monophyly and showed the existence of two differentiated clades, one containing non-murids (dormouse, squirrel and guinea-pig) and the other containing murids (rat and mouse). Long-branch attraction between murids and the outgroups could not be responsible for the existence of two different rodent clades, as no significant differences in evolutionary rate have been observed, except in the case of the squirrel, which shows a lower rate. The impact of among-site rate variation models on the phylogeny of rodents has been evaluated using the gamma distribution model. Results have shown that relationships among rodents remained unchanged, and the general topology of the tree was not affected, even though some branches were not properly resolved, most likely due to a lack of fit between estimated and real rate heterogeneity parameters.
A total-evidence approach to dating with fossils, applied to the early radiation of the Hymenoptera
DOI:10.1093/sysbio/sys058
PMID:22723471
[本文引用: 3]

Phylogenies are usually dated by calibrating interior nodes against the fossil record. This relies on indirect methods that, in the worst case, misrepresent the fossil information. Here, we contrast such node dating with an approach that includes fossils along with the extant taxa in a Bayesian total-evidence analysis. As a test case, we focus on the early radiation of the Hymenoptera, mostly documented by poorly preserved impression fossils that are difficult to place phylogenetically. Specifically, we compare node dating using nine calibration points derived from the fossil record with total-evidence dating based on 343 morphological characters scored for 45 fossil (4--20 complete) and 68 extant taxa. In both cases we use molecular data from seven markers (∼5 kb) for the extant taxa. Because it is difficult to model speciation, extinction, sampling, and fossil preservation realistically, we develop a simple uniform prior for clock trees with fossils, and we use relaxed clock models to accommodate rate variation across the tree. Despite considerable uncertainty in the placement of most fossils, we find that they contribute significantly to the estimation of divergence times in the total-evidence analysis. In particular, the posterior distributions on divergence times are less sensitive to prior assumptions and tend to be more precise than in node dating. The total-evidence analysis also shows that four of the seven Hymenoptera calibration points used in node dating are likely to be based on erroneous or doubtful assumptions about the fossil placement. With respect to the early radiation of Hymenoptera, our results suggest that the crown group dates back to the Carboniferous, ∼309 Ma (95% interval: 291--347 Ma), and diversified into major extant lineages much earlier than previously thought, well before the Triassic. [Bayesian inference; fossil dating; morphological evolution; relaxed clock; statistical phylogenetics.].
Evaluating molecular clock calibrations using Bayesian analyses with soft and hard bounds
DOI:10.1098/rsbl.2007.0063 URL [本文引用: 1]
A practical guide to molecular dating
DOI:10.1016/j.crpv.2013.07.003 URL [本文引用: 4]
Testing the impact of calibration on molecular divergence times using a fossil-rich group: The case of Nothofagus (Fagales)
DOI:10.1093/sysbio/syr116
PMID:22201158
[本文引用: 11]

Although temporal calibration is widely recognized as critical for obtaining accurate divergence-time estimates using molecular dating methods, few studies have evaluated the variation resulting from different calibration strategies. Depending on the information available, researchers have often used primary calibrations from the fossil record or secondary calibrations from previous molecular dating studies. In analyses of flowering plants, primary calibration data can be obtained from macro- and mesofossils (e.g., leaves, flowers, and fruits) or microfossils (e.g., pollen). Fossil data can vary substantially in accuracy and precision, presenting a difficult choice when selecting appropriate calibrations. Here, we test the impact of eight plausible calibration scenarios for Nothofagus (Nothofagaceae, Fagales), a plant genus with a particularly rich and well-studied fossil record. To do so, we reviewed the phylogenetic placement and geochronology of 38 fossil taxa of Nothofagus and other Fagales, and we identified minimum age constraints for up to 18 nodes of the phylogeny of Fagales. Molecular dating analyses were conducted for each scenario using maximum likelihood (RAxML + r8s) and Bayesian (BEAST) approaches on sequence data from six regions of the chloroplast and nuclear genomes. Using either ingroup or outgroup constraints, or both, led to similar age estimates, except near strongly influential calibration nodes. Using "early but risky" fossil constraints in addition to "safe but late" constraints, or using assumptions of vicariance instead of fossil constraints, led to older age estimates. In contrast, using secondary calibration points yielded drastically younger age estimates. This empirical study highlights the critical influence of calibration on molecular dating analyses. Even in a best-case situation, with many thoroughly vetted fossils available, substantial uncertainties can remain in the estimates of divergence times. For example, our estimates for the crown group age of Nothofagus varied from 13 to 113 Ma across our full range of calibration scenarios. We suggest that increased background research should be made at all stages of the calibration process to reduce errors wherever possible, from verifying the geochronological data on the fossils to critical reassessment of their phylogenetic position.
Gourds afloat: A dated phylogeny reveals an Asian origin of the gourd family (Cucurbitaceae) and numerous oversea dispersal events
Choosing appropriate substitution models for the phylogenetic analysis of protein-coding sequences
DOI:10.1093/molbev/msj021 URL [本文引用: 2]
Bayesian hypothesis testing of four-taxon topologies using molecular sequence data
The reconstruction of phylogenetic trees from molecular sequences presents unusual problems for statistical inference. For example, three possible alternatives must be considered for four taxa when inferring the correct unrooted tree (referred to as a topology). In our view, classical hypothesis testing is poorly suited to this triangular set of alternative hypotheses. In this article, we develop Bayesian inference to determine the posterior probability that a four-taxon topology is correct given the sequence data and the evolutionary parsimony algorithm for phylogenetic reconstruction. We assess the frequency properties of our models in a large simulation study. Bayesian inference under the principles of evolutionary parsimony is shown to be well calibrated with reasonable discriminating power for a wide range of realistic conditions, including conditions that violate the assumptions of evolutionary parsimony.
Early penguin fossils, plus mitochondrial genomes, calibrate avian evolution
DOI:10.1093/molbev/msj124 URL [本文引用: 1]
An uncorrelated relaxed-clock analysis suggests an earlier origin for flowering plants
Should phylogenetic models be trying to ‘fit an elephant’?
For the past two decades, there has been an ongoing debate within the plylogenetics community over whether model-based approaches for molecular systematics (such as maximum likelihood) should be preferred over the more traditional "maximum parsimony" approach. A recent simulation study by Kolaczkowski and Thornton has brought this debate into sharp focus. In this article, I discuss the significance of their findings and offer a prognosis on the implications for molecular phylogenetics. I believe that biochemistry and model selection have an important role in developing accurate phylogenetic approaches.
Molecular phylogeny of coleoid cephalopods (Mollusca: Cephalopoda) using a multigene approach: The effect of data partitioning on resolving phylogenies in a Bayesian framework
DOI:10.1016/j.ympev.2005.03.020 URL [本文引用: 1]
Bayesian phylogenetic and phylodynamic data integration using BEAST 1.10
Bayesian selection of continuous-time Markov chain evolutionary models
DOI:10.1093/oxfordjournals.molbev.a003872 URL [本文引用: 1]
Bayesian long branch attraction bias and corrections
DOI:10.1093/sysbio/syu099 URL [本文引用: 2]
Some probabilistic and statistical problems in the analysis of DNA sequences
A generation time effect on the rate of molecular evolution in invertebrates
DOI:10.1093/molbev/msq009 URL [本文引用: 1]
Estimating the rate of evolution of the rate of molecular evolution
DOI:10.1093/oxfordjournals.molbev.a025892 URL [本文引用: 1]
A cautionary note on estimating effect size
Complete genomic sequence of human coronavirus OC43: Molecular clock analysis suggests a relatively recent zoonotic coronavirus transmission event
DOI:10.1128/JVI.79.3.1595-1604.2005 URL [本文引用: 1]
The support interval
Puzzling rocks and complicated clocks: How to optimize molecular dating approaches in historical phytogeography
DOI:10.1111/nph.2016.209.issue-4 URL [本文引用: 4]
Testing the molecular clock using mechanistic models of fossil preservation and molecular evolution
Relaxed molecular clocks, the bias-variance trade-off, and the quality of phylogenetic inference
DOI:10.1093/sysbio/syp072
PMID:20525616
[本文引用: 1]

Because a constant rate of DNA sequence evolution cannot be assumed to be ubiquitous, relaxed molecular clock inference models have proven useful when estimating rates and divergence dates. Furthermore, it has been recently suggested that using relaxed molecular clocks may provide superior accuracy and precision in phylogenetic inference compared with traditional time-free methods that do not incorporate a molecular clock. We perform a simulation study to determine if assuming a relaxed molecular clock does indeed improve the quality of phylogenetic inference. We analyze sequence data simulated under various rate distributions using relaxed-clocks, strict-clocks, and time-free Bayesian phylogenetic inference models. Our results indicate that no difference exists in the quality of phylogenetic inference between assuming a relaxed molecular clock and making no assumption about the clock-likeness of sequence evolution. This pattern is likely due to the bias-variance trade-off inherent in this type of phylogenetic inference. We also compared the quality of inference between Bayesian and maximum likelihood time-free inference models and found them to be qualitatively similar.
Green Web or megabiased clock? Plant fossils from Gondwanan Patagonia speak on evolutionary radiations
DOI:10.1111/nph.2015.207.issue-2 URL [本文引用: 1]
Bayesian selection of nucleotide substitution models and their site assignments
DOI:10.1093/molbev/mss258 URL [本文引用: 1]
Improving marginal likelihood estimation for Bayesian phylogenetic model selection
DOI:10.1093/sysbio/syq085 URL [本文引用: 2]
Bayesian phylogenetic inference using DNA sequences: A Markov Chain Monte Carlo Method
DOI:10.1093/oxfordjournals.molbev.a025811 URL [本文引用: 1]
PAML 4: Phylogenetic analysis by maximum likelihood
DOI:10.1093/molbev/msm088 URL [本文引用: 1]
Bayesian estimation of species divergence times under a molecular clock using multiple fossil calibrations with soft bounds
DOI:10.1093/molbev/msj024 URL [本文引用: 3]
Molecular phylogenetics: Principles and practice
DOI:10.1038/nrg3186 URL [本文引用: 4]
Recent progress of sequences analysis methods in molecular evolutionary biology
分子进化生物学中序列分析方法的新进展
Bayesian molecular dating with genomic data
DOI:10.1360/N052018-00224 URL [本文引用: 2]
使用基因组数据进行贝叶斯物种分化时间估计