



生物多样性 ›› 2021, Vol. 29 ›› Issue (4): 456-466. DOI: 10.17520/biods.2020369 cstr: 32101.14.biods.2020369
张剑坛1,2,3, 李艳朋4, 张入匀5, 倪云龙1,2,3, 周文莹1,2,3, 练琚愉1,2,6,*( ), 叶万辉1,2,6
), 叶万辉1,2,6
收稿日期:2020-09-19
接受日期:2020-11-05
出版日期:2021-04-20
发布日期:2021-04-20
通讯作者:
练琚愉
基金资助:
Jiantan Zhang1,2,3, Yanpeng Li4, Ruyun Zhang5, Yunlong Ni1,2,3, Wenying Zhou1,2,3, Juyu Lian1,2,6,*( ), Wanhui Ye1,2,6
), Wanhui Ye1,2,6
Received:2020-09-19
Accepted:2020-11-05
Online:2021-04-20
Published:2021-04-20
Contact:
Juyu Lian
About author:* E-mail: lianjy@scbg.ac.cn摘要:
如何便捷准确地测量树高一直是林学及群落生态学所关心的问题。由于木材密度与树木生长密切相关, 因此基于木材密度建立树高曲线模型能够为测量树高提供新的方法。本文以鼎湖山南亚热带常绿阔叶林1.44 ha塔吊样地内119个物种的4,032个个体为研究对象, 利用树高、胸径和木材密度数据来探究基于枝条木材密度分级的树高曲线模型。首先, 对个体进行随机抽样, 将其划分为建模样本(占总样本量的70%)和检验样本(占总样本量的30%), 并通过聚类分析将所有个体的木材密度划分为4级。其次, 基于建模样本利用常见的5种理论生长方程(Richards、Korf、Logistic、Gompertz和Weibull方程)对不同分级建立树高-胸径模型; 基于检验样本检验模型精度, 并确定各分级的最适模型。最后, 构建基于物种分类的树高曲线模型, 并比较其与木材密度分级模型的差异。结果表明: 基于木材密度分级的模型, 各分级小组检验样本的平均绝对误差(MAE)和均方根误差(RMSE)最小值所对应的模型类型与建模样本结果一致, 确定Gompertz模型和Weibull模型为鼎湖山南亚热带常绿阔叶林最适树高模型类型。比较基于木材密度分级的模型与基于物种分类的模型, 发现二者的MAE、RMSE指数差异小。综上, 基于木材密度分级的树高曲线模型对树高估测精度高, 使用方便, 为树高预测提供了新方法, 可以更好服务森林调查等生产实践。
张剑坛, 李艳朋, 张入匀, 倪云龙, 周文莹, 练琚愉, 叶万辉 (2021) 基于枝条木材密度分级的鼎湖山南亚热带常绿阔叶林树高曲线模型. 生物多样性, 29, 456-466. DOI: 10.17520/biods.2020369.
Jiantan Zhang, Yanpeng Li, Ruyun Zhang, Yunlong Ni, Wenying Zhou, Juyu Lian, Wanhui Ye (2021) Height-diameter models based on branch wood density classification for the south subtropical evergreen broad-leaved forest of Dinghushan. Biodiversity Science, 29, 456-466. DOI: 10.17520/biods.2020369.
| 序号 No. | 模型类型 Model types | 模型表达式 Model forms | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Richards | H = a × (1 - e?b × D)c | ||||||||||
| 2 | Korf | H = a × (e?b/D^c) | ||||||||||
| 3 | Logistic | H = a / (1 + b × e-c × D) | ||||||||||
| 4 | Gompertz | H = a × (e?b × e^(-c × D)) | ||||||||||
| 5 | Weibull | H = a × (1 - e?b × D^c) | ||||||||||
表1 5种候选树高-胸径曲线模型。H为树高; D为胸径; a, b, c为参数。
Table 1 Five kinds of height-diameter models. H, Tree height; D, Diameter at breast height; a, b and c are parameters.
| 序号 No. | 模型类型 Model types | 模型表达式 Model forms | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Richards | H = a × (1 - e?b × D)c | ||||||||||
| 2 | Korf | H = a × (e?b/D^c) | ||||||||||
| 3 | Logistic | H = a / (1 + b × e-c × D) | ||||||||||
| 4 | Gompertz | H = a × (e?b × e^(-c × D)) | ||||||||||
| 5 | Weibull | H = a × (1 - e?b × D^c) | ||||||||||
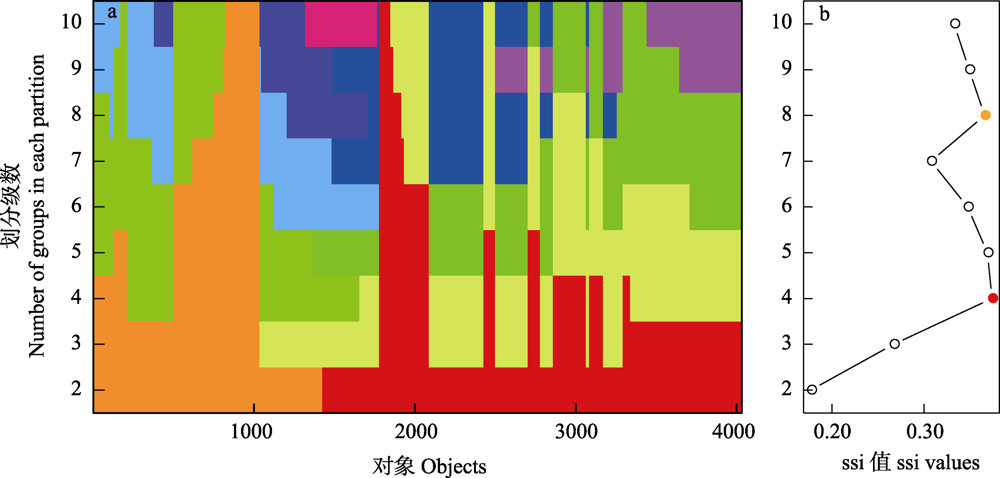
图1 木材密度分级最优分级组数判断指标。(a)表示每个对象在不同分级情况下的归属, 一种颜色代表一个分级组; (b)展示了不同分级组数对应的ssi值大小。
Fig. 1 The judgment index partitioning optimal groups of wood density classification. (a) The groups that each object is categorized with different conditions and different groups were distinguished by different colors; (b) The value of simple structure index (ssi) for different number of groups.
| 组别 Groups | 木材密度范围 Wood density ranges (g/cm3) | 个体数 No. of individuals | 胸径范围 D ranges (cm) | 树高范围 Tree height ranges (m) | 模型表达式 Model expressions |
|---|---|---|---|---|---|
| I | [0.06, 0.31) | 747 | [1.0, 32.8] | [1.5, 21.5] | H = 20.100 × (1 - e?0.111 × D^0.680) |
| II | [0.31, 0.45) | 908 | [1.0, 47.8] | [1.4, 25.7] | H = 54.000 × (1 - e?0.040 × D^0.656) |
| III | [0.45, 0.57) | 1,577 | [1.0, 66.0] | [1.4, 27.1] | H = 20.890 × e?2.257 × e^(-0.098 × D) |
| IV | [0.57, 0.82] | 800 | [1.0, 62.6] | [1.6, 27.1] | H = 51.700 × (1 - e?0.040 × D^0.704) |
表2 基于木材密度分级的树高曲线模型。H为树高, D为胸径。
Table 2 Height-diameter models based on wood density classification. H, Tree height; D, Diameter at breast height.
| 组别 Groups | 木材密度范围 Wood density ranges (g/cm3) | 个体数 No. of individuals | 胸径范围 D ranges (cm) | 树高范围 Tree height ranges (m) | 模型表达式 Model expressions |
|---|---|---|---|---|---|
| I | [0.06, 0.31) | 747 | [1.0, 32.8] | [1.5, 21.5] | H = 20.100 × (1 - e?0.111 × D^0.680) |
| II | [0.31, 0.45) | 908 | [1.0, 47.8] | [1.4, 25.7] | H = 54.000 × (1 - e?0.040 × D^0.656) |
| III | [0.45, 0.57) | 1,577 | [1.0, 66.0] | [1.4, 27.1] | H = 20.890 × e?2.257 × e^(-0.098 × D) |
| IV | [0.57, 0.82] | 800 | [1.0, 62.6] | [1.6, 27.1] | H = 51.700 × (1 - e?0.040 × D^0.704) |
| 组别 Group | 样本数 Sample site | 模型 Model | 参数 Parameter | 拟合精度 Fitting accuracy | 预估精度 Prediction accuracy | 最适模型 Optimal model | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 拟合 Fitting | 检验 Validation | a | b | c | RMSE | AIC | MAE | RMSE | |||
| Ⅰ | 504 | 204 | Richards | 13.300*** | 0.068*** | 0.680*** | 1.070 | 1,503.427 | 0.796 | 1.313 | Weibull |
| Korf | 27.100*** | 2.689*** | 0.349*** | 1.098 | 1,529.476 | 0.821 | 1.338 | ||||
| Logistic | 12.168*** | 4.165*** | 0.232*** | 1.069 | 1,502.340 | 0.844 | 1.334 | ||||
| Gompertz | 13.370*** | 1.841*** | 0.141*** | 1.056 | 1,489.855 | 0.814 | 1.281 | ||||
| Weibull | 20.100*** | 0.111*** | 0.680*** | 1.055 | 1,489.608 | 0.783 | 1.250 | ||||
| II | 637 | 283 | Richards | 34.200*** | 0.013*** | 0.648*** | 1.537 | 2,357.280 | 0.966 | 1.532 | Weibull |
| Korf | 99.700*** | 4.112*** | 0.241*** | 1.621 | 2,430.865 | 1.052 | 1.598 | ||||
| Logistic | 20.517*** | 6.009*** | 0.132*** | 1.575 | 2,394.034 | 1.075 | 1.571 | ||||
| Gompertz | 21.977*** | 2.140*** | 0.078*** | 1.532 | 2,359.453 | 1.013 | 1.529 | ||||
| Weibull | 54.000*** | 0.040*** | 0.656*** | 1.531 | 2,358.118 | 0.960 | 1.520 | ||||
| III | 1,095 | 476 | Richards | 26.816*** | 0.030*** | 0.759*** | 1.753 | 4,344.796 | 1.071 | 1.689 | Gompertz |
| Korf | 163.700*** | 4.627*** | 0.216*** | 1.788 | 4,388.426 | 1.132 | 1.735 | ||||
| Logistic | 19.723*** | 6.575*** | 0.160*** | 1.796 | 4,398.290 | 1.126 | 1.702 | ||||
| Gompertz | 20.890*** | 2.257*** | 0.098*** | 1.746 | 4,335.966 | 1.043 | 1.655 | ||||
| Weibull | 28.980*** | 0.065*** | 0.796*** | 1.758 | 4,350.653 | 1.077 | 1.693 | ||||
| IV | 587 | 243 | Richards | 33.700*** | 0.018*** | 0.697*** | 1.401 | 2,069.142 | 1.030 | 1.639 | Weibull |
| Korf | 83.600*** | 3.979*** | 0.271*** | 1.504 | 2,152.666 | 1.133 | 1.729 | ||||
| Logistic | 21.793*** | 6.432*** | 0.139*** | 1.488 | 2,140.307 | 1.107 | 1.727 | ||||
| Gompertz | 23.945*** | 2.236*** | 0.080*** | 1.422 | 2,087.314 | 1.059 | 1.663 | ||||
| Weibull | 51.700*** | 0.040*** | 0.704*** | 1.394 | 2,063.593 | 1.025 | 1.624 | ||||
表3 不同木材密度分级区间树高曲线模型的拟合与检验。AIC: 赤池信息准则; MAE: 平均绝对误差; RMSE: 均方根误差。 ***, P < 0.001.
Table 3 The fitting and validation results of tree height curve model in different wood density grading ranges. AIC, Akaike information criterion; MAE, Mean absolute error; RMSE, Root mean squared error. ***, P < 0.001.
| 组别 Group | 样本数 Sample site | 模型 Model | 参数 Parameter | 拟合精度 Fitting accuracy | 预估精度 Prediction accuracy | 最适模型 Optimal model | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 拟合 Fitting | 检验 Validation | a | b | c | RMSE | AIC | MAE | RMSE | |||
| Ⅰ | 504 | 204 | Richards | 13.300*** | 0.068*** | 0.680*** | 1.070 | 1,503.427 | 0.796 | 1.313 | Weibull |
| Korf | 27.100*** | 2.689*** | 0.349*** | 1.098 | 1,529.476 | 0.821 | 1.338 | ||||
| Logistic | 12.168*** | 4.165*** | 0.232*** | 1.069 | 1,502.340 | 0.844 | 1.334 | ||||
| Gompertz | 13.370*** | 1.841*** | 0.141*** | 1.056 | 1,489.855 | 0.814 | 1.281 | ||||
| Weibull | 20.100*** | 0.111*** | 0.680*** | 1.055 | 1,489.608 | 0.783 | 1.250 | ||||
| II | 637 | 283 | Richards | 34.200*** | 0.013*** | 0.648*** | 1.537 | 2,357.280 | 0.966 | 1.532 | Weibull |
| Korf | 99.700*** | 4.112*** | 0.241*** | 1.621 | 2,430.865 | 1.052 | 1.598 | ||||
| Logistic | 20.517*** | 6.009*** | 0.132*** | 1.575 | 2,394.034 | 1.075 | 1.571 | ||||
| Gompertz | 21.977*** | 2.140*** | 0.078*** | 1.532 | 2,359.453 | 1.013 | 1.529 | ||||
| Weibull | 54.000*** | 0.040*** | 0.656*** | 1.531 | 2,358.118 | 0.960 | 1.520 | ||||
| III | 1,095 | 476 | Richards | 26.816*** | 0.030*** | 0.759*** | 1.753 | 4,344.796 | 1.071 | 1.689 | Gompertz |
| Korf | 163.700*** | 4.627*** | 0.216*** | 1.788 | 4,388.426 | 1.132 | 1.735 | ||||
| Logistic | 19.723*** | 6.575*** | 0.160*** | 1.796 | 4,398.290 | 1.126 | 1.702 | ||||
| Gompertz | 20.890*** | 2.257*** | 0.098*** | 1.746 | 4,335.966 | 1.043 | 1.655 | ||||
| Weibull | 28.980*** | 0.065*** | 0.796*** | 1.758 | 4,350.653 | 1.077 | 1.693 | ||||
| IV | 587 | 243 | Richards | 33.700*** | 0.018*** | 0.697*** | 1.401 | 2,069.142 | 1.030 | 1.639 | Weibull |
| Korf | 83.600*** | 3.979*** | 0.271*** | 1.504 | 2,152.666 | 1.133 | 1.729 | ||||
| Logistic | 21.793*** | 6.432*** | 0.139*** | 1.488 | 2,140.307 | 1.107 | 1.727 | ||||
| Gompertz | 23.945*** | 2.236*** | 0.080*** | 1.422 | 2,087.314 | 1.059 | 1.663 | ||||
| Weibull | 51.700*** | 0.040*** | 0.704*** | 1.394 | 2,063.593 | 1.025 | 1.624 | ||||
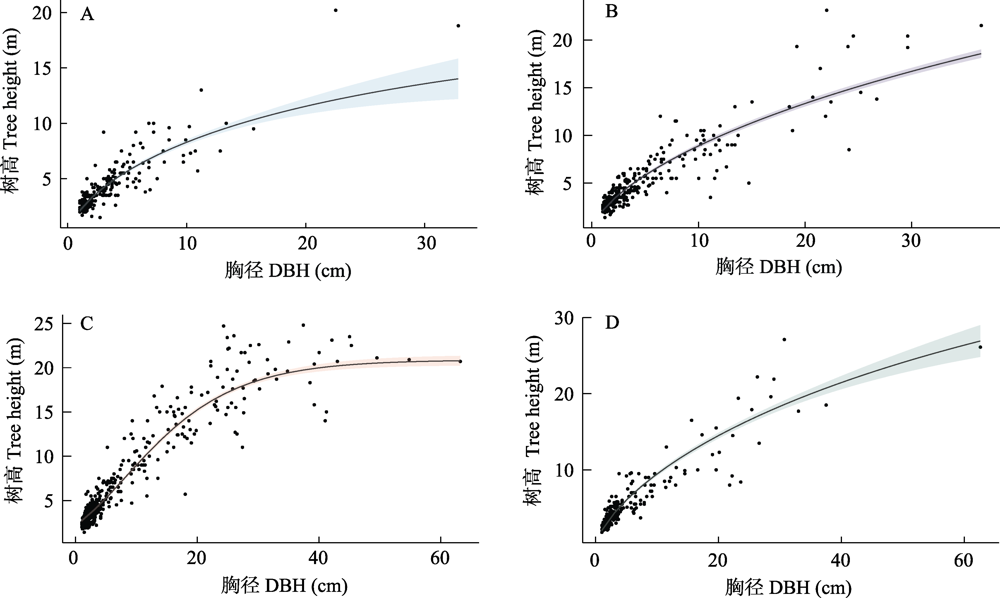
图2 四组木材密度分级区间模型拟合曲线。图A、B、C、D木材密度分别为[0.06, 0.31)、[0.31, 0.45)、[0.45, 0.57)和[0.57, 0.82]。阴影部分为95%置信区间范围。
Fig. 2 Four groups of wood density grading interval model fitting curve and original data distribution diagram. Figure A, B, C and D represent the interval of wood density [0.06, 0.31), [0.31, 0.45), [0.45, 0.57), [0.57, 0.82], respectively. The shaded part represent the 95% confidence interval.
| 物种 Species | 基于物种分类模型 Model based on species classification | 基于木材密度分级模型 Model based on wood density classification | ||||
|---|---|---|---|---|---|---|
| 模型表达式 Model expressions | MAE | RMSE | 模型表达式 Model expressions | MAE | RMSE | |
| 白楸 Mallotus paniculatus | H = 18.621 × e?1.727 × e^(?0.088 × D) | 0.805 | 1.198 | H = 54.000 × (1 - e?0.040 × D^0.656) | 0.961 | 1.323 |
| 橄榄 Canarium album | H = 20.194 × e-2.230 × e^(?0.115 × D) | 0.677 | 0.979 | H = 20.100 × (1 - e?0.111 × D^0.680) | 0.950 | 1.705 |
| 黄杞 Engelhardia roxburghiana | H = 22.881 × (1 - e?0.118 × D^0.774) | 0.678 | 0.992 | H = 54.000 × (1 - e?0.040 × D^0.656) | 1.418 | 1.795 |
| 假苹婆 Sterculia lanceolata | H = 12.486 × e?1.837 × e^(?0.144 × D) | 0.565 | 0.839 | H = 54.000 × (1 - e?0.040 × D^0.656) | 0.611 | 0.960 |
| 九节 Psychotria asiatica | H = 4.063 / (1 + 1.628 × e?0.471 × D) | 0.312 | 0.482 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.848 | 0.927 |
| 黧蒴锥 Castanopsis fissa | H = 9.203 × (1 - e?0.177 × D)0.742 | 0.585 | 0.823 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.934 | 1.567 |
| 罗伞树 Ardisia quinquegona | H = 7.523 / (1 + 4.178 × e?0.637 × D) | 0.454 | 0.593 | H = 51.700 × (1 - e?0.040 × D^0.704) | 0.497 | 0.648 |
| 蒲桃 Syzygium jambos | H = 11.534 / (1 + 4.412 × e?0.242 × D) | 0.718 | 1.030 | H = 51.700 × (1 - e?0.040 × D^0.704) | 1.050 | 1.616 |
| 肉实树 Sarcosperma laurinum | H = 12.527 × e?1.966 × e^(?0.159 × D) | 0.386 | 0.532 | H = 54.000 × (1 - e?0.040 × D^0.656) | 0.460 | 0.678 |
| 水同木 Ficus fistulosa | H = 9.300 × (1 - e?0.204 × D^0.881) | 0.560 | 0.749 | H = 20.100 × (1 - e?0.111 × D^0.680) | 0.674 | 0.873 |
| 鱼骨木 Canthium dicoccum | H = 15.121 × e?2.057 × e^(?0.215 × D) | 1.109 | 1.516 | H = 51.700 × (1 - e?0.040 × D^0.704) | 1.527 | 1.951 |
| 鱼尾葵 Caryota maxima | H = 32.827 / (1 + 8.650 × e?0.090 × D) | 1.881 | 2.563 | H = 54.000 × (1 - e?0.040 × D^0.656) | 2.572 | 3.412 |
| 木荷 Schima superba | H = 20.978 / (1 + 5.011 × e?0.131 × D) | 2.020 | 2.694 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 2.055 | 2.724 |
| 黄果厚壳桂 Cryptocarya concinna | H = 8.149 / (1 + 4.416 × e?0.604 × D) | 0.481 | 0.710 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.691 | 1.066 |
| 鹅掌柴 Schefflera heptaphylla | H = 12.604 × e?1.740 × e^(?0.137 × D) | 0.777 | 1.097 | H = 20.100 × (1 - e?0.111 × D^0.680) | 0.791 | 1.106 |
| 银柴 Aporosa dioica | H = 18.300 × (1 - e?0.107 × D^0.725) | 0.634 | 0.931 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.764 | 1.105 |
| 锥栗 Castanea henryi | H = 19.793 × e?2.253 × e^(?0.101 × D) | 1.662 | 2.247 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 1.752 | 2.346 |
表4 个体数大于50的17个物种基于物种分类模型和木材密度分级模型的差异。H为树高, D为胸径; MAE: 平均绝对误差; RMSE: 均方根误差。
Table 4 Differences between species classification model and wood density classification model of 17 species with more than 50 individuals. H, Tree height, D, Diameter at breast height; MAE, Mean absolute error; RMSE, Root mean squared error.
| 物种 Species | 基于物种分类模型 Model based on species classification | 基于木材密度分级模型 Model based on wood density classification | ||||
|---|---|---|---|---|---|---|
| 模型表达式 Model expressions | MAE | RMSE | 模型表达式 Model expressions | MAE | RMSE | |
| 白楸 Mallotus paniculatus | H = 18.621 × e?1.727 × e^(?0.088 × D) | 0.805 | 1.198 | H = 54.000 × (1 - e?0.040 × D^0.656) | 0.961 | 1.323 |
| 橄榄 Canarium album | H = 20.194 × e-2.230 × e^(?0.115 × D) | 0.677 | 0.979 | H = 20.100 × (1 - e?0.111 × D^0.680) | 0.950 | 1.705 |
| 黄杞 Engelhardia roxburghiana | H = 22.881 × (1 - e?0.118 × D^0.774) | 0.678 | 0.992 | H = 54.000 × (1 - e?0.040 × D^0.656) | 1.418 | 1.795 |
| 假苹婆 Sterculia lanceolata | H = 12.486 × e?1.837 × e^(?0.144 × D) | 0.565 | 0.839 | H = 54.000 × (1 - e?0.040 × D^0.656) | 0.611 | 0.960 |
| 九节 Psychotria asiatica | H = 4.063 / (1 + 1.628 × e?0.471 × D) | 0.312 | 0.482 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.848 | 0.927 |
| 黧蒴锥 Castanopsis fissa | H = 9.203 × (1 - e?0.177 × D)0.742 | 0.585 | 0.823 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.934 | 1.567 |
| 罗伞树 Ardisia quinquegona | H = 7.523 / (1 + 4.178 × e?0.637 × D) | 0.454 | 0.593 | H = 51.700 × (1 - e?0.040 × D^0.704) | 0.497 | 0.648 |
| 蒲桃 Syzygium jambos | H = 11.534 / (1 + 4.412 × e?0.242 × D) | 0.718 | 1.030 | H = 51.700 × (1 - e?0.040 × D^0.704) | 1.050 | 1.616 |
| 肉实树 Sarcosperma laurinum | H = 12.527 × e?1.966 × e^(?0.159 × D) | 0.386 | 0.532 | H = 54.000 × (1 - e?0.040 × D^0.656) | 0.460 | 0.678 |
| 水同木 Ficus fistulosa | H = 9.300 × (1 - e?0.204 × D^0.881) | 0.560 | 0.749 | H = 20.100 × (1 - e?0.111 × D^0.680) | 0.674 | 0.873 |
| 鱼骨木 Canthium dicoccum | H = 15.121 × e?2.057 × e^(?0.215 × D) | 1.109 | 1.516 | H = 51.700 × (1 - e?0.040 × D^0.704) | 1.527 | 1.951 |
| 鱼尾葵 Caryota maxima | H = 32.827 / (1 + 8.650 × e?0.090 × D) | 1.881 | 2.563 | H = 54.000 × (1 - e?0.040 × D^0.656) | 2.572 | 3.412 |
| 木荷 Schima superba | H = 20.978 / (1 + 5.011 × e?0.131 × D) | 2.020 | 2.694 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 2.055 | 2.724 |
| 黄果厚壳桂 Cryptocarya concinna | H = 8.149 / (1 + 4.416 × e?0.604 × D) | 0.481 | 0.710 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.691 | 1.066 |
| 鹅掌柴 Schefflera heptaphylla | H = 12.604 × e?1.740 × e^(?0.137 × D) | 0.777 | 1.097 | H = 20.100 × (1 - e?0.111 × D^0.680) | 0.791 | 1.106 |
| 银柴 Aporosa dioica | H = 18.300 × (1 - e?0.107 × D^0.725) | 0.634 | 0.931 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 0.764 | 1.105 |
| 锥栗 Castanea henryi | H = 19.793 × e?2.253 × e^(?0.101 × D) | 1.662 | 2.247 | H = 20.890 × e?2.257 × e^(?0.098 × D) | 1.752 | 2.346 |
| [1] | Adamec Z, Drápela K (2016) Generalized additive models as an alternative approach to the modelling of the tree height-diameter relationship. Journal of Forest Science, 61,235-243. |
| [2] | Aiba SI, Kohyama T (1996) Tree species stratification in relation to allometry and demography in a warm-temperate rain forest. Journal of Ecology, 84,207-218. |
| [3] |
Bowman DMJS, Brienen RJW, Gloor E, Phillips OL, Prior LD (2013) Detecting trends in tree growth: Not so simple. Trends in Plant Science, 18,11-17.
URL PMID |
| [4] | Cao M, Mo H, Ye JQ (2019) The height growth model of Camellia oleifera based on site type. Forestry and Environmental Science, 35(3),56-62. (in Chinese with English abstract) |
| [ 曹美, 莫辉, 叶嘉齐 (2019) 基于立地类型的油茶树高生长模型. 林业与环境科学, 35(3),56-62. ] | |
| [5] |
Chave J, Coomes D, Jansen S, Lewis SL, Swenson NG, Zanne AE (2009) Towards a worldwide wood economics spectrum. Ecology Letters, 12,351-366.
URL PMID |
| [6] |
Chave J, Muller-Landau HC, Baker TR, Easdale TA, ter Steege H, Webb CO (2006) Regional and phylogenetic variation of wood density across 2456 neotropical tree species. Ecological Applications, 16,2356-2367.
DOI URL PMID |
| [7] | Chen FP, Xu WQ, Yang X, Lu HF (2012) A review of Eucalyptus plantation growth model. World Forestry Research, 25(4),34-38. (in Chinese with English abstract) |
| [ 陈飞鹏, 许文强, 杨雪, 陆宏芳 (2012) 桉树人工林生长模型研究进展. 世界林业研究, 25(4),34-38. ] | |
| [8] | Condit R (1998) Tropical Forest Census Plots: Methods and Results from Barro Colorado Island, Panama and A Comparison with Other Plots. Springer, Berlin. |
| [9] | Cornelissen JHC, Lavorel S, Garnier E, Díaz S, Buchmann N, Gurvich DE, Reich PB, ter Steege H, Morgan HD, van der Heijden MGA, Pausas JG, Poorter H (2003) A handbook of protocols for standardised and easy measurement of plant functional traits worldwide. Australian Journal of Botany, 51,335-380. |
| [10] | Dolnicar S, Grabler K, Mazanec JA (1999) A tale of three cities:Perceptual charting for analyzing destination images. In: Consumer Psychology of Tourism, Hospitality and Leisure (eds Sakai MY, Woodside AG, Crouch GI, Mazanec JA, Oppermann M), pp.39-62. CAB International, New York. |
| [11] | Duan AG, Zhang JG (2013) Research progress of theoretical growth equations. East China Forest Management, 27(1),1-7. (in Chinese with English abstract) |
| [ 段爱国, 张建国 (2013) 理论生长方程研究概述. 华东森林经理, 27(1),1-7. ] | |
| [12] | Feldpausch TR, Banin L, Phillips OL, Baker TR, Lewis SL, Quesada CA, Affum-Baffoe K, Arets EJMM, Berry NJ, Bird M, Brondizio ES, de Camargo P, Chave J, Djagbletey G, Domingues TF, Drescher M, Fearnside PM, França MB, Fyllas NM, Lopez-Gonzalez G, Hladik A, Higuchi N, Hunter MO, Iida Y, Salim KA, Kassim AR, Keller M, Kemp J, King DA, Lovett JC, Marimon BS, Marimon-Junior BH, Lenza E, Marshall AR, Metcalfe DJ, Mitchard ETA, Moran EF, Nelson BW, Nilus R, Nogueira EM, Palace M, Patiño S, Peh KSH, Raventos MT, Reitsma JM, Saiz G, Schrodt F, Sonké B, Taedoumg HE, Tan S, White L, Wöll H, Lloyd J (2011) Height-diameter allometry of tropical forest trees. Biogeosciences, 8,1081-1106. |
| [13] |
Fisher JB, Goldstein G, Jones TJ, Cordell S (2007) Wood vessel diameter is related to elevation and genotype in the Hawaiian tree Metrosideros polymorpha (Myrtaceae). American Journal of Botany, 94,709-715.
DOI URL PMID |
| [14] | Garrard GE, McCarthy MA, Williams NSG, Bekessy SA, Wintle BA (2013) A general model of detectability using species traits. Methods in Ecology and Evolution, 4,45-52. |
| [15] | Gui XJ, Lian JY, Zhang RY, Li YP, Shen H, Ni YL, Ye WH (2019) Vertical structure and its biodiversity in a subtropical evergreen broad-leaved forest at Dinghushan in Guangdong Province, China. Biodiversity Science, 27,619-629. (in Chinese with English abstract) |
| [ 桂旭君, 练琚愉, 张入匀, 李艳朋, 沈浩, 倪云龙, 叶万辉 (2019) 鼎湖山南亚热带常绿阔叶林群落垂直结构及其物种多样性特征. 生物多样性, 27,619-629. ] | |
| [16] | He D (2016) Plant Functional Trait Variation and Community Assembly: A Case Study in a Subtropical Evergreen Forest. PhD dissertation, Sun Yat-Sen University, Guangzhou. (in Chinese with English abstract) |
| [ 何东 (2016) 植物功能性状变异与群落构建: 以黑石顶常绿阔叶林为例. 博士学位论文, 中山大学, 广州. ] | |
| [17] | He P, He DB, Chen ZX, Xiao QH (2020) Compatibility model of stand volume and above-ground biomass based on tree height and crown characteristics. Journal of Central South University of Forestry & Technology, 40(4),28-33. (in Chinese with English abstract) |
| [ 贺鹏, 贺东北, 陈振雄, 肖前辉 (2020) 基于树高和树冠因子的立木材积与地上生物量相容模型研究. 中南林业科技大学学报, 40(4),28-33. ] | |
| [18] | He PC, Ye Q (2019) Plant functional traits: From individual plant to global scale. Journal of Tropical and Subtropical Botany, 27,523-533. (in Chinese with English abstract) |
| [ 贺鹏程, 叶清 (2019) 基于植物功能性状的生态学研究进展: 从个体水平到全球尺度. 热带亚热带植物学报, 27,523-533. ] | |
| [19] | Houghton RA (2005) Aboveground forest biomass and the global carbon balance. Global Change Biology, 11,945-958. |
| [20] | Huang ZL, Kong GH, Wei P (1998) Plant species diversity dynamics in Dinghu Mountain forests. Chinese Biodiversity, 6,116-121. (in Chinese with English abstract) |
| [ 黄忠良, 孔国辉, 魏平 (1998) 鼎湖山植物物种多样性动态. 生物多样性, 6,116-121. ] | |
| [21] | King DA (1996) Allometry and life history of tropical trees. Journal of Tropical Ecology, 12,25-44. |
| [22] | Lei XD, Li XF (2003) A review on growth models of mixed forests. Journal of Beijing Forestry University, 25(3),105-110. (in Chinese with English abstract) |
| [ 雷相东, 李希菲 (2003) 混交林生长模型研究进展. 北京林业大学学报, 25(3),105-110. ] | |
| [23] | Li HK, Fa L (2011) Height-diameter model for major tree species in China using the classified height method. Scientia Silvae Sinicae, 47(10),83-90. (in Chinese with English abstract) |
| [ 李海奎, 法蕾 (2011) 基于分级的全国主要树种树高-胸径曲线模型. 林业科学, 47(10),83-90. ] | |
| [24] | Li J (2019) Classification based height-diameter model for Castanopsis fargesii in Jiangle, Fujian. Journal of Northwest A & F University (Natural Science Edition), 47(11),34-42. (in Chinese with English abstract) |
| [ 李杰 (2019) 基于分级的福建将乐地区栲树树高曲线模型研究. 西北农林科技大学学报(自然科学版), 47(11),34-42. ] | |
| [25] | Li MH, Xiao SZ (2019) Diameter-height models of main tree species in Shanghai. Acta Agriculturae Universitatis Jiangxiensis, 41,501-511. (in Chinese with English abstract) |
| [ 李明华, 肖舜祯 (2019) 上海市主要造林树种的胸径-树高模型研究. 江西农业大学学报, 41,501-511. ] | |
| [26] | Liu FL, Lü Y, Zeng SQ (2011) Status and prospects of forest measurement instruments. Forest Resources Management, (1),96-99. (in Chinese with English abstract) |
| [ 刘发林, 吕勇, 曾思齐 (2011) 森林测树仪器使用现状与研究展望. 林业资源管理, (1),96-99. ] | |
| [27] | Liu RT, Bi RC, Zhao HL (2008) Mathematical simulations of the relationship between height and DBH of Juglans mandshurica population in Taiyue forest region. Journal of Biomathematics, 23,416-422. |
| [28] | Liu WP, Cao HL, Liu W, Lian JY, Wu LF (2011) Study on diversity of monsoon evergreen broad-leaved forest in different kinds of habitat in Dinghushan. Journal of Anhui Agricultural Sciences, 39,16159-16163. [. (in Chinese with English abstract) |
| [ 刘文平, 曹洪麟, 刘卫, 练琚愉, 吴林芳 (2011) 鼎湖山季风常绿阔叶林不同生境物种多样性研究. 安徽农业科学, 39,16159-16163. ] | |
| [29] |
Liu XJ, Ma KP (2015) Plant functional traits—Concepts, applications and future directions. Scientia Sinica Vitae, 45,325-339. (in Chinese with English abstract)
DOI URL |
| [ 刘晓娟, 马克平 (2015) 植物功能性状研究进展. 中国科学: 生命科学, 45,325-339. ] | |
| [30] |
Maharjan SK, Poorter L, Holmgren M, Bongers F, Wieringa JJ, Hawthorne WD (2011) Plant functional traits and the distribution of West African rain forest trees along the rainfall gradient. Biotropica, 43,552-561.
DOI URL |
| [31] |
Martínez-Cabrera HI, Schenk HJ, Cevallos-Ferriz SRS, Jones CS (2011) Integration of vessel traits, wood density, and height in angiosperm shrubs and trees. American Journal of Botany, 98,915-922.
DOI URL PMID |
| [32] |
McGill BJ, Enquist BJ, Weiher E, Westoby M (2006) Rebuilding community ecology from functional traits. Trends in Ecology & Evolution, 21,178-785.
DOI URL PMID |
| [33] | Mehtätalo L (2004) A longitudinal height-diameter model for Norway spruce in Finland. Canadian Journal of Forest Research, 34,131-140. |
| [34] | Meng SX, Huang S, Lieffers VJ, Nunifu T, Yang YQ (2008) Wind speed and crown class influence the height-diameter relationship of lodgepole pine: Nonlinear mixed effects modeling. Forest Ecology and Management, 256,570-577. |
| [35] | Ng’Andwe P, Chungu D, Yambayamba AM, Chilambwe A (2019) Modeling the height-diameter relationship of planted Pinus kesiya in Zambia. Forest Ecology and Management, 447,1-11. |
| [36] | Oksanen J, Blanchet FG, Friendly M, Kindt R, Legendre P, McGlinn D, Minchin PR, O’Hara RB, Simpson GL, Solymos P, Stevens MHH, Szoecs E, Wagner H (2019) vegan: Community Ecology Package. https://CRAN.R-project.org/package=vegan (accessed on 2020-10-27) |
| [37] | Poorter L, McDonald I, Alarcón A, Fichtler E, Licona JC, Peña-Claros M, Sterck F, Villegas Z, Sass-Klaassen U (2010) The importance of wood traits and hydraulic conductance for the performance and life history strategies of 42 rainforest tree species. New Phytologist, 185,481-492. |
| [38] | Poorter L, Rozendaal DMA, Bongers F, de Almeida-Cortez JS, Zambrano AMA, Álvarez FS, Luís Andrade JL, Arreola Villa LF, Balvanera P, Becknell JM, Bentos TV, Bhaskar R, Boukili V, Brancalion PHS, Broadbent EN, César RG, Chave J, Chazdon RL, Dalla Colletta G, Craven D, de Jong BHJ, Denslow JS, Dent DH, DeWalt SJ, Díaz García ED, Manuel Dupuy J, Durán SM, Espírito Santo MM, Fandiño MC, Fernandes GW, Finegan B, Moser VG, Hall JS, Hernández-Stefanoni JL, Jakovac CC, Junqueira AB, Kennard D, Lebrija-Trejos E, Letcher SG, Lohbeck M, Lopez OR, Marín-Spiotta E, Martínez-Ramos M, Martins SV, Massoca PES, Meave JA, Mesquite R, Mora F, Moreno VDS, Müller SC, Muñoz R, Muscarella R, de Oliveira Neto SN, Nunes YRF, Ochoa-Gaona S, Paz H, Peña-Claros M, Piotto D, Ruíz J, Sanaphre-Villanueva L, Sanchez-Azofeifa A, Schwartz NB, Steininger MK, Thomas WW, Toledo M, Uriarte M, Utrera LP, van Breugel M, van der Sande MT, van der Wal H, Veloso MDM, Vester HFM, Vieira ICG, Villa PM, Williamson GB, Wright SJ, Zanini KJ, Zimmerman JK, Westoby M (2019) Wet and dry tropical forests show opposite successional pathways in wood density but converge over time. Nature Ecology & Evolution, 3,928-934. |
| [39] |
Poorter L, Wright SJ, Paz H, Ackerly DD, Condit R, Ibarra-Manríques G, Harms KE, Licona JC, Martínez-Ramos M, Mazer SJ, Muller-Landau HC, Peña-Claros M, Webb CO, Wright IJ (2008) Are functional traits good predictors of demographic rates? Evidence from five Neotropical forests. Ecology, 89,1908-1920.
DOI URL PMID |
| [40] | Richards FJ (1959) A flexible growth function for empirical use. Journal of Experimental Botany, 10,290-301. |
| [41] | Sharma M, Parton J (2007) Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology and Management, 249,187-198. |
| [42] | Shi YL, Wang L, Xia Z (2014) Current progress in the research of allometric scaling and resource limitations models. Science Technology and Engineering, 14(19),159-166. (in Chinese with English abstract) |
| [ 石玉立, 王林, 夏振 (2014) 异速生长和资源限制生物量模型研究的最新进展. 科学技术与工程, 14(19),159-166. ] | |
| [43] |
Swenson NG, Enquist BJ (2008) The relationship between stem and branch wood specific gravity and the ability of each measure to predict leaf area. American Journal of Botany, 95,516-519.
DOI URL PMID |
| [44] | Tang CW, Chen YP, Tao L, Xiao DN (2010) Overview of forest biomass and models of estimating NPP. Arid Zone Research, 27,939-946. (in Chinese with English abstract) |
| [ 汤萃文, 陈银萍, 陶玲, 肖笃宁 (2010) 森林生物量和净生长量测算方法综述. 干旱区研究 , 27,939-946. ] | |
| [45] |
van Gelder HA, Poorter L, Sterck FJ (2006) Wood mechanics, allometry, and life-history variation in a tropical rain forest tree community. New Phytologist, 171,367-378.
DOI URL |
| [46] |
van Leeuwen M, Nieuwenhuis M (2010) Retrieval of forest structural parameters using LiDAR remote sensing. European Journal of Forest Research, 129,749-770.
DOI URL |
| [47] |
Vibrans AC, Moser P, Oliveira LZ, de Maçaneiro JP (2015) Height-diameter models for three subtropical forest types in southern Brazil. Ciência e Agrotecnologia, 39,205-215.
DOI URL |
| [48] | Weiher E, Keddy PA (1995) Assembly rules, null models, and trait dispersion: New questions from old patterns. Oikos, 74,159-164. |
| [49] | Weiss L, Pfestorf H, May F, Körner K, Boch S, Fischer M, Müller J, Prati D, Socher SA, Jeltsch F (2014) Grazing response patterns indicate isolation of semi-natural European grasslands. Oikos, 123,599-612. |
| [50] | Westoby M, Falster DS, Moles AT, Vesk PA, Wright IJ (2002) Plant ecological strategies: Some leading dimensions of variation between species. Annual Review of Ecology and Systematics, 33,125-159. |
| [51] | Wickham H (2016) ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag, New York. |
| [52] | Wright SJ, Kitajima K, Kraft NJB, Reich PB, Wright IJ, Bunker DE, Condit R, Dalling JW, Davies SJ, Díaz S, Engelbrecht BMJ, Harms KE, Hubbell SP, Marks CO, Ruiz-Jaen MC, Salvador CM, Zanne AE (2010) Functional traits and the growth-mortality trade-off in tropical trees. Ecology, 91,3664-3674. |
| [53] | Xu Y, Chen CH, Jiang ZF, Pan HB, Long ML, Cui TQ (2008) Study on correlated models between the diameter at breast height and the tree height of natural red pine. Forest Inventory and Planning, 33(3),56-58. (in Chinese with English abstract) |
| [ 徐悦, 陈昌华, 蒋之富, 潘海波, 龙妙玲, 崔同琦 (2008) 天然赤松胸径与树高相关模型的研究. 林业调查规划, 33(3),56-58. ] | |
| [54] | Yang RC, Kozak A, Smith JHG (1978) The potential of Weibull-type functions as flexible growth curves. Canadian Journal of Forest Research, 8,424-431. |
| [55] | Ye WH, Cao HL, Huang ZL, Lian JY, Wang ZG, Li L, Wei SG, Wang ZM (2008) Community structure of a 20 hm2 lower subtropical evergreen broadleaved forest plot in Dinghushan, China. Journal of Plant Ecology (Chinese Version), 32,274-286. (in Chinese with English abstract) |
| [ 叶万辉, 曹洪麟, 黄忠良, 练琚愉, 王志高, 李林, 魏识广, 王章明 (2008) 鼎湖山南亚热带常绿阔叶林20公顷样地群落特征研究. 植物生态学报, 32,274-286. ] | |
| [56] | Zakharova L, Meyer KM, Seifan M (2019) Trait-based modelling in ecology: A review of two decades of research. Ecological Modelling, 407,108703. |
| [57] | Zhang RY, Li YP, Ni YL, Gui XJ, Lian JY, Ye WH (2019) Intraspecific variation of leaf functional traits along the vertical layer in a subtropical evergreen broad-leaved forest of Dinghushan. Biodiversity Science, 27,1279-1290. (in Chinese with English abstract) |
| [ 张入匀, 李艳朋, 倪云龙, 桂旭君, 练琚愉, 叶万辉 (2019) 鼎湖山南亚热带常绿阔叶林叶功能性状沿群落垂直层次的种内变异. 生物多样性, 27,1279-1290. ] | |
| [58] | Zhang Y, Jia LM (2013) Study advances in growth models of Quercus spp. World Forestry Research, 26(2),48-53. (in Chinese with English abstract) |
| [ 张瑜, 贾黎明 (2013) 栎属树种生长模型研究进展. 世界林业研究, 26(2),48-53. ] | |
| [59] |
Zhao JH, Kang XG, Zhang HD, Liu Y (2009) Relationships between coefficient of variation of diameter and height and competition index of main coniferous trees in Changbai Mountains. Chinese Journal of Applied Ecology, 20,1832-1837. (in Chinese with English abstract)
URL PMID |
|
[ 赵俊卉, 亢新刚, 张慧东, 刘燕 (2009) 长白山主要针叶树种胸径和树高变异系数与竞争因子的关系. 应用生态学报, 20,1832-1837. ]
PMID |
|
| [60] | Zhu YH, Weng GQ (2000) Introduction to tropical rainforest growth and harvest estimation. Forest Resources Management, (6),14-17. (in Chinese) |
| [ 朱永红, 翁国庆 (2000) 热带雨林生长与收获预估简介. 林业资源管理, (6),14-17. ] | |
| [61] | Zhuang CY, Huang QL, Ma ZB, Zheng QR, Wang H (2017) Study on height-diameter relationship in each stratum of typical natural broadleaved forests in mid-subtropics. Forest Research, 30,479-485. (in Chinese with English abstract) |
| [ 庄崇洋, 黄清麟, 马志波, 郑群瑞, 王宏 (2017) 典型中亚热带天然阔叶林各林层树高胸径关系研究. 林业科学研究, 30,479-485. ] |
| [1] | 罗恬, 俞方圆, 练琚愉, 王俊杰, 申健, 吴志峰, 叶万辉. 冠层垂直高度对植物叶片功能性状的影响: 以鼎湖山南亚热带常绿阔叶林为例[J]. 生物多样性, 2022, 30(5): 21414-. |
| [2] | 邵晨, 李耀琪, 罗奥, 王志恒, 席祯翔, 刘建全, 徐晓婷. 不同生活型被子植物功能性状与基因组大小的关系[J]. 生物多样性, 2021, 29(5): 575-585. |
| [3] | 王世彤, 徐耀粘, 杨腾, 魏新增, 江明喜. 微生境对黄梅秤锤树野生种群叶片功能性状的影响[J]. 生物多样性, 2020, 28(3): 277-288. |
| [4] | 曹科, 饶米德, 余建平, 刘晓娟, 米湘成, 陈建华. 古田山木本植物功能性状的系统发育信号及其对群落结构的影响[J]. 生物多样性, 2013, 21(5): 564-571. |
| [5] | 卜文圣, 臧润国, 丁易, 张俊艳, 阮云泽. 海南岛热带低地雨林群落水平植物功能性状与环境因子相关性随演替阶段的变化[J]. 生物多样性, 2013, 21(3): 278-287. |
| [6] | 王国宏, 王小平, 张维康, 李贺, 杜连海, 吴记贵. 北京市自然保护区植物群落对干扰胁迫的抵抗力分析[J]. 生物多样性, 2013, 21(2): 153-162. |
| [7] | 刘建, 李钧敏, 余华, 何维明, 于飞海, 桑卫国, 刘国方, 董鸣. 植物功能性状与外来植物入侵[J]. 生物多样性, 2010, 18(6): 569-576. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
备案号:京ICP备16067583号-7
Copyright © 2022 版权所有 《生物多样性》编辑部
地址: 北京香山南辛村20号, 邮编:100093
电话: 010-62836137, 62836665 E-mail: biodiversity@ibcas.ac.cn