



Biodiv Sci ›› 2011, Vol. 19 ›› Issue (4): 404-413. DOI: 10.3724/SP.J.1003.2011.10020 cstr: 32101.14.SP.J.1003.2011.10020
• Original Papers • Previous Articles Next Articles
Yicheng Wang
Received:2011-01-26
Accepted:2011-05-25
Online:2011-07-20
Published:2011-07-29
Yicheng Wang. A model for designing nature reserves with minimal fragmentation using a primal-dual graph approach[J]. Biodiv Sci, 2011, 19(4): 404-413.
| α | SCP解 SCP solution | r | 模型大小 Model sizea | 目标值 Objective valueb | 时间(秒) Time (s)c | 迭代 Iterationsd | 节点 Nodese |
|---|---|---|---|---|---|---|---|
| 0.8 | 2 | 3 | 0.0 | 3.9 | 11,084 | 61 | |
| 0.7 | 2 | 3 | 0.1 | 10.0 | 34,150 | 238 | |
| 0.6 | 3 | 3 | 952 | 1.6 | 36.2 | 183,910 | 1,810 |
| 0.5 | 3 | 4 | 1,241 | 0.9 | 36.4 | 170,883 | 1,313 |
| 0.4 | 4 | 6 | 200 | 0.1 | 54.6 | 245,866 | 1,308 |
| 0.3 | 5 | 7 | 1.0 | 98.1 | 480,861 | 3,207 | |
| 0.2 | 7 | 9 | 2.8 | 194.0 | 1,056,830 | 8,873 |
Table 1 Computational results of the minimal fragmentation model (No. of sites = 100, No. of species = 30)
| α | SCP解 SCP solution | r | 模型大小 Model sizea | 目标值 Objective valueb | 时间(秒) Time (s)c | 迭代 Iterationsd | 节点 Nodese |
|---|---|---|---|---|---|---|---|
| 0.8 | 2 | 3 | 0.0 | 3.9 | 11,084 | 61 | |
| 0.7 | 2 | 3 | 0.1 | 10.0 | 34,150 | 238 | |
| 0.6 | 3 | 3 | 952 | 1.6 | 36.2 | 183,910 | 1,810 |
| 0.5 | 3 | 4 | 1,241 | 0.9 | 36.4 | 170,883 | 1,313 |
| 0.4 | 4 | 6 | 200 | 0.1 | 54.6 | 245,866 | 1,308 |
| 0.3 | 5 | 7 | 1.0 | 98.1 | 480,861 | 3,207 | |
| 0.2 | 7 | 9 | 2.8 | 194.0 | 1,056,830 | 8,873 |
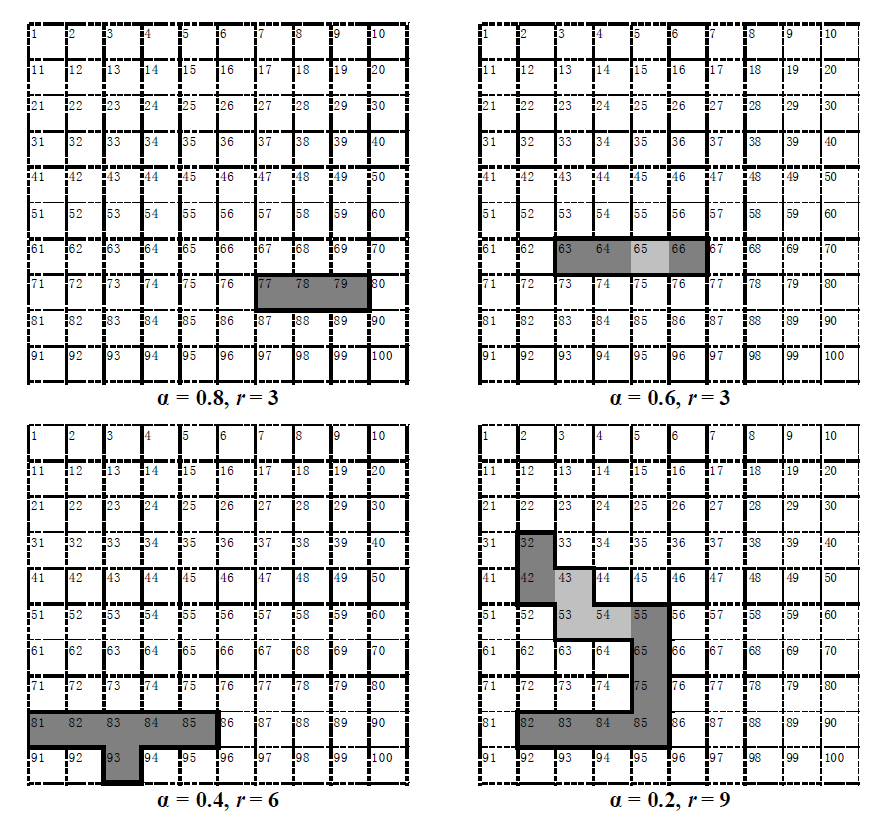
Fig. 5 Selected solutions of the model. Dark grey cells consist of the reserve, shallow grey cells are fragmentation. α, Ratio of species that can coexist in any potential site to total number of species; r, Maximal number of selected sites.
| [1] | Ando A, Camm JD, Polasky S, Solow A (1998) Species distribution, land values and efficient conservation. Science, 279, 2126-2128. |
| [2] | Bolger DT, Scott TA, Rotenberry JT (2001) Use of corridor-like structures by bird and small mammal species. Biological Conservation, 102, 213-224. |
| [3] | Brooke A, Kendrick D, Meeraus A, Raman R (1998) GAMS― A User’s Guide. GAMS Development Corporation, Washington, DC. |
| [4] | Cabeza M, Araújo MB, Wilson RJ, Thomas CD, Cowley MJR, Moilanen A (2004) Combining probabilities of occurrence with spatial reserve design. Journal of Applied Ecology, 41, 252-262. |
| [5] | Church RL, ReVelle C (1974) The maximal covering location problem. Papers of the Regional Science Association, 32, 101-118. |
| [6] | Church RL, Stoms DM, Davis FW (1996) Reserve selection as a maximal covering location problem. Biological Conservation, 76, 105-112. |
| [7] | Cocks KD, Baird IA (1989) Using mathematical programming to address the multiple reserve selection problem: an example from the Eyre Peninsula, South Australia. Biological Conservation, 78, 113-130. |
| [8] | Costello C, Polasky S (2004) Dynamic reserve site selection. Resource and Energy Economics, 26, 157-174. |
| [9] |
Diestel R (2005) Graph Theory, 3rd edn. Springer, Berlin.
URL PMID |
| [10] | Fischer DT, Church RL (2003) Clustering and compactness in reserve site selection: an extension of the biodiversity management area selection model. Forest Science, 49, 555-565. |
| [11] | Fu W (富伟), Liu SL (刘世梁), Cui BS (崔保山), Zhang ZL (张兆苓) (2009) A review on ecological connectivity in landscape ecology. Acta Ecologica Sinica (生态学报), 29, 6174-6182. (in Chinese with English abstract) |
| [12] | Gao ZX (高增祥), Chen S (陈尚), Li DM (李典谟), Xu RM (徐汝梅) (2007) Origin and essence of island biogeography and metapopulation theory. Acta Ecologica Sinica (生态学报), 27, 304-313. (in Chinese with English abstract) |
| [13] | Haight RG, ReVelle CS, Snyder SA (2000) An integer optimization approach to a probabilistic reserve site selection problem. Operations Research, 48, 697-708. |
| [14] | Haight RG, Travis LE (2008) Reserve design to maximize species persistence. Environmental Modeling and Assessment, 13, 243-253. |
| [15] | Hanski I (1998) Metapopulation dynamics. Nature, 396, 41-49. |
| [16] | Harrison P, Spring D, MacKenzie M, Nally RM (2008) Dynamic reserve design with the union-find algorithm. Ecological Modelling, 215, 369-376. |
| [17] | Hodgson JA, Moilanen A, Wintle BA, Thomas CD (2011) Habitat area, quality and connectivity: striking the balance for efficient conservation. Journal of Applied Ecology, 48, 148-152. |
| [18] | Li XW (李晓文), Hu YM (胡远满), Xiao DN (肖笃宁) (1999) Landscape ecology and biodiversity conservation. Acta Ecologica Sinica (生态学报), 19, 399-407. (in Chinese with English abstract) |
| [19] | Nalle DJ, Arthur JL, Sessions J (2002) Designing compact and contiguous reserve networks with a hybrid heuristic algorithm. Forest Science, 48, 59-68. |
| [20] | Önal H (2003) First-best, second-best, and heuristic solutions in conservation reserve selection. Biological Conservation, 115, 55-62. |
| [21] | Önal H, Briers R (2006) Optimum selection of a connected conservation reserve network. Operations Research, 54, 379-388. |
| [22] | Önal H, Wang Y (2008) A graph theory approach for designing conservation reserve networks with minimal fragmentation. Networks, 52, 142-152. |
| [23] | Possingham H, Ball I, Andelman S (2000) Mathematical methods for identifying representative reserve networks. In: Quantitative Methods for Conservation Biology (eds Ferson S, Burgman M), pp. 291-305. Springer, New York. |
| [24] | Tang ZY (唐志尧), Qiao XJ (乔秀娟), Fang JY (方精云) (2009) Species-area relationship in biological communities. Biodiversity Science (生物多样性), 17, 549-559. (in Chinese with English abstract) |
| [25] | Toregas C, Swain R, ReVelle C, Bergman L (1971) The location of emergency service facilities. Operations Research, 19, 1363-1373. |
| [26] | Underhill LG (1994) Optimal and suboptimal reserve selection algorithms. Biological Conservation, 70, 85-87. |
| [27] | Vanegas P, Cattrysse D, Van Orshoven J (2010) Compactness in spatial decision support: a literature review. Lecture Notes in Computer Science, 6016, 414-429. |
| [28] | Williams JC (2002) A zero-one programming model for contiguous land acquisition. Geographical Analysis, 34, 330-349. |
| [29] | Williams JC, ReVelle CS, Levin SA (2004) Using mathematical optimization models to design nature reserves. Frontiers in Ecology and the Environment, 2, 98-105. |
| [30] | Williams JC, ReVelle CS, Levin SA (2005) Spatial attributes and reserve design models: a review. Environmental Modeling and Assessment, 10, 163-181. |
| [31] | Xu HG (徐海根), Wang LL (王连龙), Bao HS (包浩生) (2003) Designing of nature reserve network: a case study of the red-crowned crane nature reserve. Rural Eco-Environment (农村生态环境), 19(4), 5-9. (in Chinese with English abstract) |
| [1] | Jing Gan Xiangxu Liu Xueming Lu Xing Yue. China's Large Cities in Global Biodiversity Hotspots: Conservation Policies and Optimization Directions [J]. Biodiv Sci, 2025, 33(5): 24529-. |
| [2] | Jingjing Zhang, Wenbin Huang, Yiting Chen, Zepeng Yang, Weiye Ke, Zhaojie Peng, Shichao Wei, Zhiwei Zhang, Yisi Hu, Wenhua Yu, Wenliang Zhou. Reef-building coral diversity and distribution characteristics in the National Nature Reserve for Marine Ecology of Guangdong Nanpeng Islands [J]. Biodiv Sci, 2025, 33(4): 24424-. |
| [3] | Guo Yutong, Li Sucui, Wang Zhi, Xie Yan, Yang Xue, Zhou Guangjin, You Chunhe, Zhu Saning, Gao Jixi. Coverage and distribution of national key protected wild species in China’s nature reserves [J]. Biodiv Sci, 2025, 33(3): 24423-. |
| [4] | Lin Wang, Ziyang Yin, Huifang Huang, Jing Wang. A new parameter estimation method based on the Carter-Morley Jones egg- shape model [J]. Biodiv Sci, 2025, 33(1): 24203-. |
| [5] | Tao Qin, Ronghe Cui, Rui Song, Lisha Fu. Chinese public liability insurance for wildlife accidents: Development models, realistic dilemmas, and optimization strategy [J]. Biodiv Sci, 2024, 32(5): 23431-. |
| [6] | Xuemeng Li, Jibao Jiang, Zenglu Zhang, Xiaojing Liu, Yali Wang, Yizhao Wu, Yinsheng Li, Jiangping Qiu, Qi Zhao. Earthworm biodiversity and its influencing factors in Baotianman National Nature Reserve [J]. Biodiv Sci, 2024, 32(4): 23352-. |
| [7] | Qifan Wang, Xiaohui Liu, Ziwei Zhu, Lei Liu, Xinxue Wang, Xuyang Ji, Shaochun Zhou, Zidong Zhang, Hongyu Dong, Minghai Zhang. Mammal and avian diversity in Beijicun National Nature Reserve, Heilongjiang Province, China [J]. Biodiv Sci, 2024, 32(4): 24024-. |
| [8] | Di Suo, Ruoxi Yu, Yuanhui Li, Jiliang Xu. Problem review and optimization path of local legislation in nature reserves in China based on empirical analysis [J]. Biodiv Sci, 2024, 32(2): 23287-. |
| [9] | Xiaolin Liu, Yougui Wu, Minhua Zhang, Xiaorong Chen, Zhicheng Zhu, Dingyun Chen, Shu Dong, Buhang Li, Bingyang Ding, Yu Liu. Community composition and structure of a 25-ha forest dynamics plot of subtropical forest in Baishanzu, Zhejiang Province [J]. Biodiv Sci, 2024, 32(2): 23294-. |
| [10] | Xiaolong Huang, Bingshun Meng, Haibo Li, Wei Ran, Wei Yang, Cheng Wang, Bo Xie, Xu Zhang, Jingcheng Ran, Mingming Zhang. Interspecific associations between Rhinopithecus brelichi and its sympatric species using infrared cameras [J]. Biodiv Sci, 2024, 32(2): 23402-. |
| [11] | Xianglin Yang, Caiyun Zhao, Junsheng Li, Fangfang Chong, Wenjin Li. Invasive plant species lead to a more clustered community phylogenetic structure: An analysis of herbaceous plants in Guangxi’s national nature reserves [J]. Biodiv Sci, 2024, 32(11): 24175-. |
| [12] | Ruirui Mao, Tuo Shen, Hui Li, Linchu Tian, Hairong Tan, Lirong Lu, Xiaogang Wu, Zongji Fan, Guoyi Wu, Jie Li, Yong Wu, Bicheng Zhu, Zhishu Xiao. A dataset of call characteristics of anuran from the Chebaling National Nature Reserve, Guangdong Province [J]. Biodiv Sci, 2024, 32(10): 24356-. |
| [13] | Guofa Cui. Discussion and suggestions on several key issues in the integration and optimization of protected areas [J]. Biodiv Sci, 2023, 31(9): 22447-. |
| [14] | Chao Xing, Yi Lin, Zhiqiang Zhou, Lianjun Zhao, Shiwei Jiang, Zhenzhen Lin, Jiliang Xu, Xiangjiang Zhan. The establishment of terrestrial vertebrate genetic resource bank and species identification based on DNA barcoding in Wanglang National Nature Reserve [J]. Biodiv Sci, 2023, 31(7): 22661-. |
| [15] | Benping Chen, Jianwu Chen, Zhengwen Ling, Xu Yang, Xin Chen, Shengqiang Li, Biao Yang. Developing a dataset on the diversity and dynamic changes of mammals and birds recorded using camera traps in Laojun Mountain National Nature Reserve, Sichuan, China [J]. Biodiv Sci, 2023, 31(5): 22566-. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © 2022 Biodiversity Science
Editorial Office of Biodiversity Science, 20 Nanxincun, Xiangshan, Beijing 100093, China
Tel: 010-62836137, 62836665 E-mail: biodiversity@ibcas.ac.cn ![]()