

|
|
||
|
路径依赖的选择——统一自然选择与中性选择
生物多样性
2024, 32 (7):
24120-.
DOI: 10.17520/biods.2024120
进化思想和方法论并行的、相互独立的自然选择理论和中性选择理论是否能够有效统一起来, 一直是理论生物学重点关注的问题, 而路径依赖的选择提供了一种可能。与中性选择理论一致, 路径依赖的选择也采用了完全对称性的前提假设——自然界的突变完全是基于统计随机性, 不具备方向性, 因而突变没有适合度的差异。但是在一些特定的时空环境下, 环境的正反馈效应导致中性选择对称性的破缺, 促使该突变产生递归效应——拉马克的主动选择或者获得性遗传效应, 这种适宜环境正反馈作用下的生物主动选择与环境自然选择压力下的被动选择产生相互拮抗作用, 并因此在多维的空间条件下形成路径。路径依赖的选择认为生物演化的过程将是一个路径频率的选择过程而不是适合度提高的过程, 并强烈依赖于其历史上所经历的事件或者环境变化等外界条件; 由于不同演化路径之间存在转移概率(比如生物演化中的质粒转移、转座子、生态过程相互作用等), 路径的演化会存在加速或者减速效应, 解释了古尔德等主张的间断平衡论。当环境选择压力很小或者为零的时候, 多数或者所有路径都等价(类似中性选择结果); 而随着环境压力的增大, 不同路径的频率将差异化, 且路径频率比较高的更容易被选择。当环境压力很大, 历史事件等外界因素或者演化过程对路径本身的演化没有影响的时候(静态的、均衡状态), 频率最高的那条路径就是演化所用时间最短或者最优的路径——达尔文自然选择理论的结果。在借鉴了现代物理学, 尤其是量子力学所用的路径积分方法, 路径依赖的选择也许为我们提供了一个不同的视角和方法来解释生物的演化过程。 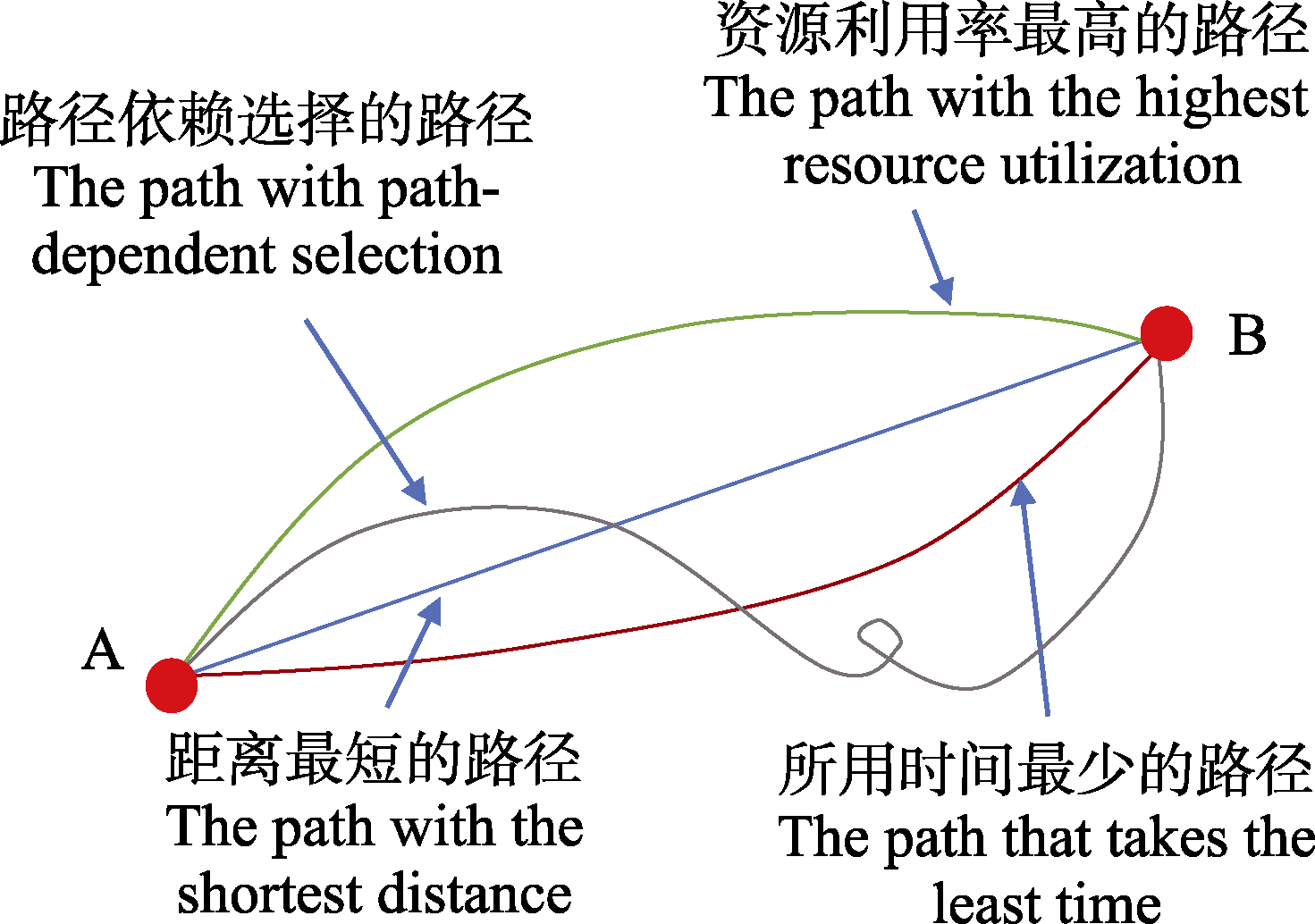 View image in article
图1
不同参数标准下的最优演化路径(改编自Traulsen et al,
正文中引用本图/表的段落
物理学家曾提出这样一个问题: 铅直平面上不在同一铅直线上的两点, 质点在重力的作用下从一个位置运动到另一个位置的可能的运动曲线有无穷多条, 那运动时间最短的一条曲线是哪一条(关洪, 1994)? 物理学将其概括为最速降线问题(Rouse Ball, 1960) (Box 1)。此外, 理论生物学家Arne Traulsen等也根据这个思路, 认为A基因突变到B基因, 在常数适合度下, 只有在选择时间最短的那条路径, 才刚好吻合达尔文自然选择理论(Darwin, 1859; Traulsen et al, 2007)。值得注意的是无论是物理还是生命世界里, 自然演化不一定是选择时间最短的路径演化(Poelwijk et al, 2007; Mustonen & L?ssig, 2010; Steinberg & Ostermeier, 2016; Sohail et al, 2021)。在生物演化中, 这个最优路径可能是时间或距离最短, 也可能是资源利用效率最高, 或是多样性最高, 等等。这样, 根据不同的参数来定义最优路径, 就可能得出不同的最优路径(图1)。
本文的其它图/表
|