最大熵原理(the principle of maximum entropy, 简称MaxEnt或EM)起源于信息科学, 最早由著名数学家、物理学家E. T. Jaynes提出(Jaynes, 1957a, b, 2003), 在信息科学、物理学、天文学、经济学、神经科学等诸多领域有着广泛的应用(Phillips et al., 2006; Banavar et al., 2010), 是统计力学(statistical mechanics)研究的重要内容。我国最早对最大熵原理进行系统介绍的是《最大熵方法》一书(吴乃龙和袁素云, 1991), 后来又出版了《熵气象学》与《组成论》两本专著(张学文和马力, 1992; 张学文, 2003)。
Jaynes最早提出最大熵原理, 是基于Shannon (1948)的信息熵概念。其核心思想是在推断未知概率分布时充分考虑已知信息, 而对未知信息不妄加揣测, 做到不偏不倚。Shannon的信息熵是对信息的一种度量, 信息的增加会导致熵的减少, 从这个意义上说, 在包含已有信息的前提下, 使得熵最大的概率分布是包含未知信息最少的分布, 从而做到“最没有偏见”。
最大熵原理虽然在许多学科中有广泛应用, 但只是近几年才引起生态学家们的关注。用Topic= (("Maximum Entropy" OR MaxEnt OR "Statistical Mechanics") AND (Ecology OR Biodiversity))在ISI Web of Science数据库中进行检索, 可检索到200条记录(
图1
图1
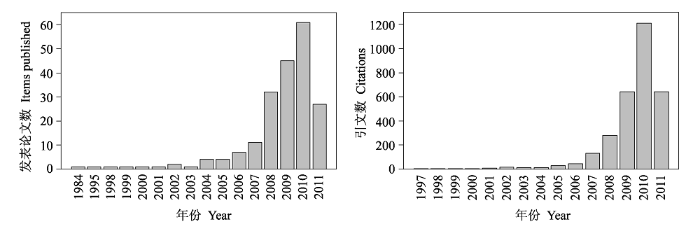
ISI Web of Science数据库检索结果。检索词为Topic=(("Maximum Entropy" OR MaxEnt OR "Statistical Mechanics") AND (Ecology OR Biodiversity)), 检索时间范围为所有年份(检索日期: 2011年5月19日)。左图为各个年份所发表的文章数量, 右图为这些文章的引用情况。
Fig. 1
ISI Web of Science search reports (accessed on 19 May 2011). The searched words are: Topic=(("Maximum Entropy" OR MaxEnt OR "Statistical Mechanics") AND (Ecology OR Biodiversity)). The left one shows items published in each year; the right one shows citations of these papers in each year.
本文中我们先对最大熵原理做简单介绍, 然后对近年来在生态学中的应用及其研究进展进行总结, 以期引起国内同行的关注。
1 最大熵原理概述
通过掷骰子试验可以比较容易地理解最大熵原理(He, 2010; Shipley, 2010b)。将一枚骰子在同一桌面上多次投掷(总投掷次数记为N), 我们只知道N次投掷结果的平均值为μ(假设μ = 5.5), 而对这枚骰子及投掷过程没有更多的信息, 我们想知道的是骰子六个面出现的次数各是多少。
现在假设六个面1, 2, …, 6出现的次数分别为n1, n2, …, n6, 对应的概率为pi = ni/N, 记我们感兴趣的试验结果为向量n = (n1, n2, …, n6)或向量p = (p1, p2, …, p6), 那么这个试验结果对应着很多种可能的“实现”方式。例如取N = 3, 3次投掷的结果是出现两个6点一个2点, 则n = (0, 1, 0, 0, 0, 2), 但这个n对应3种可能的“实现”方式: 2点分别在第一、二、三次投掷中出现。由简单的排列组合知识可知, 向量n对应的实现方式数量为:
我们认为实现方式数量最大的结果就是实际观察到的结果(张学文, 2003), 如果要使向量n最可能出现, 对应的W就应该最大。我们对这个公式简单转换, 两端都取自然对数, 并用Stirling公式取近
似值, 得到:
显然, W最大等价于S最大, 而这个S就是Shannon的信息熵, 于是我们所希望得到的分布应该使得(2)式S取得最大值, 并满足(3)式的约束条件:
(3)式中, xi = i, 这两个式子包含了我们已知的所有信息, 其中第一个式子约束各个面出现的次数加起来等于总投掷次数N, 第二个式子约束N次投掷的平均值为μ。这是一个经典的最优化问题, 可以用Lagrange乘子法来求解, 引入Lagrange乘子λ0和λ1, 整个问题转化为求使得下面(4)式取得最大值的p:
令$\partial \zeta / \partial p_{i}=0$可以求出:
其中,
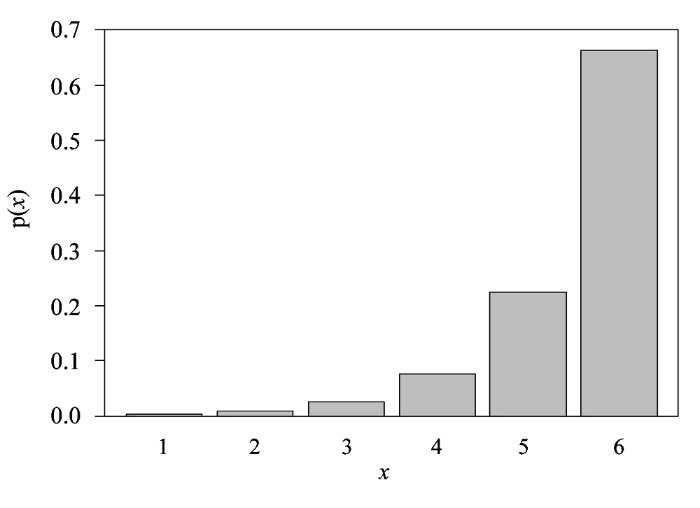
把这个结果带回(3)式即可求出λ0和λ1。在我们的例子中, 取μ = 5.5时可以求出λ0 ≈ 5.932, λ1 ≈ -1.087, 所预测各个面出现的概率如图2所示。这与我们的预期是一致的, 对于一枚均匀骰子的不作弊投掷, 我们的常识是各个面出现的可能性相等, 而多次投掷的结果其平均值应该是(1+2+…+6)/6=3.5; 当现实中出现5.5的平均值时, 我们首先想到的是大点数出现的次数多而小点数出现的次数少, 但在没有任何别的信息的情况下我们只能对骰子的每个面公平对待, 让它们除了满足这个平均值的约束之外尽量等可能地出现, 这就是最大熵原理用有限的已知信息推断未知概率分布的核心思想。事实上, 我们要是取μ = 3.5, 经过简单的计算很容易得到每个面出现的概率是相同的。
图2
图2
均值为5.5的掷骰子试验结果的最大熵估计
Fig. 2
The result of dice throwing predicted by MaxEnt with mean of 5.5
最大熵原理其实是一种贝叶斯推断方法(Shi- pley, 2010b)。在实际应用中, 我们引入p的先验分布p0(Jaynes, 2003; Pueyo et al., 2007), (1)式变为:
相应地需要最大化的熵变为相对熵:
我们前面的例子中先验分布是均匀分布, 也就是认为各个面出现的概率都一样, 所有p0i都相等, 所以简化为(2)式的形式。
现在, 我们对最大熵原理的应用步骤作一简单归纳: 首先要明确研究的问题, 我们要求什么样的概率分布?所“投掷”骰子的各个面分别代表什么?平均值又代表什么?在这些问题都清楚的前提下按照下面的步骤进行求解:
(1)确定所求问题的先验分布, 先验分布应该是包含信息量最小的分布(Pueyo et al., 2007)。
(2)根据实际问题和已知信息确定约束条件((3)式)。
(3)在满足约束条件的同时最大化相对熵((8)式), 求得感兴趣的概率分布。
2 最大熵原理在生态学中的应用
将前面的掷骰子试验换成生态学中不同的实际问题, 最大熵原理就能够简单地应用到生态学当中。张学文(2003)在其专著《组成论》中指出, 任何事物都有一个组成(成分)问题, 即不同的成分在总体中各占多大比重, 而最大熵原理是研究系统组成问题的最佳工具。生态学研究中有很大一部分内容就是研究系统的组成问题的, 比如在群落结构研究中的各物种相对多度问题即是以“物种”作为标签来看整个群落中所有个体的成分, 研究各个物种在整个群落中所占的比重; 再比如同样是群落结构问题的大小分布(size distribution)问题, 所研究的是不同大小(生物量)的个体在群落中的比重; 食物网中的度分布(degree distribution)问题, 研究的是一个食物网的营养链上各物种的食物和天敌种数的分布, 也是典型的组成问题。此外, 还有宏生态学(macroecology)中的许多格局其实也是分布问题, 比如种-面积关系(SAR)、物种多度分布(SAD)等等。事实上这些分布大都是生态学研究的核心问题(Preston, 1948; Hubbell, 2001; Dunne et al., 2002; Brown et al., 2004)。
下面我们就近年来最大熵原理在预测物种相对多度、地理尺度上预测物种空间分布、研究宏生态学格局、推断物种间相互作用、解释食物网的度分布等领域的应用简单总结。
2.1 通过植物性状预测物种相对多度
将前面的掷骰子试验类比为植物群落, 骰子的各个面对应不同的物种, 各个面上的数字对应物种的性状, Shipley等(2006)在法国南部选取处于次生演替不同阶段的一系列废弃葡萄园, 用12块样地的数据研究了30种植物的叶、茎、种子等相关的8个性状与各物种相对多度之间的关系; 用群落水平上各性状的平均值作为约束条件, 运用最大熵原理对各物种在不同群落中的相对多度进行预测, 结果与实测数据有很高的吻合度(R2 = 94%)。他们认为自己的方法避开了种群动态的复杂情况, 实现了用功能性状对植物群落结构的推断, 对传统的“环境过滤”(environmental filtering)概念实现了定量描述(Shipley et al., 2006; Shipley, 2010a)。该研究结果表明, 除了特定的起作用的功能性状之外, 物种可以看作是等价的, 物种间功能性状的差异与群落所处环境完全决定了群落的结构。这里物种间的等价与中性理论完全不同: 在Shipley(2010a, b)的模型中, 物种之间性状上的差异是至关重要的, 而中性理论却是忽略物种之间的性状差异的(Hubbell, 2001)。很多传统生态位理论的追随者也都尝试建立物种相对多度与功能性状、环境之间的联系, 但大都不是很成功, 而忽略物种之间差异的中性理论却能很好地预测物种多度分布, 这一直是中性理论优于生态位理论的有力证据, 而Shipley等人的这项工作改变了这种局面(McGill, 2006)。事实上, Shipley在后续研究中指出, 中性理论可以为最大熵原理提供很好的先验分布(Shipley, 2010b)。
这项工作一经发表就引起生态学家们的极大关注(Marks & Muller-Landau, 2007; Roxburgh & Mokany, 2007; Haegeman & Loreau, 2008, 2009), 也成为最大熵原理在生态学中得到广泛关注的起点。关于这篇文章所引发的争论, 我们将在后文中讨论。
2.2 物种地理分布的生态位模型
物种在地理尺度上的空间分布是生物地理学与保护生物学研究的核心内容。物种空间分布的建模分两种情形: 一种是已知某物种明确的分布区与非分布区, 这种情况下在地理尺度上预测该物种的空间分布比较容易; 另一种情形是只知道某物种出现的一些地区, 而其非分布区并不明确, 这种情况下进行地理尺度上的预测会比较困难。而现实中我们面临更多的是后一种情形。
2006年, S. J. Phillips与同事们合作, 基于生态位理论, 考虑气候、海拔、植被等环境因子, 用最大熵原理作为统计推断工具, 构建了物种地理尺度上空间分布的生态位模型(Phillips et al., 2006; Phi- llips & Dudík, 2008), 并且编写了可以免费获取的软件(
2.3 宏生态学格局的推断
Hubbell中性理论的基本假设是物种之间在生态功能上没有差异(Hubbell, 2001)。尽管很多研究都证实物种间差异的存在是不可否认的(Leigh, 2007), 但中性理论依然能解释生态学中很多问题, 其预测在很多案例中得到了验证, 这在生态位理论支持者看来是不可思议的。Pueyo等(2007)从完全相反的角度出发, 假设每一个种都有自己的特征, 从某种意义上说都是不一样的(ecologically idiosyncratic), 运用最大熵原理推断物种多度分布, 发现中性理论仅仅是大量可能正确的模型之一。
类比前面掷骰子的例子, 在物种多度分布研究中, 骰子的每个面对应于一个多度水平, 而pi对应具有该多度的物种数占总物种数的比例。在Pueyo等的工作中将相对熵(公式(8))最大化, 包含信息量最小的先验分布选为几何级数p0(n) = ψn-1 (Pueyo et al., 2007)。
最近有研究认为(Bowler & Kelly, 2010; Frank, 2011), Pueyo等(2007)对这个分布的解释有欠缺, 但作为先验分布的选择是正确的。有了先验分布, 通过选取不同的约束条件, 就可以得到不同的物种多度分布格局。比如选取归一化条件和群落中每个物种的平均多度为约束条件, 得到的物种多度分布为经典的对数级数分布(Fisher et al., 1943); 在此基础上再加上每个物种多度的几何平均数(实际操作中作对数转换, 化乘积为求和, 还要加入另外一个用作修正的约束)作为约束, 就得到了另一个经典的物种多度分布格局——对数正态分布(Preston, 1948, 1962)。这一结果展示了最大熵原理的强大之处: 十分简洁的假设, 超越了平常的统计模型与机理模型需要简化自然系统复杂性的限制, 所推导的格局与已知的经典分布相符合(Pueyo et al., 2007)。
这项研究与前面提到的Shipley等(2006)的研究正好呈某种程度的互补: Pueyo等(2007)推导的是宏观的物种多度分布格局, 结果为不同多度的物种所占的比重, 而不能得出具体每个物种的相对多度; 而Shipley等(2006)是用物种在功能性状上的差异来推导具体每个物种的相对多度。
Harte等(2008)从状态变量(state-variable)的概念出发, 参考热力学中的理想气体模型将最大熵原理应用于生态学中, 来推断宏生态学格局, 如物种多度分布、种-面积关系、特有种-面积关系(EAR)、多度-能量关系(AER)等。其中, 选取的4个“状态变量”分别为: 群落面积A0、总物种数S0、总个体数N0以及总代谢率E0。在用最大熵原理求解这些格局的时候并没有考虑任何机理, 就像热力学中一样, 仅仅用这些状态变量作为约束条件来得到对这些格局的预测。运用最大熵原理很自然地推导出了Fisher的物种多度分布对数级数分布; 种-面积关系在双对数坐标系中呈负曲率, 但是随着物种数与个体数比值的下降, 越来越接近于斜率介于0.14-0.20之间的幂率分布。这些结果同时得到了观测数据的强力支持, 预测结果与已有的普查数据(CTFS系统BCI、Cocoli、Sherman等大样地的数据)(Harte et al., 2008;
Dewar和Porte(2008)运用最大化相对熵的方法, 通过建立简单的资源利用模型, 推导了局域尺度上多样性-生产力关系、物种多度分布(对数正态)等生态格局, 并利用前人发表的数据对所作的预测进行了验证, 使最大化相对熵的预测结果得到了数据的支持。他们强调, 这些生态格局与热力学系统的表现之间存在数学相似性, 提出生态格局的解释不应该只局限于生态学, 它可能还反映了高自由度的复杂系统在一些非常宏观的环境约束之下所显示的相似的统计格局。
2.4 物种间相互作用的推断
Volkov等(2009)提出两种互补的方法来推断群落中物种间的有效相互作用力(the effective interaction strength): 第一种基于最大熵原理, 第二种是随机生-死模型(stochastic birth-death model), 两种方法所得到的结果高度一致。他们的研究结果表明在巴拿马BCI森林大样地中, 与种内作用相比, 种间相互作用是很弱的(比种内作用小一个数量级), 这为忽略物种间相互作用的中性理论能够很好地预测BCI许多静态和动态格局提供了一种解释。在这项研究中, 作者将整个大样地划分成许多同样大小的栅格, 每个物种在每个栅格中有一个多度, 一个栅格中所有研究物种的多度构成一个多度向量n = (n1, n2, …, nS), 而这个向量就和我们掷骰子例子中的骰子的面对应起来, 不同的是每个面不仅仅对应一个点数, 而是对应一个向量, 所要探究的分布不再是一元的p(xi), 而是多元的p(n)。作者用归一化条件和各物种在一个栅格中的平均多度以及两两物种对多度的乘积在一个栅格中的均值作为约束条件, 用最大熵原理来推断分布p(n)。在这个推断过程中, 物种间有效相互作用是一个涌现(emergent)的结果(Volkov et al., 2009)。
值得注意的是, 另一项与Volkov等(2009)类似的工作即Azaele等(2010)的工作几乎同时发表。只是后者所采用的数据集不同, 他们没有详细的物种多度数据, 而是仅用物种出现与否(presence/abs- ence)的数据来研究了生态系统的结构, 同样得到了物种之间相互作用的网络(Azaele et al., 2010)。
2.5 食物网的度分布
度分布是复杂网络研究中的重要概念(Strogatz, 2001; 王林和戴冠中, 2006), 在食物网结构建模中扮演着重要角色(Williams, 2010)。在食物网中, 度分布是指其营养链上不同物种的食物和天敌种数的分布。尽管度分布在复杂网络的描述中占有十分重要的地位, 其研究也十分广泛(Strogatz, 2001; 王林和戴冠中, 2006), 然而对于度分布的机理或者统计学上的解释却很少。Williams(2010)运用最大熵原理构建的简单模型能够对食物网度分布进行很好的预测, 这为度分布背后的机理提供了一种解释, 即虽然食物网的结构受很多生态过程的影响, 但是其度分布却是独立于这些生态过程的。Williams (2010)对最大熵原理的使用和我们前面掷骰子的例子很接近, 骰子中各个面对应食物网中的物种, 各个面的点数对应该物种的食物(天敌)种数, 约束条件包括归一化条件和每个物种在该食物网中食物(天敌)种数的平均值。在食物网之外, Williams (2011)还用同样的方法研究了植物—传粉者、植物-种子传播者以及植物-植食动物等二分网络(bipartite networks)中的度分布, 得到了很好的预测效果。
3 争论与进展
由于逻辑上的简洁以及在实际应用中的良好表现, 近年来最大熵原理在生态学中得到了极大的关注。但是生态系统毕竟不同于物理系统, 从统计物理中借鉴过来的最大熵原理在生态学中能占据什么样的地位, 以及其对生态学分布预测的可靠性究竟有多高也引起了广泛的争论。
目前这些争论主要围绕Shipley等(2006)的工作展开。Roxburgh和Mokany(2007)认为Shipley等(2006)对最大熵原理的应用在数学上存在不独立性, 他们使用的群落水平上的性状平均值是由实际观测到的物种相对多度计算的, 而后面又用这些平均性状作为最大熵的约束条件来预测物种相对多度, 属于循环论证。Marks和Muller-Landau(2007)也指出了这个问题, 另外他们用交叉验证(cross-validation)的方法对Shipley等(2006)的工作做了检验, 发现在交叉验证中最大熵模型的预测能力要大大低于原工作中所报道的94%。Haegeman和Loreau(2008, 2009)认为Shipley等(2006)研究中好的结果来源于他们很好的数据集以及太过严格的约束条件, 事实上不能为最大熵原理在生态学中的应用提供任何支持。Haegeman和Loreau(2008, 2009)通过对比生态学与物理学中最大熵原理的不同表现, 指出最大熵原理在物理学中的成功源于物理系统高的自由度, 而生态学的尴尬在于其自由度不够大(Haegeman & Loreau, 2008), 所以想要在生态学中成功运用最大熵原理并不是一件容易的事情。
针对这些批评, Shipley都一一作出了回应(Shi- pley et al., 2007; Shipley, 2009a, b)。事实上,单从模型的角度讲, 循环论证的指责是不对的, 虽然人们期望一个模型的参数能够独立于其所拟合的数据, 但现实中很少有模型能满足这个条件, 就拿最常使用的线性回归来说, 其参数也需要先用数据进行拟合, 所以这是一个自由度的问题, 不能简单地定义为循环论证(McGill & Nekola, 2010; Shipley, 2010b)。就数据获取的角度而言, 群落平均性状还可由别的方法如从遥感数据得到(He, 2010), 而Shipley等(2006)工作的出发点是由环境来预测群落平均性状, 进而得到环境对群落结构的预测(Shipley, 2010b), 故而循环论证不应该成为批评最大熵模型的理由。对一个模型预测能力的最终判定需要依靠强有力的统计检验以及实证数据的支持, 这方面的研究已经有所进展, 比如Shipley(2010c)本人就发展了一种置换检验(permutation test)方法, 并对Shipley等(2006)和Pueyo等(2007)的工作进行了检验。Roxburgh和Mokany (2010)也在他们前期工作的基础上发展了相应的统计检验方法。最近, Shipley和合作者也用实证数据对他们的模型做了有力的检验(Sonnier et al., 2010; Shipley et al., 2011)。Merow等(2011)通过对最大熵模型预测力与局限性的系统研究, 发现在不同多样性水平、不同优势度水平的群落中, 最大熵模型都能很好地预测对群落平均性状起决定作用的主要物种的相对多度, 其预测结果都好于无效模型(null models)与回归模型。Merow等(2011)还指出, 最大熵模型对性状的选择敏感, 使用基于无效模型的先验分布可以大幅提高其预测力。
这些争论也引起了其他生态学家的兴趣, Oikos杂志2010年第4期刊出了4篇相关的专题文章来探讨最大熵原理在生态学中的应用, 分别是: 最大熵原理与大家所熟知的统计方法(如Logistic回归)之间联系的探讨(He, 2010)、从实用主义角度对最大熵原理的评价(McGill & Nekola, 2010)、对最大熵模型预测结果的统计检验方法的探讨(Roxburgh & Mokany, 2010), 以及Shipley(2010a, b)本人对其模型背后的生态机理的探讨。
最大熵原理在生态学中的应用也引起了物理学家的注意(Banavar et al., 2010; Bowler & Kelly, 2010)。在Pueyo等(2007)工作的基础上, Bowler和Kelly(2010)通过运用最大熵原理研究物种多度分布, 找到了物种多度分布背后的生态机理, 构建了一个涵盖从中性理论到极端的生态位理论(Pueyo et al., 2007)所有生态模型的SAD分布框架, 成功地实现了生态位理论与中性理论的融合。该研究表明, 物种多度分布主要由两类基本生态学参数决定, 一个是群落中所有物种总个体数, 另一个是单位出生率和死亡率(per capita birth rates and death rates), 其他的一些约束如单个物种的多度和物种间的相关性在决定SAD格局中所起作用不大。
最大熵原理在生态学中的应用也推进了生态学的发展。如Volkov等(2009)和Azaele等(2010)提供了将物种间相互作用加入到生态系统结构与动态研究中的途径, Williams(2010)为食物网的度分布提供了机理解释, 物种地理分布的最大熵模型还为生物地理学与保护生物学提供了有力的预测工具(Phillips et al., 2006), 最大熵原理对宏生态学格局的推断也推进了生态学中统一格局与统一理论的研究(Frank, 2009, 2011; Bowler & Kelly, 2010; McGill, 2010)。
4 结语
综上所述,最大熵原理为生态学的发展注入了新的活力。但这些研究还刚刚起步, 还存在很多争论, 许多问题还有待进一步研究。我们这里要强调的是源于信息论与统计物理的最大熵原理本身仅仅是一种用有限信息来客观地推断未知概率分布的方法, 并不能代替真正的生态学研究。最大熵原理的应用有很多问题需要注意, 比如先验分布的选择、约束条件的设置等等, 这些步骤对最大熵原理的应用至关重要(Pueyo et al., 2007; Banavar et al., 2010; Haegeman & Etienne, 2010)。只有对所研究的生态问题有清楚的认识与表达, 我们才可能正确地运用最大熵原理。生态学家对自然界中统一格局的向往、对统一方法与理论的追求, 都是生态科学发展的动力。对最大熵原理更广泛的讨论与应用可能会给生态学带来新的发展。
参考文献
Inferring plant ecosystem organization from species occurrences
Applications of the principle of maximum entropy: from physics to ecology
The general theory of species abundance distributions
Toward a metabolic theory of ecology
Statistical mechanics unifies different ecological patterns
Food-web structure and network theory: the role of connectance and size
A statistical explanation of MaxEnt for ecologists
The relation between the number of species and the number of individuals in a random sample of an animal population
The common patterns of nature
DOI:10.1111/j.1420-9101.2009.01775.x
URL
PMID:19538344
[本文引用: 1]

We typically observe large-scale outcomes that arise from the interactions of many hidden, small-scale processes. Examples include age of disease onset, rates of amino acid substitutions and composition of ecological communities. The macroscopic patterns in each problem often vary around a characteristic shape that can be generated by neutral processes. A neutral generative model assumes that each microscopic process follows unbiased or random stochastic fluctuations: random connections of network nodes; amino acid substitutions with no effect on fitness; species that arise or disappear from communities randomly. These neutral generative models often match common patterns of nature. In this paper, I present the theoretical background by which we can understand why these neutral generative models are so successful. I show where the classic patterns come from, such as the Poisson pattern, the normal or Gaussian pattern and many others. Each classic pattern was often discovered by a simple neutral generative model. The neutral patterns share a special characteristic: they describe the patterns of nature that follow from simple constraints on information. For example, any aggregation of processes that preserves information only about the mean and variance attracts to the Gaussian pattern; any aggregation that preserves information only about the mean attracts to the exponential pattern; any aggregation that preserves information only about the geometric mean attracts to the power law pattern. I present a simple and consistent informational framework of the common patterns of nature based on the method of maximum entropy. This framework shows that each neutral generative model is a special case that helps to discover a particular set of informational constraints; those informational constraints define a much wider domain of non-neutral generative processes that attract to the same neutral pattern.
Measurement scale in maximum entropy models of species abundance
Entropy maximization and the spatial distribution of species
Limitations of entropy maximization in ecology
Trivial and non-trivial applications of entropy maximization in ecology: a reply to Shipley
Maximum entropy and the state-variable approach to macroecology
Maximum entropy, logistic regression, and species abundance
Information theory and statistical mechanics
Information theory and statistical mechanics. II
Neutral theory: a historical perspective
Maximum entropy niche-based modeling (MaxEnt) of potential geographical distributions of fruit flies Dacus bivittatus, D. ciliatus and D. vertebrates (Diptera: Tephritidae)
Modeling potential habitat for alien species of Dreissena polymorpha in the Continental USA
Comment on “From Plant Traits to Plant Communities: A Statistical Mechanistic Approach to Biodiversity”
A renaissance in the study of abundance
Towards a unification of unified theories of biodiversity
DOI:10.1111/j.1461-0248.2010.01449.x
URL
PMID:20337695
[本文引用: 1]

A unified theory in science is a theory that shows a common underlying set of rules that regulate processes previously thought to be distinct. Unified theories have been important in physics including the unification of electricity and magnetism and the unification of the electromagnetic with the weak nuclear force. Surprisingly, ecology, specifically the subfields of biodiversity and macroecology, also possess not one but at least six unified theories. This is problematic as only one unified theory is desirable. Superficially, the six unified theories seem very different. However, I show that all six theories use the same three rules or assertions to describe a stochastic geometry of biodiversity. The three rules are: (1) intraspecifically individuals are clumped together; (2) interspecifically global or regional abundance varies according to a hollow curve distribution; and (3) interspecifically individuals are placed without regard to individuals of other species. These three rules appear sufficient to explain local species abundance distributions, species-area relationships, decay of similarity of distance and possibly other patterns of biodiversity. This provides a unification of the unified theories. I explore implications of this unified theory for future research.
Mechanisms in macroecology: AWOL or purloined letter? Towards a pragmatic view of mechanism
DOI:10.1111/j.1600-0706.2009.17771.x URL [本文引用: 2]
Can entropy max- imization use functional traits to explain species abund- ances? A comprehensive evaluation
Maximum entropy modeling of species geographic distributions
Modeling of species distributions with MaxEnt: new extensions and a comprehensive evaluation
The canonical distribution of commonness and rarity: Part I
The maximum entropy formalism and the idiosyncratic theory of biodiversity
DOI:10.1111/j.1461-0248.2007.01096.x
URL
PMID:17692099
[本文引用: 12]

Why does the neutral theory, which is based on unrealistic assumptions, predict diversity patterns so accurately? Answering questions like this requires a radical change in the way we tackle them. The large number of degrees of freedom of ecosystems pose a fundamental obstacle to mechanistic modelling. However, there are tools of statistical physics, such as the maximum entropy formalism (MaxEnt), that allow transcending particular models to simultaneously work with immense families of models with different rules and parameters, sharing only well-established features. We applied MaxEnt allowing species to be ecologically idiosyncratic, instead of constraining them to be equivalent as the neutral theory does. The answer we found is that neutral models are just a subset of the majority of plausible models that lead to the same patterns. Small variations in these patterns naturally lead to the main classical species abundance distributions, which are thus unified in a single framework.
Comment on “From Plant Traits to Plant Communities: A Statistical Mechanistic Approach to Biodiversity”
On testing predictions of species relative abundance from maximum entropy optimisation
DOI:10.1111/j.1600-0706.2009.17772.x URL [本文引用: 2]
A mathematical theory of communication
Limitations of entropy maximization in ecology: a reply to Haegeman and Loreau
Trivial and non-trivial applications of entropy maximization in ecology: Shipley’s reply
Community assembly, natural selection and maximum entropy models
DOI:10.1111/j.1600-0706.2009.17770.x URL [本文引用: 3]
Inferential permutation tests for maximum entropy models in ecology
A strong test of maximum entropy model of trait-based community assembly
DOI:10.1890/10-0394.1
URL
PMID:21618929
[本文引用: 1]

From plant traits to plant communities: a statistical mechanistic approach to biodiv- ersity
DOI:10.1126/science.1131344
URL
PMID:17023613
[本文引用: 11]

We developed a quantitative method, analogous to those used in statistical mechanics, to predict how biodiversity will vary across environments, which plant species from a species pool will be found in which relative abundances in a given environment, and which plant traits determine community assembly. This provides a scaling from plant traits to ecological communities while bypassing the complications of population dynamics. Our method treats community development as a sorting process involving species that are ecologically equivalent except with respect to particular functional traits, which leads to a constrained random assembly of species; the relative abundance of each species adheres to a general exponential distribution as a function of its traits. Using data for eight functional traits of 30 herbaceous species and community-aggregated values of these traits in 12 sites along a 42-year chronosequence of secondary succession, we predicted 94% of the variance in the relative abundances.
Response to Comments on “From Plant Traits to Plant Communities: A Statistical Mec- hanistic Approach to Biodiversity”
Plant traits, species pools and the prediction of relative abundance in plant communities: a maximum entropy approach
Exploring complex networks
DOI:10.1038/35065725
URL
PMID:11258382
[本文引用: 2]

The study of networks pervades all of science, from neurobiology to statistical physics. The most basic issues are structural: how does one characterize the wiring diagram of a food web or the Internet or the metabolic network of the bacterium Escherichia coli? Are there any unifying principles underlying their topology? From the perspective of nonlinear dynamics, we would also like to understand how an enormous network of interacting dynamical systems-be they neurons, power stations or lasers-will behave collectively, given their individual dynamics and coupling architecture. Researchers are only now beginning to unravel the structure and dynamics of complex networks.
Inferring species interactions in tropical forests
On degree distribution of complex network
Application of ROC curve analysis in evaluating the performance of alien species' potential distribution models
Simple MaxEnt models explain food web degree distributions
Biology, methodology or chance? The degree distributions of bipartite ecological networks
DOI:10.1371/journal.pone.0017645
URL
PMID:21390231
[本文引用: 1]

The distribution of the number of links per species, or degree distribution, is widely used as a summary of the topology of complex networks. Degree distributions have been studied in a range of ecological networks, including both mutualistic bipartite networks of plants and pollinators or seed dispersers and antagonistic bipartite networks of plants and their consumers. The shape of a degree distribution, for example whether it follows an exponential or power-law form, is typically taken to be indicative of the processes structuring the network. The skewed degree distributions of bipartite mutualistic and antagonistic networks are usually assumed to show that ecological or co-evolutionary processes constrain the relative numbers of specialists and generalists in the network. I show that a simple null model based on the principle of maximum entropy cannot be rejected as a model for the degree distributions in most of the 115 bipartite ecological networks tested here. The model requires knowledge of the number of nodes and links in the network, but needs no other ecological information. The model cannot be rejected for 159 (69%) of the 230 degree distributions of the 115 networks tested. It performed equally well on the plant and animal degree distributions, and cannot be rejected for 81 (70%) of the 115 plant distributions and 78 (68%) of the animal distributions. There are consistent differences between the degree distributions of mutualistic and antagonistic networks, suggesting that different processes are constraining these two classes of networks. Fit to the MaxEnt null model is consistently poor among the largest mutualistic networks. Potential ecological and methodological explanations for deviations from the model suggest that spatial and temporal heterogeneity are important drivers of the structure of these large networks.
Prediction of potential geographic distribution of Microcyclus ulei in the world using MaxEnt