

|
|
||
|
样本量不一致时的β多样性计算
生物多样性
2021, 29 (6):
790-797.
DOI: 10.17520/biods.2021011
度量样方间物种组成的差异, 即β多样性, 是生态学研究中的常用手段。在开展生态学研究的过程中, 不同样方获取的样本量通常不同。使用物种稀疏曲线可以计算不同样本量的α多样性, 但常用的β多样性指数的计算却没有考虑样本量的差异。本文主要介绍了从稀疏曲线演化而来的可以计算不同样本量的β多样性指数——预期共享物种数(expected species shared, ESS)及其标准化后的指数, 其中详细介绍了弦标准化的预期共享物种数(chord-normalized expected species shared, CNESS)。利用真实采集的数据集, 本文演示了在不同样本参数m下, CNESS经过主坐标分析(principal coordinates analysis, PCoA)的二维排序结果, 并比较了样本量变化后, CNESS与基于多度的Chao-Jaccard相异性指数之间的差异。模拟结果表明, CNESS指数与Chao-Jaccard指数的PCoA结果具有相关性, 该相关性不随m值的变化而变化。CNESS指数较Chao-Jaccard指数具有更多优势, 通过调节样本参数m, CNESS的结果可以分析优势种或者稀有种的物种组成差异, 同时CNESS指数对样本量不敏感。ESS系列相异指数是基于物种多度的计算, 适用于样本量不一致时的β多样性研究, 建议在开展昆虫等无脊椎动物的生态学研究中使用此指数。为了更加准确地获得样方之间的物种组成差异, 在数据分析的过程中应选取不同大小的m值计算CNESS。然而, 由于样本量小于特定m值的样方会在计算中被剔除, 因此, 在实际的取样工作中, 每个样方都应该尽量采集到足够多的个体, 才能保证在m值足够大的时候也不丢失样方信息。 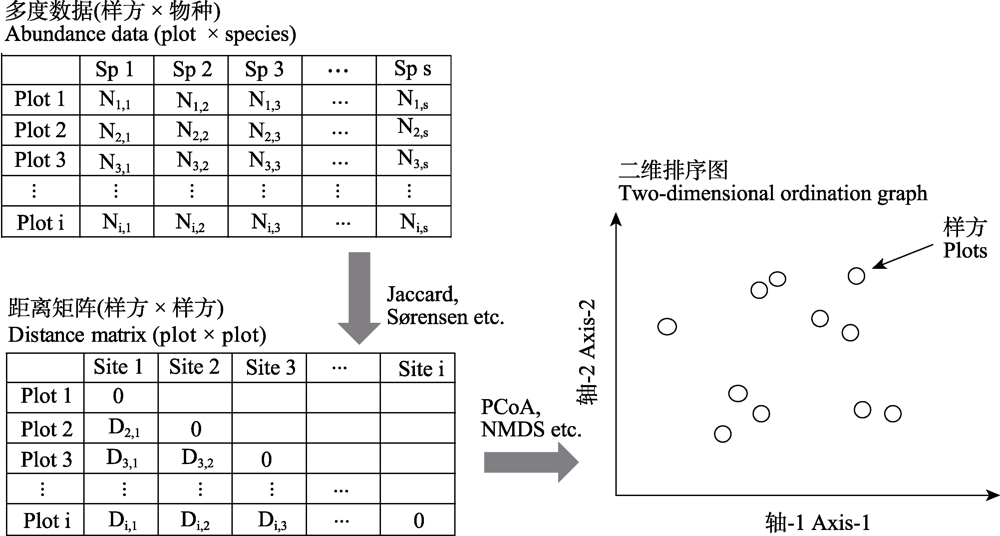 View image in article
图1
从样方 × 物种的多度数据转换成二维排序图的流程图。原始的多度数据通过计算相异指数可以得到一个两两样方配对的距离矩阵; 该距离矩阵可以通过合适的排序方法得到二维的降序图; 二维图中的一个点代表一个样方, 点与点之间的距离代表样方之间的物种组成是相异(距离比较远)还是相似(距离比较近)。
正文中引用本图/表的段落
β多样性的算法大致可以分为两类: 一类是与γ多样性相关的倍性(γ/α)或加性(γ - α)分配法, 另一类是测量样方之间的相似性或相异性。度量样方之间的相似性(或相异性)被广泛用于测定时间或者空间维度上群落组成的变化(陈圣宾等,2010; 斯幸峰等, 2017), 其计算结果通常是获得一个样方 × 样方的距离矩阵(dissimilarity/distance matrix)。基于物种频度分布的β多样性指数有Jaccard指数、S?rensen指数、Cody指数、Whittaker指数等(Koleff et al, 2003); 基于物种多度的β多样性指数包括改进后的Jaccard与S?rensen指数(这里分别称为Chao-Jaccard指数和Chao-S?rensen指数)、Bray-Curtis指数(Chaoet al, 2005; Schroeder & Jenkins, 2018), 或者直接采用物种多度的欧式距离(Euclidean distance)等(Legendre & Legendre, 2012)。为了更直观地表达样方之间的差异性, 距离矩阵又可以通过降维排序(ordination) 得到一个二维的排序图(Legendre & Gallagher, 2001; Tuomisto, 2010) (图1)。排序的方法包括主坐标分析(principal coordinates analysis, PCoA, 等同于经典多维尺度变换classical multidimensional scaling, MDS)、非度量多维尺度分析(non-metric multidimen-sional scaling, NMDS)等。
本文的其它图/表
|