自然界的生物群落虽呈现各种复杂的动态, 但各物种却又能在一定程度上实现共存, 从而具有稳定性。在20世纪70年代之前, 人们综合野外观察、控制实验、数学模型、理论解释等多个角度的研究, 认为群落的稳定性与复杂性之间存在正的关联。在对自然群落的观察方面, Odum (1953)发现陆地生态系统中简单群落的种群密度波动比一般群落更剧烈。Elton (1958)指出人工的单作系统容易发生害虫暴发; 岛屿生境易被入侵; 物种较少的寒带群落的种群波动明显, 而物种丰富和复杂的热带雨林则显得更稳定。在控制实验方面, 实验生态系统中的捕食者-猎物系统会发生剧烈的振荡并通常很快灭绝。数学模型也显示, 捕食者-猎物系统的简单数学模型不存在稳定的局部平衡点, 一般会陷入振荡或者灭绝(Elton, 1958; Pimentel, 1961)。在理论机制方面, MacArthur (1955)指出, 如果某个物种与多个捕食者或猎物相关联, 则它不至于因个别物种密度的波动而引致大的变动。虽然也有一些不同的观点(Goodman, 1975), 但复杂的群落更稳定这一观点得到了当时多数生态学家的认同。
然而到了70年代, May (1972b, 1973)对数学模型的分析结果却表明复杂程度的提高总体而言将导致不稳定性增加。这一论断与前述结果相矛盾, 然而看上去它们却又都是对的, 一时间人们莫衷一是, “悖论”由此产生, 并引发群落生态学中的“复杂性-稳定性论辩” (The Complexity-Stability Debate) (Margalef, 1975; Mcnaughton, 1977)。
近半个世纪以来, 人们在自然群落分析(Paine, 1980)、控制实验(Fagan, 1997)、数学模型等多个方面的大量研究已大大深化了对这一问题的整体认识(Bersier, 2007), 并已发表不少综述文献(Pimm, 1984; McCann, 2000; Jansen & Kokkoris, 2003; Landi et al, 2018)。国内对该领域的综述相对较少, 其中有的年代较早(黄建辉和韩兴国, 1995; 张晓爱和邓合黎, 1996), 且主要是对一些结论或相关机制的概括性介绍(马风云, 2002; 王国宏, 2002; 高东和何霞红, 2010), 而对于数学模型方面, 仅见陈云峰等(2014)对土壤食物网研究进展的介绍。本文对该论题的数学模型方面的研究进展进行简要综述, 以对这一空缺加以填补。首先, 对复杂性和稳定性的含义加以辨析, 以澄清论题; 然后介绍主要的模型研究方法, 包括基于线性交互的群落矩阵方法和基于非线性交互的多种方法; 最后对这一领域的研究方向进行展望。
1 论题解析
对论题本质的剖析以及对“复杂性”和“稳定性”等相关概念的准确界定是这一研究的前提, 然而它们却恰恰各自具有多种不同的含义(Grimm & Wissel, 1997)。在某种程度上, 正是概念的混淆使得这一论辩一度陷入了越辩越不清的境地。
1.1 论题本质
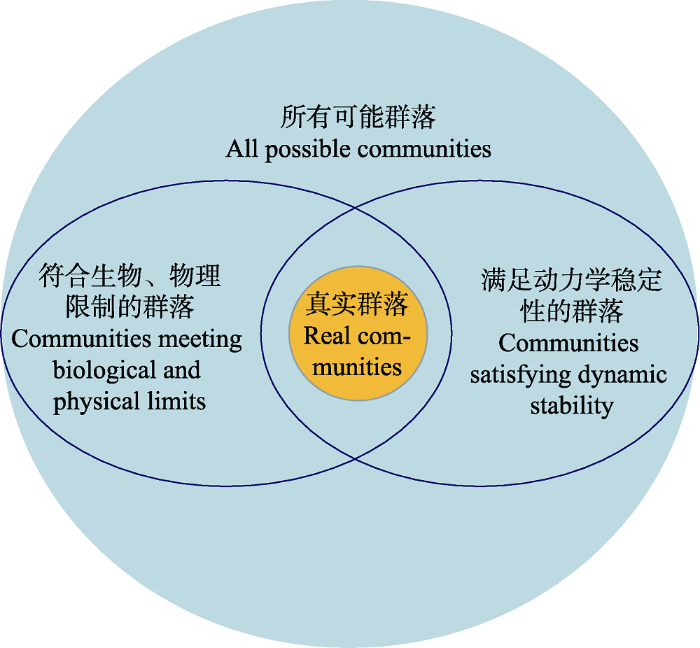
从根本上说, 复杂性-稳定性关系之争反映了当时群落生态学中实践与理论之间尚存在巨大鸿沟(Dunne et al, 2015)。实际上, “悖论”的始作俑者May本人就已给出了一种解释: 虽然复杂的随机群落很可能不稳定, 但自然生态系统可能存在一些迂回策略(devious strategies), 使得复杂性和稳定性可以共存, 而生态学家的任务就是揭示这些机制(May, 1973)。从这个意义上来说, 复杂性-稳定性论题的本质是探求自然界中各物种是如何相互作用并实现长期共存的(Rohr et al, 2014)。自然界中真实存在的群落只是可能群落集合中的极小一部分, 之所以绝大部分可能群落都没有出现, 首先是因受到各种生物和物理因素的限制, 其次是因不具备动力学稳定性而不能长期存在, 最后就是纯粹的概率原因(Pimm, 1982)。复杂性‒稳定性研究一般从两个方向入手: (1)从现实群落入手, 它们具有怎样的格局(pattern), 其生物学和动力学稳定性的机理是什么? (2)从可能的群落入手, 稳定的群落应具有怎样的格局, 这些格局能否被现实的生物学限制满足(图1)?
图1
1.2 复杂性
自然群落中的物种除了种内作用之外, 还通过竞争、捕食、寄生、共生等方式发生两两间相互作用, 这些相互作用构成了一个网络, 可用一个0/1矩阵描述。除了网络结构之外, 物种间的相互作用还具有不同的强度, 这样就需要一个实数矩阵。在物种数较多的情况下, 这已是错综复杂, 然而却还远不是问题的全部。物种的相互作用并非固定不变, 而是受到密度制约、空间因素、时滞效应、高阶相互作用、行为的适应性改变等的影响, 体现为各种非线性函数, 从而不再是一个矩阵元素所能表示, 而需要多个参数。巨大的复杂性使得精确把握复杂群落的动态成为不可能。而复杂性‒稳定性论题则正是试图找出一种化繁为简的模式, 即通过群落的少数几个属性来推断其整体稳定性, 具体的指标可包含多种(Landi et al, 2018)。而这又取决于所采用的模型类别, 不同类型的模型依赖于不同的假设, 有不同的结构, 所涉及的相关属性也不尽相同。
早期研究一般采用群落矩阵方法(即假设物种间为线性相互作用), 主要关注3种属性, 即多样性(物种数)、连接度和平均相互作用强度, 这些属性被统称为复杂性。而在观测和实验研究中, 则常用多样性来代表复杂性, 这是因为在自然生态系统中, 往往难以确认两物种间是否存在相互作用(实验中观察越细致, 往往会发现更多原先被忽略的弱连接(Loreau et al, 2001))。此时, 对影响群落动态的其他各种因素都做了大量的简化。不同的研究采用的模型不同, 其隐含的假设也不同, 复杂性的含义也不尽相同。May (1972b)得出随机群落s(nC)1/2 < d (n为物种数, C为矩阵连接度, s为种间相互作用强度, d为种内相互作用强度, 详见2.1.1小节)的稳定性判据, 就是假设每个物种的种内作用是确定的, 而物种之间是否存在相互作用是随机的, 当存在相互作用时, 其强度也是随机的。在这些假设条件之下, 物种数、连接度以及种内和种间平均相互作用强度之比决定了模型群落的局部稳定性。这一结果可以解读为: 随着群落变得复杂, 对相互作用强度扰动的耐受性将减小。
随着研究越来越深入, 且对模型所做的假设越来越符合实际, 人们发现了很多与稳定性相关的其他属性, 包括网络的拓扑结构以及具体相互作用强度的不同分配格局等。虽然这些属性已不属于复杂性的范畴, 但这些研究都源自复杂性‒稳定性研究, 属于May所说的“迂回策略”, 对它们的探索正是议题的一部分。更进一步的研究则要求拓宽群落矩阵的范围, 采用非线性的相互作用, 以及引入显式的空间等, 此时就有必要引入新的更多的指标来刻画系统的相关格局(Delmas, 2019)。
1.3 稳定性
“稳定性”引起的概念混淆比“复杂性”有过之而无不及(Orians, 1975; Connell & Sousa, 1983)。有时, 对同一系统应用不同的稳定性概念可能会得出相反的结果。例如, 单一种植的植物在其自身密度的微小扰动之后, 凭借其高生长速率能迅速恢复, 即高弹性(resilience), 然而因其高生长速率与其高可食性相关, 故对入侵的食草动物也非常敏感, 因此具有低抵抗力(resistance) (McCann, 2010)。
自然系统中各种因素都处在变化之中, 但变化速度快慢和相互关系是不同的, 反映在数学模型上, 就是系统的状态变量和参量的区别。变化较慢且本身不受系统内部其他因素影响的因子一般作为参量(环境变量), 反之则作为状态变量。对群落建模时一般以各种群的密度(或数量)作为状态变量, 而相互作用结构以及作用强度方面的系数(如内禀增长率和捕食效率等)则作为模型参量。群落稳定性也相应地分为状态稳定性(参量不变, 对状态变量扰动)和结构稳定性(对参量扰动)。复杂性‒稳定性论题所指的实际上是结构稳定性, 即模型群落能稳定共存的参数空间的大小, 这一参数空间越大, 就意味着系统的整体稳定性越高, 该系统也就越具有现实可能性(Rohr et al, 2014)。从这个意义上说, 人们所考虑的是一个模型的族, 而非单个模型。不过上述参量与变量的区分也并非绝对。 例如, 在一些研究中, 网络结构也被当作状态变量(某些种群可以灭绝), 并以结构的改变程度(最终群落中共存的物种数与初始群落物种数之比)作为稳定性的度量(Brose et al, 2006; Thébault & Fontaine, 2010)。还有一类特殊的结构性扰动是物种入侵或去除, 但对这一领域的探讨超出了本文的范围。
在给定参数值之后, 模型就已被确定, 从理论上说系统的行为(从而也包括其稳定性属性)就已决定了, 但此时仍存在如何度量这一稳定性的问题。此时就需要借助前述的状态稳定性概念, 如抵抗力和弹性就属于这一层面, 它们可作为探索稳定性的工具(Grimm, 1996; Grimm & Wissel, 1997; Donohue et al, 2016)。在最基本的意义上, 稳定意味着持久(persistence), 即关注的重点在于群落中的物种是否持续共存, 而它们的数量变化则相对次要(Lewontin, 1969; Connell & Sousa, 1983; Anderson et al, 1992; Berlow et al, 2004)。在数学上, 度量持久性的一种方法是所有物种具有正丰度的状态空间区域内系统轨迹的有界性, 其对应的概念是永久性(permanence) (Schuster et al, 1979; Law & Morton, 1993; Jansen & Sigmund, 1998)。即如果稀有物种的丰度趋于增加, 则系统更具持久性。以常微分方程组给出的动力系统为例(Hutson和Schmitt (1992)还考虑了各种其他动态):
其中, x = (x1, x2, …, xn)T表示群落中各物种的种群密度。如果边界(包括所有坐标轴的正半轴和无穷远处的点)是排斥的, 则称这种系统是永久性的(Jansen & Sigmund, 1998)。
但永久性概念在实际应用中难以处理, 于是就有了一些替代性的方案, 其中局部稳定性(local stability)在过去相当长的时间内被大量应用(Holling, 1996; Chen & Cohen, 2001)。然而, 局部稳定性概念有很多不足: (1)环境扰动通常是剧烈的, 局部稳定但缺乏永久性的系统是脆弱的(Townsend et al, 2010); (2)自然系统是不平衡的, 种群的持续存在不要求所有轨道都收敛于内部平衡点(Townsend et al, 2010), 它还可以是极限环、奇怪吸引子(strange attractor)等(陈兰荪等, 1988; Law & Blackford, 1992; Morton et al, 1996; Kendall et al, 1999)。总体而言, 以局部稳定性表示的群落共存的参数空间远小于持久性(Anderson et al, 1992)。
永久性概念也有其自身的局限, 例如种群的随机波动(demographic stochasticity)可能会将丰度较小的种群推向灭绝(Townsend, 2009)。于是变率(variability)就成为衡量稳定性的另一个重要指标, 变率越大则越容易造成种群出现低丰度的情形。吸引子本身可具有不同程度的稳定性, 一般来说, 规则的吸引子(如不动点)的稳定性高于不规则吸引子(如奇怪吸引子)。同一类型的吸引子中稳定性也有差别, 例如对于极限环的振荡, 波动幅度更小则意味着系统更稳定(McCann, 2000; Ives & Carpenter, 2007)。从更一般的意义上说, 状态空间中会存在多个不同类型的吸引子, 其中有的是可行的(feasible, 所有物种的数量或密度都大于零, 即具有正的丰度), 另一些则不可行, 而状态空间也因而被划分为多个吸引域, 对稳定性的评判须基于这些吸引子的形状以及其吸引域大小的信息。
2 主要模型方法及进展
通过数学模型方法研究复杂性‒稳定性问题的基本步骤一般是先建立模型框架, 再确定可变参数及其变化范围, 并给出评判状态空间稳定性的方法。现实群落巨大的复杂性使得模型研究不得不进行简化, 包括模型结构和参数的取值。按照相互作用类型, 可以将模型大致分为线性(即群落矩阵法)和非线性两类, 它们分别可包括多种具体的方法。需要注意的是, 即使是形式上属于同一类型的模型, 由于背后不同的假设, 参数的意义也不同, 对结果的解读也就不同。例如群落矩阵法, 既可以作为真实生态系统在接近平衡态时的模拟(此时矩阵元素表示相互作用强度, 具有生态学意义); 也可以作为更复杂系统的线性近似(此时矩阵元素的生态学意义不明确)。而Lotka-Volterra模型也同样如此: 它既可以看作是更复杂系统处于非平凡平衡点(nontrivial equilibrium)时各物种个体增长率的线性化(Lotka, 1925), 也可以被视为适用于全局的动力学方程(Volterra, 1926; Pimm, 1982; Haydon & Lloyd, 1999; Townsend, 2009)。下面对这几类主要方法及其进展加以简要介绍。
2.1 线性模型
这类模型的本质是抛开群落中各物种间的具体相互作用方程, 直接从雅可比矩阵入手, 从而将大量的群落信息封装到一个相对简单的矩阵中, 通过其最大特征值实部是否为负来考察其局部稳定性。这一方面是由于早期缺乏真实群落的结构和物种间相互作用强度数据, 另一方面也是便于数学处理而不受网络规模的限制(May, 1972b)。雅可比矩阵的来源则如前所述, 可能是假设自然群落存在平衡, 考察其物种间相互作用的结构和强度而得到; 也可能是将1.3节的方程(1)在平衡点线性化得到。需要注意的是, 后者会有可行性问题, 即该平衡点的各物种丰度是否都为正(详见2.2.1小节)。这一领域的研究相对较为充分, 根据赋参方法的不同包括随机群落矩阵法(只给出物种数、连接度、平均相互作用强度, 而具体的网络拓扑结构和相互作用强度则随机给出), 以及探索不同网络拓扑结构和相互作用强度分布对稳定性影响的方法。
2.1.1 随机相互作用
在早期的研究中, 由于缺乏经验数据来锚定模型, 故随机交互是一个合理的起点。May (1972b)将Gardner和Ashby (1970)用于大型系统动力学稳定性研究的随机网络模型加以发展并引入群落生态学, 开创了随机群落矩阵方法。群落矩阵M的元素通过如下步骤确定: (1)每个非对角元素以1-C的概率取0值(C为矩阵连接度, 表示任意两物种间存在相互作用的概率); (2)对于非零元素, 其值随机取自均值为0、方差为s的一个分布(表示种间相互作用强度); (3)对角线元素设为d (负值, 表示存在种内密度制约)。一旦取样, 就可通过检查该矩阵的主特征值实部是否为负, 得出该矩阵对应的群落是否具有局部稳定性。通过重复的随机取样, 可得到大量的随机群落矩阵, 并求出稳定网络的百分比(percentage of stable webs, PSW) (Allesina & Tang, 2015)。当n较大时, 若满足s(nC)1/2 < d, 则群落几乎完全稳定, 否则几乎完全不稳定(May, 1973; Allesina & Tang, 2012)。也就是说, 随着复杂程度的增加, PSW趋于减小。
早期关于复杂性与稳定性关系的研究多数采取了这一方法(Pimm & Lawton, 1977; Neutel et al, 2002)。随着随机矩阵理论(random matrix theory, RMT)这一数学分支的发展, 解析地求出主特征值的范围在很多情况下变得可行, 从而拓展了群落矩阵方法的应用(Anderson et al, 2010; Bai & Silverstein, 2012; Tang et al, 2014; Allesina & Tang, 2015)。通过在受限范围内进行取样, 随机矩阵方法可以在一定程度上引入食物网的结构和相互作用强度属性。例如, “捕食者‒猎物”型网络中, Mij的符号与Mji相反, 可通过对这一对系数联合采样得到群落矩阵。Allesina和Tang (2012)发现系数均值为零的3种相互作用形式(纯随机、捕食者‒猎物、互惠+竞争)中, “捕食者‒猎物”型网络稳定的可能性最高, 而“互惠+竞争”形式稳定的可能性最低。而在相互作用强度分布方面, 弱相互作用对“捕食者‒猎物”型食物网络具有不稳定效应, 对互惠和竞争网络(及其混合物)具有稳定效应, 而对随机网络没有影响(Allesina & Tang, 2012)。
2.1.2 有结构网络
与随机群落矩阵不同, 现实中的群落都有一定的结构(Dunne et al, 2002)。例如, 实际存在的食物网几乎是非循环的, 几乎都具有区间结构(interval structure), 即一组捕食者的猎物中的重叠模式可以表示为沿着一条线的可重叠的区间(Lawlor, 1978; Williams & Martinez, 2000; Stouffer et al, 2006); 具有分室结构(compartments), 即群落可以分为若干子集, 同一子集内物种间存在相互作用的可能性较高, 而跨越子集边界的交互则较少(Allesina & Pascual, 2010; Stouffer & Bascompte, 2011); 营养级数量一般有限; 捕食、竞争、互惠等关系都是成对出现的等等(Townsend et al, 2010; Allesina & Tang, 2015)。实际上, 实际存在的生态网络只是可能性集合中的沧海一粟。例如, 在一个随机组织的含n个物种的群落中, 不存在不合理的三物种环路的可能性, 对于n = 10、20、30、40和60, 概率分别大约为10-2、10-16、10-56、10-137和10-472 (Lawlor, 1978)。因此, 考察群落的各类不同结构对于稳定性的效应就成了很多研究的主题(Yodzis, 1981; de Ruiter et al, 1995; Emmerson & Raffaelli, 2004)。
(1)分室结构。很多经验研究指出食物网具有分室结构(Pimm & Lawton, 1980; Moore & Hunt, 1988; Raffaelli & Hall, 1992; Solow & Beet, 1998)。May (1972b; 1973)认为分室结构的模型食物网具有更高的稳定概率。Pimm和Lawton (1980)通过模拟发现, 对于生物学上合理的模型且连接度相同的情况下, 分室结构通常是不利于稳定的, 其结果与May (1972b; 1973)的结论相反(Solow et al, 1999)。不过, 这些研究针对的是生境内部, 而食物网中的分室可能因不同生境边界的限制而产生(Pimm, 1982)。近年来的研究表明, 食物网分室结构主要与环境中的亚生境(Krause et al, 2003)、群落内的系统发育模式(Cattin et al, 2004; Rezende et al, 2009), 以及不同的能量通道(Zhao et al, 2017)有关。此类分室结构显然是稳定的, 但原因可能在于其本身的复杂度较低(连接度小, 作用强度低)。此外, 分室结构可以跨越多个层次, 表现为等级系统, 而且上层对下层也会有稳定性作用(McCann, 2010)(详见2.2.3小节)。
(2)营养一致性(trophic coherence)。Pimm等对一些具有生物学合理结构的中等规模网络的研究发现, 总体而言, 对于一个稳定的模型食物网来说, 杂食现象不应广泛存在, 且杂食者不应以不相邻营养水平的物种为食(Pimm & Lawton, 1978; Pimm, 1980)。当时的理论解释是, 在其他条件相同的情况下, 杂食的增加意味着复杂性增加, 导致模型稳定的可能性降低(Pimm, 1982)。而近年来关于网络结构的研究则揭示这一问题可采用食物网的营养一致性来解释。营养一致性是衡量节点如何整齐地分为不同层次的指标, 它可减少网络中反馈环的数量, 提高稳定性(Johnson et al, 2014)。而杂食(尤其是以多个营养级为食)将降低网络的营养一致性。Johnson和Jone (2017)应用营养一致性作为指标, 将各种网络划分为高反馈和低反馈两个不同的区域, 并通过与零模型的对比说明了其对于局部稳定性的重要性。对于相关的生物学机制则需要进行进一步的研究, 初步推测为可能存在进化压力, 使得捕食者在狭窄的营养水平范围内选择其猎物(Johnson & Jone, 2017)。
(3)供体控制(donor-control)。供体控制模型与一般的捕食者‒猎物模型的区别在于只存在猎物对捕食者的单向正面作用, 而捕食者对猎物的丰度则几乎没有影响。在自然界中有多种情形符合这类的营养关系, 如某些捕食者只猎取年老和病弱的猎物、食腐动物的存在以及碎屑食物链等。供体控制模型中不存在反馈环, 因而通常是稳定的, 并且其局部稳定性与增加的复杂性无关, 从而可以达到相当高的复杂程度(de Angelis, 1975; Pimm, 1982)。
2.1.3 相互作用强度格局
生态网络中的相互作用强度结构对于群落稳定性至关重要(Haydon, 2000; Kokkoris et al, 2002)。在随机矩阵模型中, 物种间相互作用的大小取自一个均值为0、方差为δ的随机分布。而在真实生态系统中, 相互作用强度的范围可跨越若干个数量级(Wootton, 1997), 并且分布通常倾向于弱相互作用(Paine, 1992; Goldwasser & Roughgarden, 1993; de Ruiter et al, 1995; Fagan, 1997)。多种生物学机制对网络权重的格局进行了限制, 使其表现为倾斜分布。例如, 对捕食者‒猎物体型比的限制(Cohen et al, 1993)、物种‒区域关系(Harte et al, 1999)、代谢标度关系(West et al, 1997)、体型与活动范围的关系(Schoener, 1968)等。通过研究这些机制如何将相互作用格局限制在某个子集内, 可以为理解网络结构和动力学之间的联系提供一个整体框架(Berlow et al, 2004)。
其中, 取食关系的等级限制(Cohen, 1989; Williams & Martinez, 2000)对食物网的稳定性提供了有力解释(Neutel et al, 2002; Emmerson & Raffaelli, 2004)。假设杂食动物的捕食强度随猎物生物量而变化, 即其捕食低营养级的猎物多, 捕食较高营养级的猎物少, 其结果将导致整个食物网在较长的环中总是存在相互作用强度较弱的连接, 环的权重也就较小, 从而有助于食物网的整体稳定。营养层次每提高一级, 生物量需减少10倍方可提供稳定性所需的相互作用强度的模式, 因而金字塔侧面的斜率可能是网络稳定性的良好指标(Neutel et al, 2002; Raffaelli, 2002; Neutel & Thorne, 2014)。
2.2 非线性模型
如前所述, 群落矩阵模型是对现实系统进行大量简化后的结果。复杂性‒稳定性“悖论”的一种可能原因是, May当时所使用的线性稳定性并没有捕捉到生态系统动力学的基本特征。许多后续研究工作开始探索更精确的动力学描述将对稳定性产生何种影响, 这些方法仍处于探索阶段, 下文分别加以阐述。
2.2.1 相互作用矩阵方法
群落矩阵方法直接从雅可比矩阵入手, 其元素是单位相互作用强度与种群密度的乘积, 从而略去了群落中各物种间的每单位相互作用(per capita interaction)方式。由于无法知道平衡点时群落中的各种群密度, 因此该方法实际上隐含地假设了平衡点的各种群密度都为正(即具有可行性), 而可行性显然是与局部稳定性同等重要的稳定性属性。因此, 对于群落矩阵方法得出的结论在多大意义上能反映现实一直存在很多的质疑(Roberts, 1974; Vandermeer, 1975; Kokkoris et al, 2002; Rohr et al, 2014)。模型方法的进一步发展意味着逐步摒弃不够合理的假设, 代之以更多符合实际的信息。这首先就需要回到原始相互作用方程, 即给出Lotka-Volterra方程的参数aij和bi, 计算得到平衡丰度(X*)并检查是否都为正(Christianou & Kokkoris, 2008)。这种方法所采用的交互方式可以是随机或具有结构, 而交互强度一般仍取自随机分布, 稳定性的评价是可行性和局部稳定性, 需要求出平衡点和计算矩阵特征值, 一般可适用于大中型网络(Pimm, 1982)。
Roberts (1974)将内禀增长率设定为单位向量, 发现在可行的情况下, 随机群落几乎都是局部稳定的。而后续相关研究则发现, 若令内禀增长率向量取自随机分布, 则得到的可行群落的局部稳定性概率却几乎为零, 而且, 随着平均相互作用强度和群落中物种数量的增加, 可行性概率迅速下降(Gilpin, 1975; Goh & Jennings, 1977; Pimm, 1982)。Christianou和Kokkoris (2008)采用具有承载力的竞争型Lotka-Volterra方程, 并改进了抽样方法, 发现在可行的前提下, 简单和复杂的竞争群落可以具有相同的稳定概率, 并且复杂群落可耐受比简单群落更高的相互作用强度方差。然而, 这些研究中的种群内禀增长率向量都是随机或给定的。新近研究表明, 对于Lotka-Volterra方程所描述的群落, 对任何给定的相互作用矩阵, 都可以设置一个给定的可行平衡点, 然后计算相应的内禀增长率向量。反之, 如果随机给出内禀增长率向量, 则将不太可能得到一个可行的群落(Saavedra et al, 2017)。对于小的随机组合群落, 可行性和稳定性是相互作用矩阵和内禀生长率向量相结合的结果, 两者都与物种丰富度有关, 并非所有固有增长率的抽样分布都会导致相同的稳定性和可行性概率。可行性并不总是能保证稳定性, 在可行性领域内, 还可以找到不稳定的内在增长率向量(Song & Saavedra, 2018)。对于大型系统, Dougoud等(2018)通过一个可调节相互作用强度的Lotka-Volterra模型发现, 在中等相互作用强度下(即May, 1972b的情形), 对于所考虑的任何模型, 物种丰富的系统中都不存在可行的平衡; 而在弱相互作用时, 随机结构系统可同时满足可行性和局部稳定性准则。Stone (2018)对于密度制约型增长群落(density-dependent community, Lotka-Volterra模型是其中一个典型例子)的研究表明, 在平衡点为可行的前提下, 如果相互作用矩阵是稳定的, 则线性化后得到的群落矩阵也将是稳定的。类似结论也由Gibbs等(2017)通过不同方法得出。
2.2.2 复杂网络数值模拟法
相互作用矩阵方法虽比随机群落方法有所进步, 但仍只采用了最基本的Lotka-Volterra模型(不包含复杂的功能反应类型), 以及在平衡点处进行局部稳定性分析的方法。然而在复杂性‒稳定性研究中, 非线性因素十分重要, 即使是普通的捕食者‒猎物系统的数学模型, 也往往出现极限环等非平衡行为(May, 1972a)。由于此时可能会存在多个平衡点, 以及其他类型的吸引子, 使得上述平衡点局部稳定性方法的结论可靠性变低。随着研究的深入, 出现了一些只需通过使用较少的参数就可生成接近真实食物网的拓扑结构的方法。包括食物网中的级联模型(cascade model) (Cohen et al, 1990; Solow & Beet, 1998)、生态位模型(niche model) (Williams & Martinez, 2000)、嵌套层次模型(nested-hierarchy model) (Cattin et al, 2004)、互惠网络中的嵌套结构(nested architectural pattern) (Bascompte et al, 2003; Olesen et al, 2007; Bascompte, 2009)及寄生网络中的逆生态位模型(inverse niche model) (Warren et al, 2010)等。另一方面, 计算机技术的发展也使得非线性数值模拟变得可行。于是, 人们开始将一些原先用于描述两物种交互的模型推广到复杂网络, 并采用数值方法对其动力学行为进行模拟研究。该方法一般是给出初态之后, 让模型运行一个给定的时间步数(充分长以达到定态), 然后通过考察最终状态的一些指标来给出稳定性的度量。其所考察的指标为是否所有物种都保持正丰度, 以及最终共存的物种数与初始时物种数之比(Brose et al, 2003)。
Williams和Martinez (2007)采用基于Yodzis和Innes (1992)的相互作用方程, 对随机、级联和生态位3种食物网结构进行了动态模拟, 发现随着物种数和连接度的增加, 各模型的持久性呈线性下降, 从而在完全不同的模型环境中定性地复现了May (1972b)的结果。在三种网络拓扑结构中, 随机结构最终维持的物种最少; 级联模型模拟了几种自然网络特性(如营养级的划分), 约50%的初始物种得以最终维持共存; 而生态位模型模拟了十几种网络特性, 其持久性也有了进一步提高。Rohr等(2014)采用Bastolla等(2005)的模型, 对不同互惠网络结构的结构稳定性进行了研究。其结果表明, 结构稳定性与嵌套性和互惠强度呈正相关, 与互惠权衡呈二次函数关系。而通过对比发现, 得到最大稳定性的参数组合所描述的网络结构与实际观察到的互惠网络最接近。Thébault和Fontaine (2010)用一个具有Holling II型功能反应的消费者‒资源模型和一个具有饱和效应的互惠模型, 对食物网和互惠网络进行了系统比较。结果发现, 对于互惠网络, 高连接度和嵌套结构有利于稳定; 而食物网则要求模块化和弱相互作用, 这与对实际群落的观察结果相符(Thébault & Fontaine, 2010)。这些研究表明, 更准确地描述自然群落结构的模型通常具有更高的持久性。
除了网络结构之外, 人们也开始寻找一些对相互作用强度分布进行简单参数化的更符合实际的方法。体型大小作为决定物种新陈代谢速率和行为模式等的一个因子, 对食物网的格局具有重要影响 (Emmerson & Yearsley, 2004)。例如, Brose等(2006)将体型大小作为依据参数化了一个非线性的相互作用模型, 发现捕食者‒猎物质量比率的变化所解释的种群和食物网稳定性的变化比物种多样性、食物网结构、代谢类型或功能反应的变化更多。这些结果表明, 在自然界中发现的捕食者‒猎物的体型比率可能是维持复杂食物网中种群数量和自然生态系统多样性的关键。由于体型比与食物网稳定性之间的正相关似乎是由于单位生物量的间接相互作用强度降低所致, 因此这一解释与经典线性稳定性理论的观点一致, 即降低平均相互作用强度有助于提高食物网的稳定性(Brose et al, 2006)。
2.2.3 食物网构件动力学
对非线性种群动态模型的数值模拟, 为我们理解多物种系统的动态稳定性提供了重要的依据(Dunne et al, 2005)。然而这一方法对稳定性的探索显然只是粗浅的, 更精细的分析需要考察种群的波动程度, 描述相空间中的各种吸引子和吸引域大小, 而这又受制于浩繁的计算量而只适用于中小型系统。不过至少对食物网而言, 一个显著特征是重复性构件(modules)结构(McCann, 2000), 于是可采取先充分理解构件或子网, 然后将各构件组合起来逐渐勾勒整个群落动态的办法。而这一研究方法也是由May首先倡导的(May, 1973; McCann, 2010)。此类模型包括的细节最丰富, 对参数的取值也更符合实际情形(包括相互作用方式和作用强度参数的各种取值可能), 同样也采用数值模拟方法, 以种群的波动程度作为稳定性的度量(如McCann et al, 1998)。
构件是食物网的子系统模型, 一般是2-4个物种之间竞争和捕食的组合(例如链状结构和表观竞争为两种常见的3物种构件), 其不同于图式(motif)之处在于除拓扑结构外, 还内含相互作用强度(McCann, 2010)。构件动力学实际就是对微型食物网的逼真模拟, 此时, 群落动力学通常所使用的具有非饱和I型功能反应的线性Lotka-Volterra方程通常被认为是对自然的过度简化(Brose et al, 2003; Christianou & Kokkoris, 2008), 而相互作用强度及其分布作为模型参数对食物网动态的影响逐渐受到人们的重视(Jonsson & Ebenman, 1998; Haydon & Lloyd, 1999; Kokkoris et al, 2002; Emmerson & Yearsley, 2004)。构件理论正是通过模拟实验分析稳定性(永久性和变率)随着相互作用强度而发生的变化。
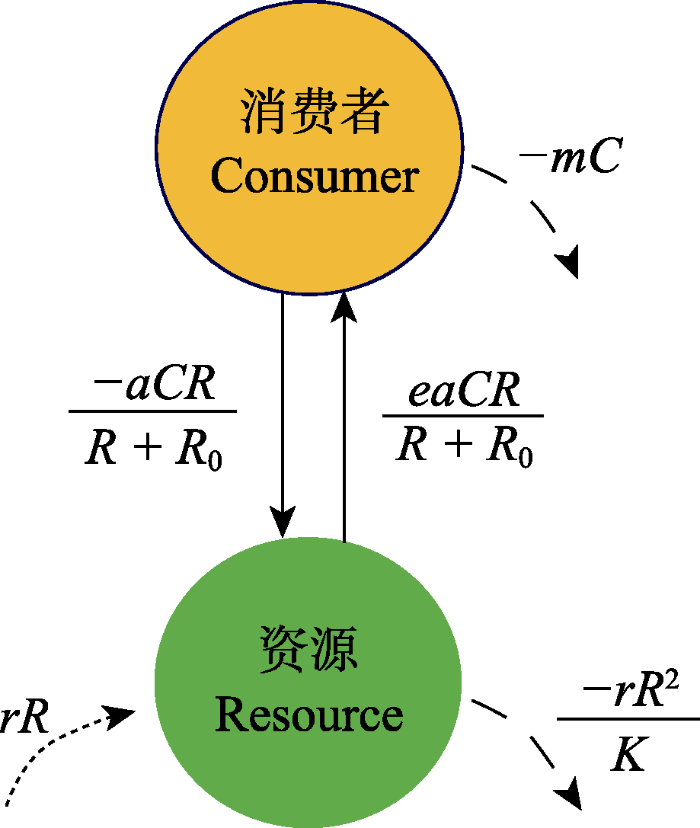
McCann (2010)将种群的动态区分为非激发(non-excitable)和可激发(excitable)两类: 前者在局部扰动后单调地接近平衡的动态轨迹, 而后者以振荡方式接近平衡或振荡吸引子的动态轨迹。对于前者, 增加通量会使其更快地恢复到给定的平衡密度; 而对于后者, 生产力的增加会产生过冲动态并推迟稳态的到来(McCann, 2010)。例如, 在单种群的Logistics模型中, 如果种群动态为单调趋向其承载力K, 则随着内禀增长率r的增加而稳定性增加(弹性更大); 而如果种群动态是振荡的(如在离散或时滞情况下), 则随着r的增大, 振荡幅度也会增加, 从而更不稳定。在此基础上, McCann (2010)对Rosenzweig-MacArthur (R-M)型消费者‒资源(consumer‒resource, C‒R)系统(Rosenzweig & MacArthur, 1963)进行了剖析(图2)。
图2
图2
消费者-资源相互作用(改绘自McCann, 2010)。其中R和C分别表示资源和消费者种群密度, r为资源内禀增长率, K为承载力, a为攻击率, R0是资源的半饱和密度, e是转化为消费者生物量的比例, m为消费者的个体死亡率。
Fig. 2
Consumer-resource interaction (redrawing from McCann, 2010). Where R and C are population density of the resource and consumer, respectively, r is intrinsic growth rate of resource, K is the carrying capacity, a is the attack rate, R0 is the semi-saturation density of resource, e is the proportion converted to the consumer biomass, and m is mortality rate of consumer.
R-M模型中的3类物质流动方式: (1)耦合项(图2中连接C、R的实线); (2)损耗项(图2中短划线, 包括消费者的线性损耗项-mC和资源受制于承载力的-rR2/K项); (3)资源吸收项(图2中虚线, rR项)。C-R相互作用中任何参数对变量的动态响应取决于耦合项相对于损耗项的强度, 耦合强度的增加往往会使已激发的C-R相互作用不稳定(McCann, 2010)。在3物种构件模型中, 弱相互作用可通过以下3种自然机制来抑制潜在的振荡子系统: (1)表观竞争(apparent competition): 消费者可以通过权衡改变消费倾向, 转向第二种资源, 降低消费者攻击第一资源的效率, 从而抑制潜在的振荡性C-R交互; (2)剥削性竞争(exploitative competition): 较弱的第二消费者减少了共享资源的增长率, 从而抑制第一消费者在与资源交互中潜在的振荡; (3)食物链捕食: 顶级捕食者可以抑制中间消费者的增长速度, 从而抑制其与资源的交互(即营养级联效应(trophic cascade), Oksanen et al, 1981)。
类似稳定机制在其他类型相互作用方式中也存在, 例如在竞争网络中, 当物种不能在一个简单的线性竞争层次中排序时, 就会发生不可递(intransitive)竞争。此时减少循环中任一竞争者的数量都会通过网络传播。对于具有奇数个物种的系统, 反馈将有利于受扰动物种的恢复, 从而具有稳定作用(May & Leonard, 1975; Allesina & Levine, 2011; Levine et al, 2017)。
整个食物网可视为一组相互作用的构件, 通过合理布局来容纳生物多样性(Michio, 2008)。稳定食物网既可以由稳定的构件组成, 也可通过一些机制使不稳定构件稳定化而达成, 如弱相互作用对强相互作用的弱化, 以及消费者对异步资源动态(asynchronous resource dynamics)的平均化(McCann, 2010)。
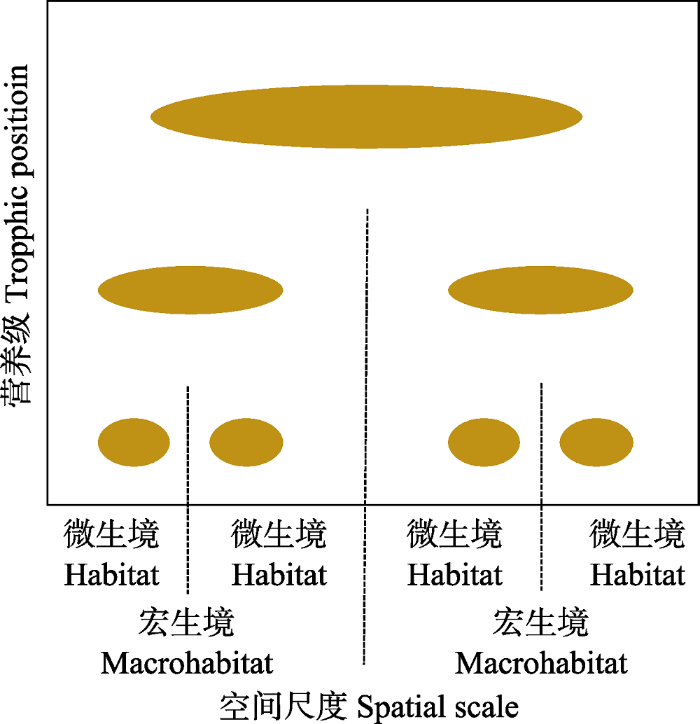
如前所述, 除了网络拓扑意义上的分室结构, 还存在相互作用强度意义上的分室结构(即分室之内以较强的方式相互作用, 而之间以弱相互作用连接)。真实生态系统中, 相互作用强度的范围可跨越若干个数量级(Wootton, 1997), 并且分布通常倾向于弱相互作用(Paine, 1992; Goldwasser & Roughgarden, 1993; de Ruiter et al, 1995; Fagan, 1997), 已证实食物网具有分室结构(Krause et al, 2003)。一些理论研究也说明构件之间的弱连接可以起稳定作用(Teng & McCann, 2004)。McCann等(2005)发现, 一些小型消费者将来自微生境的资源耦合起来, 大型消费者将宏观生境中的资源耦合起来, 通过在各个空间尺度上重复这一营养结构, 形成了嵌套形式的分室结构, 即等级结构, 并在景观尺度上表现出稳定的群落动态。耦合者一般是能够快速响应于底层构件变异性的捕食者, 在调节食物网动态中起着关键作用(图3)。
图3
图3
食物网的空间等级结构。椭圆表示各营养级物种的空间尺度及其所覆盖的栖息地(改绘自McCann, 2010)。
Fig. 3
The spatial hierarchy structure of food web. Ellipses indicate the spatial scale of each trophic level and the habitat it covers (redrawing from McCann, 2010).
2.3 小结
综上所述, 不同模型方法基于不同的假设, 采取不同的策略, 以及不同的稳定性定义(表1)。总体而言, 线性模型结构简单, 易于进行稳定性分析, 但难以真实有效反映自然群落中的复杂相互作用; 非线性模型则相反。在随机相互作用的情况下, 各类模型基本上复现了May (1973)的结果, 即稳定性随着复杂性增加而降低。然而人们也发现了一些基于现实生态网络格局的模型具有很好的稳定性。这些稳定性的机制包括: 较强的种内密度制约作用、食物网的营养一致性结构、供体控制以及弱相互作用等。对于线性模型而言, 这些机制都反映在其群落矩阵的构成中。局部稳定性意味着群落矩阵的所有特征值实部为负, 在数学上, Routh-Hurwitz准则确立了判断任意给定矩阵的特征值是否都具有负实部的充要条件, 其主要工具是矩阵特征多项式系数构造的Hurwitz行列式序列, 而特征多项式的各个系数: a1, a2, a3, …, an, 表示系统的n阶反馈, 于是这一准则就可与系统中的反馈相联系起来。其大致的对应关系为: 首先, 系统中的各阶反馈总体上都表现为负反馈; 其次, 高阶反馈不存在或者较弱(Levins, 1974; Dambacher et al, 2003; Neutel & Thorne, 2014)。上述的线性模型稳定性机制都可以从这两条得到解释。而非线性的情形显然要复杂得多: 一方面, 在线性模型中得到的结果能在多大程度上向非线性模型推广显然是个重要的问题; 另一方面, 非线性模型本身又会有线性模型不具备的稳定性机制。
表1 复杂性‒稳定性研究模型方法
Table 1
| 方法名称 Approach name | 群落构建方法 Community construction method | 群落规模 Community size | 稳定性衡量 Stability measurement |
|---|---|---|---|
| 群落矩阵法 Community matrix approach | 指定物种数、连接度、平均相互作用强度, 随机给出或指定网络结构和相互作用分布 Species number, connectivity, average interaction intensities are designated; web structure and interaction distribution rule are random or designated | 适用大型生态网络 Suitable for large ecological networks | 局部稳定性, 稳定网络的百分比(PSW) Local stability, percentage of stable webs (PSW) |
| 相互作用矩阵法 Interaction matrix approach | 指定物种数, 网络结构可随机给出或指定, 随机给出每单位相互作用强度 Species number is designated, web structure can be designated or random, per unit interaction intensities are random | 适用大中型生态网络 Suitable for large and middle-sized ecological networks | 局部稳定性+可行性, 稳定网络的百分比(PSW) Local stability and feasibility, percentage of stable webs (PSW) |
| 复杂网络的数值模拟法 Numerical simulation of complex network | 指定物种数, 网络结构由专门模型生成, 相互作用强度参数通过与体型比给出, 或在一定范围内变动 Species number is designated, web structure is generated by model, parameters of interaction intensity are given by the ratio to body size, or vary within a certain range | 适用中型生态网络 Suitable for middle-sized ecological networks | 持久性(共存的物种数占比) Persistence (the proportion of coexisting species) |
| 食物网构件动力学法 Food web module dynamics approach | 所有参数都直接指定 All parameters are designated | 适用小型构件, 但可通过构件组合推测大型食物网的稳定性 Suitable for small web module, but could be used to infer the stability of large food webs | 永久性+波动程度 Permanence and variability |
3 结论与展望
3.1 结论
在当今各门学科的发展中, 数学模型一方面是理论的载体, 另一方面也越来越成为与实验手段并列的科学探索工具。在复杂性‒稳定性论题中, 由于对实际生态网络的经验研究的困难和滞后, 模型的作用更加突出。经过近半个世纪的努力, 人们对于自然界群落的复杂动态也有了更为真切的认识, 对复杂性‒稳定性“悖论”也有了合理的解释。除了复杂性和稳定性本身的多重含义之外, “悖论”的产生还有两方面的原因。其一, Elton (1958)以及Odum (1953)等主要是基于对真实群落的观察而得出复杂的群落更稳定, 然而这些早期的观察尚不够全面和深入, 且像农田单作系统是受人为控制的, 不能代表自然群落。例如, Jacquet等(2016)对全球各地116个定量食物网进行了稳定性分析, 发现经典的复杂性相关属性与真实食物网的稳定性无关。其二, May (1973)是通过对模型群落的研究得出复杂性不利于稳定性结论的, 然而这些模型群落与真实群落的情形有很大的不同。模型研究需要事先给出合理的参数, 或至少要大致知道参数的分布, 如果只是任意选取参数, 则很可能得出错误结论。而早期模型(如随机群落矩阵方法)对参数的选取往往不够合理, 没有排除掉不符合生物和物理方面限制的模型, 于是也就难以得出一致的结论。实际上May本人在其1973年的经典著作中就已指出数学模型的结果与实际情况不符并不意味着悖论, 因为自然界中的实际情况并非数学模型所表示的那么简单和任意, 复杂性本身并不能带来稳定性, 后者来自于自然界在长期的演化过程中形成的某些特殊结构(May, 1973)。而后来的研究者们也确实在大量探索之后发现了很多网络结构, 以及相互作用方式和强度方面的稳定性机制(如Pimm, 1982; McCann et al, 1998)。
引言中提到, MacArthur在论证复杂性有利于稳定性时曾提出一个简单而有吸引力的理论: 能量在流经食物网时的选择越多(复杂性), 则当一个或多个物种具有异常高或低丰度时(扰动), 物种丰度(稳定性)的变化就越小(MacArthur, 1955)。然而, 这种稳定性高度依赖于交互强度和异步的资源动态, 强交互作用或者同步的资源基础无助于维持消费者的稳定(McCann, 2010)。但在现实群落中, 多样化的资源对干扰的响应一般不会是同步的, 因此, 具有更多资源获取途径的物种波动更少, 即稳定的子系统可以起到约束潜在不稳定子系统的作用。例如, 虽然大多数杂食系统可能是局部不稳定的(Pimm & Lawton, 1978), 但弱杂食系统却具有强稳定性(McCann, 2010)。
总体而言, 生物学因素的限制和动力学稳定性的要求共同塑造了自然界的群落格局。在一些情形下, 生物学因素的限制使得系统中物种与环境以及物种之间的交互方式和参数只能在一个较小的范围内取值, 而在此范围内, 系统的动力学稳定性也恰好能得到满足, 如分室结构、弱相互作用(Neutel et al, 2002)。而在另一些情况下, 则生物学可能还不足以提供解释, 如营养一致性, 此时动力学稳定性可能起着更重要的作用。
3.2 展望
对于复杂性‒稳定性的研究还远未结束, 我们所探索到的仍只是整个可能性空间的极小一部分, 自然界所发展出的复杂而又稳定的系统(例如雨林、珊瑚礁等)的能力仍令人惊叹。
一方面, 目前的模型尚未能有效反映真实的自然系统, 需要进一步发展。在模型基本结构方面, 近期研究发现生态系统中的高阶相互作用对稳定性具有不可忽视的效应(Bairey et al, 2016; Levine et al, 2017; Mayfield & Stouffer, 2017)。在网络类型方面, 当前模型研究一般将生态网络划分为不同类型(食物网、互惠网、寄生网等)来研究, 而自然界中, 这些网络是交织在一起的。研究表明, 不同交互类型组成的复合网络有助于系统稳定性(Mougi & Kondoh, 2012; Bachelot et al, 2015)。在空间异质性方面, 异质空间环境中复合生态系统(meta-ecosystem)的空间动力学可具有强大的稳定效应(Gravel et al, 2016)。
另一方面, 稳定性的概念也有必要拓展。首先, 在永久性的前提下, 生态群落也可能存在多个吸引子或运行状态(dynamic regime) (Scheffer et al, 2001; Fath et al, 2003)。例如, Allesina和Tang (2015)发现, 群落不同的多度分布会对局部稳定性产生影响。其次, 在各种稳定性概念的关系方面, Townsend等(2010)和Gibbs等(2017)的研究表明, 局部稳定性概念比原先认为的有更强的适用性, 然而这方面的探索仍较缺乏。第三, 从长期来看群落并非静态实体, 而是一直处于流变之中, 网络结构、相互作用强度乃至物种组成都可在一定范围内改变, 具有一定的灵活性和适应性, 此时可能涉及到更高层次的稳定性(如生产力、养分循环等生态系统属性), 一种更好的描述视角可能是复杂适应系统(Levin, 2005)。
复杂性‒稳定性研究具有多方面的意义。从应用角度上, 稳定的生态群落为生态系统服务提供重要支撑, 也是生态系统管理的重要目标。例如, 生境破碎化将导致食物网被压缩在小块生境内, 从而导致各物种间的耦合强度增大, 引发系统不稳定并造成生物多样性减少; 类似地, 物种的丢失也会因食物网的萎缩而增大物种间的交互强度, 造成震荡等不稳定现象(McCann, 2000)。从理论角度上, 当前关于生物多样性研究的几个方向, 如物种共存理论、生物多样性与生态系统功能理论以及复杂性与稳定性理论, 仍处于各自独立发展的阶段, 期待未来它们之间会产生交叉融合, 乃至形成关于生物多样性的更为综合和统一的理论。此外, 复杂性‒稳定性研究的方法和理论成果还将为我们理解其他复杂系统提供有益的启发和借鉴。
参考文献
Food web models: A plea for groups
A competitive network theory of species diversity
The stability‒complexity relationship at age 40: A random matrix perspective
An Introduction to Random Matrices
On the conditions for permanence of species in ecological communities
Interactions among mutualism, competition, and predation foster species coexistence in diverse communities
Spectral analysis of large dimensional random matrices
High-order species interactions shape ecosystem diversity
The nested assembly of plant-animal mutualistic networks
Biodiversity in model ecosystems. I. Coexistence conditions for competing species
Interaction strengths in food webs: Issues and opportunities
A history of the study of ecological networks
Comment on “Foraging adaptation and the relationship between food-web complexity and stability”
Allometric scaling enhances stability in complex food webs
Phylogenetic constraints and adaptation explain food-web structure
Permanence in ecosystems
种群生态系统的持续生存
Global stability, local stability and permanence in model food webs
Research progress on ecosystem complexity-stability relationships based on soil food web
基于土壤食物网的生态系统复杂性‒稳定性关系研究进展
Complexity does not affect stability in feasible model communities
Food webs and community structure
Community Food Webs: Data and theory
Body sizes of animal predators and animal prey in food webs
On the evidence needed to judge ecological stability or persistence
Qualitative stability and ambiguity in model ecosystems
Energetics, patterns of interaction strengths, and stability in real ecosystems
Analysing ecological networks of species interactions
Navigating the complexity of ecological stability
The feasibility of equilibria in large ecosystems: A primary but neglected concept in the complexity-stability debate
Modeling food-web dynamics: Complexity-stability implications
Food-web structure and network theory: The role of connectance and size
Weak interactions, omnivory and emergent food-web properties
Predator-prey body size, interaction strength and the stability of a real food web
Omnivory as a stabilizing feature of natural communities
Regime changes in ecological systems: An information theory approach
Research advances on biodiversity and ecosystem stability
生物多样性与生态系统稳定性研究进展
Connectance of large dynamical (cybernetic) systems: Critical values for stability
The effect of population abundances on the stability of large random ecosystems
Feasibility and stability in randomly assembled Lotka-Volterra models
Construction and analysis of a large Caribbean food web
The theory of diversity-stability relationships in ecology
Stability and complexity in model meta-ecosystems
A down-to-earth assessment of stability concepts in ecology: Dreams, demands, and the real problems
Babel, or the ecological stability discussions: An inventory and analysis of terminology and a guide for avoiding confusion
Self-similarity in the distribution and abundance of species
Maximally stable model ecosystems can be highly connected
On the origins of the Lotka- Volterra equations
Engineering resilience versus ecological resilience
Biodiversity and ecosystem stability
生物多样性和生态系统稳定性
Permanence and the dynamics of biological systems
No complexity-stability relationship in empirical ecosystems
Complexity and stability revisited
Shaken not stirred: On permanence in ecological communities
Trophic coherence determines food-web stability
Looplessness in networks is linked to trophic coherence
Effects of predator-prey body size ratios on the stability of food chains
Why do populations cycle? A synthesis of statistical and mechanistic modeling approaches
Variability in interaction strength and implications for biodiversity
Compartments revealed in food-web structure
Complexity and stability of ecological networks: A review of the theory
Self-assembling food webs: A global viewpoint of coexistence of species in Lotka-Volterra communities
Alternative permanent states of ecological communities
A comment on randomly constructed ecosystem models
Self-organization and the emergence of complexity in ecological systems
Beyond pairwise mechanisms of species coexistence in complex communities
Biodiversity and ecosystem functioning: Current knowledge and future challenges
Research advances on ecosystem stability
生态系统稳定性若干问题研究评述
Fluctuations of animal populations and a measure of community stability
Diversity, stability and maturity in natural ecosystems
Stability and Complexity in Model Ecosystems
Nonlinear aspects of competition between three species
Data from higher-order interactions capture unexplained complexity in diverse communities
Weak trophic interactions and the balance of nature
The dynamics of spatially coupled food webs
Diversity and stability of ecological communities: A comment on the role of empiricism in ecology
Building trophic modules into a persistent food web
Resource compartmentation and the stability of real ecosystems
On models for assembling ecological communities
Diversity of interaction types and ecological community stability
Stability in real food webs: Weak links in long loops
Interaction strengths in balanced carbon cycles and the absence of a relation between ecosystem complexity and stability
Exploitation ecosystems in gradients of primary productivity
The modularity of pollination networks
Diversity, stability and maturity in natural ecosystems
Food webs: Linkage, interaction strength and community infrastructure
Food-web analysis through field measurement of per capita interaction strength
Species diversity and insect population outbreaks
Number of trophic levels in ecological communities
Are food webs divided into compartments?
Compartments and predation in an estuarine food web
Compartments in a marine food web associated with phylogeny, body mass, and habitat structure
On the structural stability of mutualistic systems
Graphical representation and stability conditions of predator-prey interactions
A structural approach for understanding multispecies coexistence
Catastrophic shifts in ecosystems
Dynamical systems under constant organization. III. Cooperative and competitive behavior of hypercycles
On an early result on stability and complexity
Will a small randomly assembled community be feasible and stable?
The feasibility and stability of large complex biological networks: A random matrix approach
Compartmentalization increases food-web persistence
A robust measure of food web intervality
Correlation between interaction strengths drives stability in large ecological networks
Dynamics of compartmented and reticulate food webs in relation to energetic flows
Stability of ecological communities and the architecture of mutualistic and trophic networks
On the generality of stability-complexity relationships in Lotka-Volterra ecosystems
The Stability of Model Ecosystems
Interspecific competition: A new approach to the classical theory
Fluctuations in the abundance of a species considered mathematically
Further thoughts on diversity and stability in ecosystems
再论生物多样性与生态系统的稳定性
The inverse niche model for food webs with parasites
A general model for the origin of allometric scaling laws in biology
Simple rules yield complex food webs
Dynamic network models of ecological diversity, complexity, and nonlinear persistence
Estimates and tests of per capita interaction strength: Diet, abundance, and impact of intertidally for aging birds
Body size and consumer-resource dynamics
Ecosystem organization: Food chain dynamics and mutualism‒cybernetics
生态系统的组织理论: 食物链动态论与互惠共生‒控制论
Identifying compartments in ecological networks based on energy channels