20世纪50年代以来, 围绕着多样性与稳定性的关系展开了激烈的争论。早期曾有多样性导致稳定性的论点(MacArthur, 1955; Elton, 1958)。近期研究发现多样性与稳定性的关系较为复杂(Wang & Loreau, 2016; Liao et al, 2017), 大致可分为正相关、不相关和负相关三类。亦有研究报道稳定性与多样性的非线性关系, 如Taffi等(2015)以平均路径长度为指标研究了网络的稳定性, 发现在不同作用条件下物种移除与网络稳定性均呈现非线性的关系。多样性与稳定性的关系可能与稳定性的定义有关。稳定性是多层次概念, 包括持久性(persistence, 在一定边界范围内保持恒定或维持某一特定状态的持续时间)、抵抗性(resistance, 在外部扰动下维持其原状态的能力)、恢复性(resilience, 被干扰改变状态后回到其原状态的能力)和稳健性(robustness, 在受到干扰后抵抗灭绝的能力) (Saint-Béat et al, 2015)。其中, 稳健性侧重考虑生态系统抵御灭绝的能力。在人类活动导致全球生境破碎化进而增加物种灭绝风险的背景下, 这一性质显得尤为重要(Aguilar et al, 2006; Stone, 2010)。
稳健性是存在内外部干扰时, 系统抵抗灭绝、维持功能的能力(Stelling et al, 2004; Kitano, 2007), 对于反映物种间营养相互作用, 理解群落结构与动态具有重要意义(Hastings et al, 2016)。稳健性研究主要依靠野外实验与模型模拟方法。野外实验主要是物种去除实验, 即去除某个或几个物种后观察食物网的变化(孙刚和盛连喜, 2000)。模型模拟则是利用计算机去除食物网某个或几个节点以及它们之间的联系, 通过计算食物网节点间连通情况得到稳健性(Zhao et al, 2016)。
野外去除实验与模型模拟研究均发现, 在维持食物网结构稳定方面某些物种可能发挥更重要的作用。这些物种的活动与多度对群落组成与结构有决定性影响, 被称为关键种(Paine, 1969; 韩兴国等, 1995)。后续研究中关键种的概念被泛化和模糊。有研究将移除后导致次生灭绝最快发生的物种当作关键种(Dunne et al, 2002); 有研究将在低营养级中发挥重要作用的物种称为关键种(孙龙启等, 2016);亦有研究将去除后导致食物网急剧变化的物种作为关键种(Kadoya et al, 2018)。鉴于此, 有必要给出关键种的定量依据。食物网关键种的定量判定方法不仅有助于揭示食物网中物种关系, 而且有利于对关键物种进行优先保护。
网络里度的性质反映网络结构, 去除某些节点可影响网络中其他节点的连通。网络连通的能力与食物网连接稳健性概念类似。连接稳健性是指食物网在节点去除后仍能够保持连通的能力(杜巍等, 2010)。因此, 可通过计算连接稳健性, 判断物种在食物网中的重要程度。关键种与非关键种在维持食物网连接稳健性方面的表现可能有差异, 即关键种丧失导致的食物网连接稳健性降低程度可能高于非关键种丧失导致的食物网连接稳健性降低程度。这一差异可作为检验关键种与非关键种划分的依据。
利用度的性质研究网络稳健性已有报道。Solé和Montoya (2001)通过分析网络中节点间的连接数量研究了陆地与淡水生态系统食物网的稳健性。Zhang等(2016)研究了节点连接数是否可作为反映网络稳定性的可靠指标。网络里度的性质可体现在多个方面, 常用指标有点度中心度(degree centrality, DC)、紧密中心度(closeness centrality, CC)、中介中心度(betweenness centrality, BC)。点度中心度表示与节点直接相连的节点数目, 点度中心度越大, 表明与该节点直接相连的节点越多。紧密中心度表示节点到其他所有节点的距离, 紧密中心度越大, 说明节点越处于靠近中心的位置。中介中心度表示节点位于两两连通节点的最短路径的比例。本研究尝试从多个度的指标角度开展食物网稳健性研究。
本研究首先通过计算网络中表征度性质的多个指标对物种进行分类, 进而利用不同类物种对食物网连接稳健性影响程度的差异, 区分关键种与非关键种, 最后分析不同节点去除方式下, 节点数量对食物网连接稳健性的影响, 以期为如何判定关键种贡献新的思路。
1 材料与方法
1.1 数据来源
本研究所用食物网数据来源于Interaction Web DataBase (https://www.nceas.ucsb.edu/interactionweb
/resources.html.), 该数据来自Thompson和Townsend在新西兰南岛Catlins河流调查的水生昆虫、藻类和鱼类共49个物种构成的食物网(Thompson & Townsend, 2005)。不同物种间相互作用通过邻接矩阵表示。当矩阵元素为1时, 表示物种i和物种j之间存在直接相互作用, 当矩阵元素为0时, 表示物种i和物种j之间不存在直接相互作用。
1.2 节点中心性
本研究计算了表征节点度的性质的三个指标, 即点度中心度(DC)、紧密中心度(CC)、中介中心度(BC)。计算公式如下:
其中, liv表示节点i和节点v之间的边的条数, dvi表示点v和点i之间的最短距离, gij表示联系点i和点j之间最短距离边的数目, givj表示联系点i和j最短距离边中经过点v的边的数目(唐毅, 2017)。以上计算过程利用Python实现。
1.3 节点分类
本研究采用基于模型的聚类方法。该方法利用混合高斯模型(GMM), 认为数据服从正态分布, 每个正态分布由K个高斯分布组成, 每个高斯分布称为一个组成部分, 这些组成部分线性加成在一起就组成了GMM的概率密度函数。在不指定聚类数的情况下, 根据数据推出概率密度分布, 自动选择最优聚类数。本部分的计算利用R语言中的mclust包完成(Scrucca et al, 2016)。
1.4 食物网稳健性
自然界中通过去除实验确定关键种的方法可通过模拟实现, 存在随机去除和确定性去除两种方式(Memmott et al, 2004)。随机去除主要是模拟自然界中物种随机消失, 而确定性去除主要是根据物种重要程度有针对性地去除某些物种。本文中随机去除是首先对节点编号, 利用生成随机数的方式确定待去除节点编号, 根据节点编号出现顺序依次确定要去除的节点。本研究中的确定性去除考虑了两种情况, 即按重要程度从大到小去除(降序去除)与从小到大去除(升序去除)。这里的重要程度指对节点按其中心度性质排序, 中心度高的节点被认为更重要。
去除节点后, 计算食物网的连接稳健性。连接稳健性衡量食物网在节点去除后仍能够保持连通的能力。其计算公式为:
式中, N表示初始网络的规模, Nr表示从网络中去除的生态节点个数, C表示当生态节点被去除后生态网络中最大连通子图中的节点个数(于强等, 2018)。为避免随机去除节点对网络稳定性的影响, 随机去除方式下, 计算过程重复进行10,000次, 取平均值作为连接稳健性结果。不同去除方式对网络稳健性影响的计算利用Python实现。
2 结果
2.1 节点分类
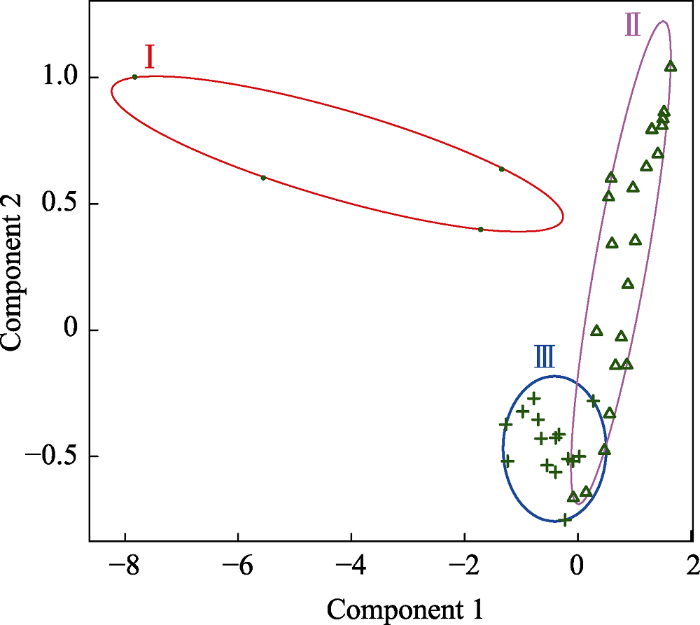
本研究以点度中心度、中介中心度、紧密中心度为指标, 对食物网各节点进行聚类, 以贝叶斯信息量(BIC)作为聚类依据。结果表明, 节点可聚为3类(n = 49, BIC = 648.069), I、II、III类包含的节点数目分别为4个、30个、15个(图1)。I类节点具有相对较高的点度中心度、中介中心度、紧密中心度; II类节点上述3个指标的值相对更低; III类节点相对应指标的值介于前两者之间。每个类的点度中心度、中介中心度、紧密中心度的均值、方差、中位数、最大值、最小值见表1。I类节点包含物种为碎屑、植物材料、弯楔藻和南乳鱼类, 其余两类节点包含的物种有碎屑、藻类、水母、海胆、昆虫、虾、鱼等。三类物种在营养级上的区别不大。
图1
表1 节点的点度中心度、中介中心度、紧密中心度的汇总统计量
Table 1
| 类别 Cluster | 指标 Indices | 均值 Mean | 方差 Variance | 中位数 Median | 最大值 Maximum | 最小值 Minimum |
|---|---|---|---|---|---|---|
| Ⅰ类 | 点度中心度 DC | 0.394 | 0.027 | 0.383 | 0.575 | 0.234 |
| 中介中心度 BC | 0.216 | 0.028 | 0.180 | 0.428 | 0.078 | |
| 紧密中心度 CC | 0.538 | 0.012 | 0.528 | 0.662 | 0.435 | |
| Ⅱ类 | 点度中心度 DC | 0.047 | 0.001 | 0.043 | 0.106 | 0.021 |
| 中介中心度 BC | 0.003 | 0.000 | 0.001 | 0.011 | 0.000 | |
| 紧密中心度 CC | 0.386 | 0.002 | 0.398 | 0.465 | 0.305 | |
| Ⅲ类 | 点度中心度 DC | 0.116 | 0.001 | 0.106 | 0.170 | 0.064 |
| 中介中心度 BC | 0.036 | 0.001 | 0.031 | 0.083 | 0.003 | |
| 紧密中心度 CC | 0.469 | 0.000 | 0.470 | 0.500 | 0.431 |
2.2 节点性质与连接稳健性关系
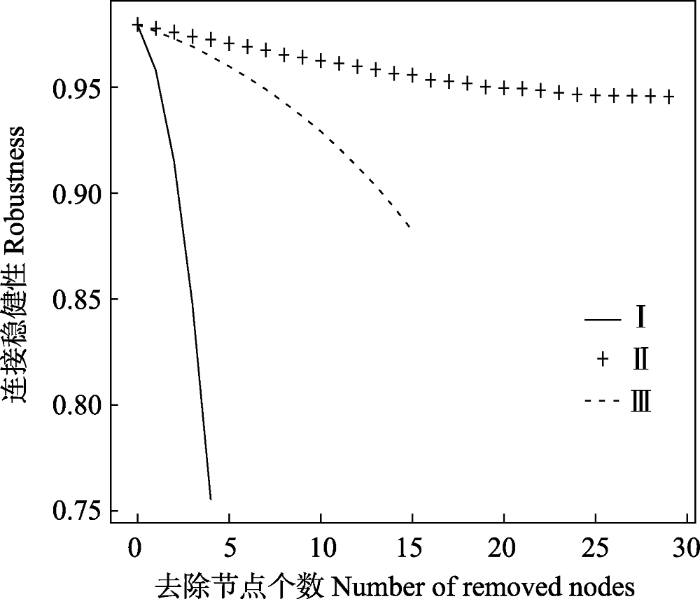
去除这三类节点对连接稳健性下降具有不同程度的影响。去除I类节点, 食物网的连接稳健性迅速降低; 去除II类节点, 随着去除节点数量增加, 连接稳健性变化较小, 去除III类节点, 随着去除节点个数的增加, 食物网连接稳健性逐渐降低, 降低的速率小于I类节点, 大于II类节点(图2)。
图2
图2
分类去除节点数目与连接稳健性的关系
Fig. 2
The relationship between the connectivity robustness and the number of removed nodes
2.3 节点数量与连接稳健性
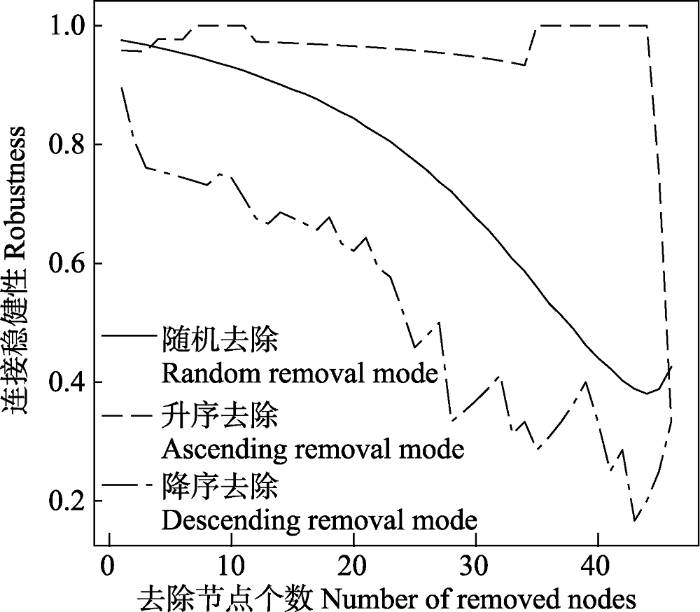
随机去除方式下, 去除节点数量增加时, 连接稳健性呈先降后增的趋势, 最小值为0.38, 对应的去除节点数量为44。降序去除方式下, 连接稳健性先波动式下降, 当去除节点数量为43时, 连接稳健性达到最小值; 其后, 连接稳健性逐渐增加。升序去除方式下, 去除节点数量为44时, 连接稳健性出现显著变化。此前, 连接稳健性基本呈缓慢降低趋势; 此后, 连接稳健性急剧降低(图3)。
图3
图3
不同去除方式下的节点数量与连接稳健性的关系
Fig. 3
The relationship between the robustness and the number of removed nodes under different removal modes
3 讨论
本研究表明, 食物网中节点度的性质存在明显差异。根据聚类结果, 可将Catlins河流的食物网中物种分成三类: I类节点个数较少且具有相对较高的中心度, II类节点个数最多且具有相对较低的中心度, III类节点个数和中心度介于其余两类节点之间。其中I类与其他两类物种相比, 具有较高的点度中心度、中介中心度和紧密中心度。较高的点度中心度、中介中心度和紧密中心度表明I类节点在网络中处于较为核心的地位, 可认为是更加重要的物种。通过模拟随机去除实验发现, 不同物种在维持稳健性方面的重要程度确有差异。去除I类物种, 食物网稳健性迅速降低; 去除II类物种, 食物网稳健性变化较小; 去除III类物种, 食物网稳健性有所降低, 但降低速率介于二者之间。这表明, I类物种对食物网稳健性影响最大, II类物种对食物网稳健性影响最小, III类物种对食物网稳健性的影响介于二者之间。这意味着I类物种即为食物网中的关键种。
本研究计算食物网中节点度的性质, 以此为指标进行聚类分析, 根据聚类分析结果判定关键种。这一方法定量确定了食物网中的关键种, 为关键种的判定提供了新的思路。值得指出的是, 本研究中的I、II、III类物种在营养级上并无明显区分。这意味着关键种并不总是处于营养级顶端。这一结果与早期研究认为的关键种应处于食物网顶端营养级的结论不同(Paine, 1966), 支持关键种的概念可用于不同营养级中的物种。
去除方式对食物网连接稳健性也有影响。第一, 随机去除方式下, 食物网连接稳健性的值高于降序去除方式下的食物网连接稳健性。这一结果与Solé等(2001)的结果一致。他们发现, 随机去除节点比降序去除节点方式下的食物网能维持更高的稳健性。可能的原因在于降序去除方式可能导致更大程度的次生灭绝。第二, 随机去除与降序去除方式下, 食物网连接稳健性均呈先减小后增加的抛物线趋势, 其极小值点出现的位置比较接近(去除节点数量分别为43、44)。升序去除方式下, 连接稳健性小幅波动, 待去除节点数量为44时, 连接稳健性急剧减小。三种去除方式下, 该食物网连接稳健性发生显著变化对应的去除节点数量均为43或44, 这可能与关键种完全丧失有关。这意味着关键种在维持食物网稳健性方面发挥了重要作用。第三, 升序去除方式下, 连接稳健性呈降低趋势; 降序去除与随机去除方式下, 连接稳健性在持续减小后又有小幅度增加。这一结果与Taffi等(2015)的结果不同。Taffi等(2015)发现, 降序去除方式下食物网稳健性逐渐降低。本研究发现, 降序去除方式下稳健性呈抛物线式变化, 即先减后增。一种可能的解释为, 食物网中物种丧失导致食物网结构重构, 即单个节点消失, 使得食物网其他物种间可能构建新联系或者改变原有连接路径。如食物网中某物种灭绝将导致其捕食者加大对其他被捕食者的捕食强度(李医民等, 2014)。第四, 升序去除方式下的食物网连接稳健性减小速率低于随机去除与降序去除方式下的连接稳健性减小速率。这可能与物种丧失的先后顺序有关。升序去除方式下, 重要程度低的物种先丧失; 降序去除方式下, 重要程度高的物种先丧失; 随机去除方式下, 每个物种丧失的概率相同。丧失的物种数量相等时, 重要程度高的物种对食物网影响高于重要程度低的物种。
选择网络中表征度性质的不同指标可能影响食物网稳健性研究结果。Zhang等(2015)比较物种去除数量变化与中介中心度、卡茨中心度的关系, 发现两种中心度对物种去除数量的响应存在差异。本研究利用多个表征度性质的指标, 可反映食物网中节点性质的不同方面。本研究中对物种重要程度的排序依据中心度大小, 并且将点度中心度、紧密中心度、中介中心度看作具有相同权重的指标。但三种中心度指标在测量网络结构时有侧重。点度中心度衡量与节点直接相连的节点数目, 紧密中心度衡量每个结点到其他结点的最短路径的平均长度, 中介中心度衡量经过某个节点的最短路径数目。在不同的网络结构中, 三种中心度的重要程度可能有差异。因此计算物种重要程度时, 存在根据网络结构特点调整中心度权重的可能性。
4 结论
本研究发现不同类的物种在维持食物网稳健性方面有差异。I类物种对食物网连接稳健性影响最大, II类物种对食物网稳健性影响最小, III类物种对食物网稳健性影响介于二者之间。其中I类物种对应该食物网中的关键种。本研究为如何判定关键种贡献了新的思路。
去除方式对食物网连接稳健性有影响。升序去除方式下, 连接稳健性呈降低趋势; 降序去除与随机去除方式下, 连接稳健性在持续减小后又有小幅度增加。可能在于物种丧失导致食物网物种间建立新联系或改变原有连接路径。三种去除方式下, 食物网连接稳健性发生显著变化对应着几乎相同的去除物种数量, 可能与关键种完全丧失有关, 表明关键种在维持食物网稳健性方面发挥重要作用。
致谢: 感谢责任编委与审稿专家提出的修改建议。
参考文献
Plant reproductive susceptibility to habitat fragmentation: Review and synthesis through a meta-analysis
Study on indices of network structure robustness and their application
网络结构鲁棒性指标及应用研究
Network structure and biodiversity loss in food webs: Robustness increases with connectance
The significance and problems of key concepts in biodiversity conservation
关键种概念在生物多样性保护中的意义与存在的问题
Introduction to the special issue: Theory of food webs
Potential oscillators and keystone modules in food webs
Towards a theory of biological robustness
Ecosystem stability and ecological diversity based on complex networks
基于复杂网络的生态系统稳定性与生态多样性
Robustness of metacommunities with omnivory to habitat destruction: Disentangling patch fragmentation from patch loss
Fluctuations of animal populations and a measure of community stability
Tolerance of pollination networks to species extinctions
Food web complexity and species diversity
A note on trophic complexity and community stability
Trophic networks: How do theories link ecosystem structure and functioning to stability properties? A review
mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models
Complexity and fragility in ecological networks
Robustness of cellular functions
Key species theory of ecosystem: New ideas, new mechanisms, new ways
生态系统关键种理论: 新思想、新机制、新途径
Study on the structure and function of ecosystem in Northern Beibu Gulf VII: Nutrition structure construction and key screening based on ecopath model
北部湾北部生态系统结构与功能研究VII: 基于Ecopath模型的营养结构构建和关键种筛选
Bioaccumulation modelling and sensitivity analysis for discovering key players in contaminated food webs: The case study of PCBs in the Adriatic Sea
Research on traffic node setting in Northeast China under the background of “Belt and Road”
“一带一路”背景下东北地区交通节点设置研究
Energy availability, spatial heterogeneity and ecosystem size predict food-web structure in streams
Biodiversity and ecosystem stability across scales in metacommunities
Research on spatial ecological network structure based on complex network analysis
基于复杂网络分析法的空间生态网络结构研究
Stability of food webs to biodiversity loss: Comparing the roles of biomass and node degree
Weighting and indirect effects identify keystone species in food webs