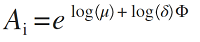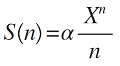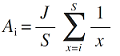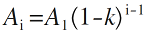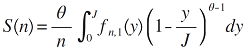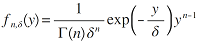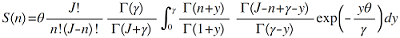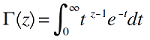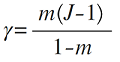群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 )。作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 )。从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 )。一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 )。对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 )。
马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾。Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 )。Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布。自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表。MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model)。在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型。生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 )。当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 )。
自然界中, 常绿与落叶物种是较易辨识的两类植物生活型。前者的换叶过程是逐步发生的, 因而从生态外貌上看它们一年四季都是绿色的; 而后者的“新叶”却通常在“老叶”集中掉落后才会生出, 期间有时会相隔数月。常绿和落叶物种作为常绿阔叶林内两种重要的生活型组分(Song, 1988 ; 宋永昌和王祥荣, 1995 ), 对其物种多度分布格局进行分析, 将有助于我们从新的视角理解常绿阔叶林内物种多样性的形成与维持机制。以天童20 ha常绿阔叶林样地内的常绿与落叶物种为例, 前者作为样地中的优势组分, 物种多度最大的细枝柃(Eurya loquaiana )共计20,414株, 常绿稀有种(多度≤ 1株/ha)有18个, 占常绿物种总数的24.66%; 落叶物种中多度最大的南酸枣(Choerospondias axillaris )仅有1,352株, 落叶稀有种则有37个, 占到落叶总物种数的46.84%。基于此, 我们假设: (1)在天童常绿阔叶林中, 常绿与落叶物种的物种多度分布之间应该有着较为明显的差别; (2)主导两者物种多度分布及各自多样性格局形成的生态学过程可能会有所不同。
本文首先对天童20 ha常绿阔叶林样地内常绿与落叶物种的物种多度分布曲线进行比较, 以判断它们之间的差异性; 进而选择了6种常用模型对两者的多度数据进行拟合, 旨在揭示和对比常绿与落叶物种多度分布格局背后的生态学过程及其异同点, 为深入理解亚热带常绿阔叶林内生物多样性的维持机制提供基础。
1 材料与方法
1.1 研究区域概况
研究样地位于浙江天童国家森林公园内, 距离宁波市区28 km。区域内气候为典型的亚热带季风性气候, 夏季炎热多雨, 冬季寒冷干燥(宋永昌和王祥荣, 1995 ; Wang et al, 2007 )。根据宁波市鄞州区气象站的记录, 本地年平均温度为16.2°C, 最热月和最冷月分别出现在7月(平均温度28.1°C)和1月(平均温度4.2°C)。区域内的年均降水量为1,374.7 mm, 主要集中于每年的5-8月(宋永昌和王祥荣, 1995 )。
1.2 样地的建立与调查
天童20 ha常绿阔叶林动态监测样地建成于2010年, 位于森林公园的核心区域(29°48.817ʹ N, 121°47.116ʹ E)。样地内的植物群落结构完整, 发育成熟, 为典型的中亚热带常绿阔叶林(杨庆松等, 2011 ; 宋永昌等, 2015 )。整个样地东西长500 m, 南北宽400 m, 地形较为复杂(杨庆松等, 2011 )。
样地内所有胸径(DBH) ≥ 1 cm的木本植物均鉴定到种, 调查时测量其胸径并挂牌, 同时记录它们在样地内的坐标(杨庆松等, 2011 )。在2010年的调查中, 共记录到木本植物152种, 隶属51科96属, 总计94,605株(杨庆松等, 2011 )。
1.3 样地中的常绿与落叶物种
前述的152个物种当中, 包括了79种落叶与73种常绿木本植物(杨庆松等, 2011 )。虽然常绿物种在物种丰富度方面不及落叶物种, 但它在多度(8,6371株)、胸高断面积(421,9057 cm2 )和重要值(79.9)方面却占据着绝对优势。样地内个体密度≤ 1株/ha的稀有物种共有55种, 其中落叶的有37种(杨庆松等, 2011 )。
就物种多样性而言, 若从整个样地的水平进行对比, 落叶种(Shannon-Wiener指数: 3.250; Simpson指数: 0.936)要稍高于常绿种(Shannon-Wiener指数: 2.906; Simpson指数: 0.903) (未发表数据); 但若先将样地分割为500个20 m × 20 m的样方再进行对比, 各样方内常绿种的多样性则要显著地高于落叶种(Wilcox检验, P < 0.001)。
1.4 物种多度分布的表示
图示法可以简单直观地表示物种的多度分布。通常情况下, 表示方法主要有3种, 分别是: 直方图法(histogram plot)、多度等级分布(rank abundance distribution, RAD)以及累积经验分布函数(empirical cumulative distribution function, ECDF) (McGill, 2010 )。使用直方图法表示物种多度分布时, 需要将物种个体数进行分组, 然而不同的分组方式会影响到图形的表示以及对它的解释(Gray et al, 2006 )。RAD由Whittaker (1965)提出, 作图时x轴表示多度的等级, y轴一般为对数化后的多度。该方法表示的物种多度分布易于解释, 但依然存在两方面的问题, 即进行数学处理时存在困难以及不同的RAD之间不易比较(McGill, 2010 )。由于ECDF能够克服RAD的上述缺点, 尤其是能够很好地体现群落间SAD的差异(Matthews & Whittaker, 2015 ), 因而受到了生态学家的推荐(McGill, 2010 )。本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较。
1.5 模型的选择
本文选择了6种模型对常绿与落叶物种的物种多度数据进行拟合, 分别为: 对数正态模型、对数级数模型、断棍模型、生态位优先占领模型(niche preemption model)、复合群落零和多项式模型(metacommunity zero-sum multinomial distribution model, MZD model)以及Volkov模型(Volkov model)。其中前2个模型为纯统计模型, 中间2个为生态位模型, 最后2个属于中性理论模型的范畴。
1.5.1 纯统计模型
(1)对数正态模型。最早由Preston (1948)将其引入到对物种多度分布的研究当中。该模型假设群落内物种个体数的对数符合正态分布, 即对数正态分布。若将第i 个物种的多度记作A i , 则有:
( i = 1, 2, 3,…, S ) (1)
式中, μ 和δ 分别表示正态分布的均值和方差, Φ 为正态偏差。
(2)对数级数模型。对数级数分布是负二项分布在k = 0时的特殊情况, 该模型不考虑没有个体存在的种(Fisher et al, 1943 ; 刘灿然等, 1995 )。根据本模型, 群落内多度为n 的物种数S 可表示为:
(2)
式中, α 代表群落的物种多样性, 类似于物种丰富度的概念(McGill, 2010 ); X 为常数(0 < X ≤ 1), 与群落的大小有关(张姗等, 2015 )。
1.5.2 生态位模型
(1)断棍模型。该模型假设某一群落内的总生态位是长度为1的一条短棍, 若将其分割为S 段, 则代表生态位被S 个物种所占有(MacArthur, 1957 ; 程佳佳等, 2011 )。模型假定S 个物种的分类地位和竞争能力均相似, 且在群落中同时出现(程佳佳等, 2011 ; 张姗等, 2015 )。若以J 表示群落内物种的个体总数, 则可将第i 个种的多度A i 表示为:
( i = 1, 2, 3,…, S ) (3)
(2)生态位优先占领模型。模型假定种1先占用群落总生态位的k 份, 种2占用剩下的k (1-k )份, 种3再继续占据余下的k (1-k )2 份, 依次类推, 直至剩余资源无法继续维持另一个物种的生存(Motonura, 1932 ; 程佳佳等, 2011 ; 张姗等, 2015 )。本模型中第i 个物种的多度A i 可表示为:
( i = 1, 2, 3,…, S ) (4)
1.5.3 中性理论模型
(1)复合群落零和多项式模型。该模型假定某一样点的物种多度分布来自于中性复合群落的随机漂变(Alonso & McKane, 2004 )。模型中包括了两个参数: 取样点内的个体数(J )和基本生物多样性指数(fundamental biodiversity number, θ ), 对数级数分布就是本模型的一个特例(Hubbell, 2001 ), 因此两者的拟合效果非常相似。根据该模型, 复合群落内任一取样点内多度为n 的物种数S 可表达为:
(5)
(6)
(2) Volkov模型。该模型在拟合群落的物种多度分布时, 相较于复合群落零和多项式模型增加了迁移系数(immigration rate, m ) (Volkov et al, 2003 ), 并假定此迁移系数在物种从复合群落到局域群落的过程中是不变的(张姗等, 2015 )。根据本模型, 局域群落内多度为n 的物种数S 可表示为:
(7)
(8)
(9)
式中, γ 表示迁移到局域群落内的个体数(Volkov et al, 2003 ; 张姗等, 2015 )。
1.6 模型拟合效果检验
本研究使用K-S检验对模型的拟合效果进行验证。K-S检验是一种非参数检验的方法, 它通过计算两个样本经验分布函数(empirical distribution function)之间的距离(统计量D )来判断二者是否存在显著差异。为了避免应用该检验方法时出现数据连结的问题, 特别选用了基于bootstrap模拟方法的K-S检验(Sekhon, 2008 ), bootstrap的次数为1,000次。当P < 0.05时, 表明该模型被拒绝。
同时, 我们还利用赤池信息准则(Akaike information criterion, AIC)来比较模型拟合的优劣。AIC的优点在于其强调模型预测最优性的同时, 也兼顾了模型的简约性。一般而言, AIC数值越小, 表明拟合效果越好。
数据处理过程均基于R-3.2.0 软件(R Core Team, 2012 )。其中, 模型拟合使用sads软件包完成; 基于bootstrap的K-S检验利用Matching软件包完成。
2 结果
2.1 常绿与落叶物种的多度分布
由样地内常绿与落叶物种的累积经验分布可知(图1 ), 两者的ECDF均呈现出一定程度的S型。虽然从图1 中能够看出, 落叶物种相较于常绿物种有着更高的稀有种比例, 但结合K-S检验结果发现, 两类生活型的ECDF之间并无显著差异(D = 0.210, P = 0.142)。
图1 天童20 ha常绿阔叶林样地内常绿与落叶物种的累积经验分布函数。虚线与实线均为局部加权多项式的拟合线。
Fig. 1 The empirical cumulative distribution function of evergreen and deciduous woody plants in Tiantong 20 ha evergreen broad-leaved forest plot. The dashed and solid lines are fitted by local polynomial regression (LOESS).
2.2 常绿与落叶物种多度分布曲线的拟合
根据K-S检验结果, 除生态位模型中的断棍模型外(P < 0.001), 其余5个模型对常绿与落叶物种的物种-多度分布曲线的拟合均可被接受(表1 )。另外, 经由AIC值判断, 这5个模型对于两类生活型物种多度分布的拟合优度排序一致, 依次为: Volkov模型>复合群落零和多项式模型>对数级数模型>对数正态模型>生态位优先占领模型(表1 )。无论是对于常绿还是落叶物种而言, 对其物种多度分布拟合效果较好的前3个模型之间的差别都非常小(AIC值之间的差值最大为1.322) (表1 )。进一步结合图2 中的拟合结果可知, 两个中性理论模型(具体参数见表2 )以及两个统计模型都能够较好地拟合常绿与落叶物种的物种多度分布, 而生态位模型的拟合效果则较为一般。两个中性模型的参数均显示, 相较于常绿物种, 落叶物种有着更高的基本多样性指数和迁移系数(表2 )。
图2 天童20 ha常绿阔叶林样地内常绿与落叶物种的物种多度分布及模型拟合。观测值用空心点表示。
Fig. 2 The species-abundance distribution and model fitting for evergreen and deciduous woody plants in Tiantong 20 ha evergreen broad-leaved forest plot. Observed values are shown as open circles. MZD model, metacommunity zero-sum multinomial distribution model.
3 讨论
通过对天童常绿阔叶林样地内常绿与落叶物种的物种多度分布格局进行对比和分析, 我们发现: 虽然样地内的常绿与落叶物种在物种多样性和重要值方面都存在不同程度的差异(杨庆松等, 2011 ), 但从物种多度分布的角度来看(图1 ), 两者却没有显著区别, 而且其最优拟合模型同为中性理论模型(表1 , 图2 )。据此可推知, 尽管这两类物种在天童常绿阔叶林群落中的地位与作用差别很大, 但主导其各自物种多度分布格局形成的生态学过程可能是类似的。
天童样地内的79个落叶物种中, 稀有种的比例达46.8%, 而常绿物种中的稀有种只占到其总物种数的24.7%。此外两者在总多度方面也有着十分明显的差异。因此, 为何数量特征差别如此明显的两类物种却有着相近的物种多度分布, 就成了我们所关注的问题。自然界中, 物种组成差异明显但其多度分布却近似相同的情况并不鲜见。例如, 张姗等(2015)在对长白山阔叶红松林25 ha固定监测样地中草本植物多度分布的研究中发现, 虽然随着季节变化, 样地内林下草本层中的植物在组成和数量上有较大差异, 但是不同季节草本层物种多度分布的模型拟合结果却是相似的, 在一定程度上证明不同季节的草本植物群落也可能有着类似的多样性维持机制。McEwan和Muller (2011)在研究美国东北部温带森林林下草本植物多样性的季节变化时亦发现, 同一森林群落内草本植物的多样性格局并未随季节发生明显改变: 在3次调查中(4月、6月和8月), 草本层盖度的最大值均主要出现在海拔较低的阴坡位置; 林下草本植物群落的多样性指标(物种丰富度和均匀度等)在不同季节里也没有显著差异。他们猜测这种情况可能是由于群落发展到顶极阶段后, 草本植物的数量已接近其最大容纳量(maximum species packing), 从而使得草本植物虽然在种类组成上具有季节性, 却有着相近的维持机制(McEwan & Muller, 2011 )。天童样地内的森林为成熟的常绿阔叶林, 因此无论是在当中占据绝对优势的常绿物种, 还是通常以斑块形式存在于其内的落叶物种, 同种生活型内的物种在数量比例等方面可能均已经相对稳定, 所以即使两者在某些多样性指标等方面有所差异, 也并不一定意味着其维持机制必然 不同。
此外, 生态学家们已经发现, 将具有不同生态特性(如个体大小、扩散能力等)的物种合并考虑时, 可能会造成某些格局(如物种多度分布)潜在的特殊性被掩盖(Matthews et al, 2014 ; Matthews & Whittaker, 2015 )。例如, Magurran和Henderson (2003)发现, 群落整体的物种多度分布格局是其中持久种(persistent species)或核心种(core species)与机会种(occasional species)多度分布的综合体现。所谓持久种(或核心种)是指个体多度较高且在区域内长期存在的物种, 而机会种则不一定在每次调查时都会出现且其多度一般较低(Magurran & Henderson, 2003 )。Magurran和Henderson (2003)将在英国西部一河口地区调查到的鱼类划分为持久种与机会种后, 对它们的物种多度分布进行了分析, 结果显示, 前者表现为对数正态分布, 而后者则呈现出对数级数分布的特点; 但若不进行这类细分, 而是将所有鱼类物种一并考虑的话, 这时的物种多度分布会表现为一种负偏态(negative skew)的形式。虽然本研究中将常绿与落叶物种的物种多度分布进行了独立分析, 但在两种生活型内部, 也必然存在种间的差异, 特别是在物种多度方面的差别。从多度排序上看, 常绿物种中前20位物种的多度之和便已占到其总多度的90.5%; 落叶物种中前26位物种的多度之和也占到落叶物种总多度的近90%, 这说明两者也存在由少数物种在群落中占据较大优势的情况。因而, 根据Magurran和Henderson (2003)的研究结论, 在将生活型内的物种进行混合考虑时, 由于不同的多度分布之间相互重叠, 确实可能造成某些信息的丢失, 从而得出两者物种多度分布格局差异不明显的结论。若要验证并克服这一问题, 则需要在今后的研究中对两种生活型内的物种进行更为细致的划分与分析。
生态位模型中的断棍模型无法通过K-S检验, 生态位优先占领模型虽然能够通过K-S检验, 但根据其AIC值可知, 它的拟合效果相比于另外几个模型较为一般。谢玉彬等(2012)使用CCA排序的方法分析了天童常绿阔叶林样地内常绿和落叶物种与3类地形因子(海拔、坡度、地形凸度)之间的关系。他们发现地形因子只能解释两者物种组成变异的19.2% (常绿物种)和7% (落叶物种)。这表明至少在地形这一维度上, 生态位理论并不能很好地解释二者各自的多度分布格局, 从而在一定程度上支持了本文的研究结论。此外, 在演替顶极阶段的群落内, 无论是物种组成还是数量比例等都已较为稳定, 种间竞争等生态位过程往往并不明显(闫琰等, 2012 ; 张姗等, 2015 ), 而且同一功能群内部(如常绿或落叶生活型)的各物种之间在生态习性上的差距也相对较小(Siepielski et al, 2010 ; Matthews & Whittaker, 2014 ), 这都有可能会降低生态位过程在常绿与落叶物种多度格局形成过程中的重要性。
相对地, 两个中性理论模型均能够较好地对天童常绿阔叶林内常绿和落叶木本植物的物种多度分布进行拟合, 这说明相对于生态位过程, 中性过程在两者物种多度分布形成中的作用可能更大。已有研究表明, 生态位格局与中性格局并非是两种相互排斥的群落物种多样性格局, 它们更像是一种连续格局中的两个“端点”, 在两者之间存在着一个逐渐过渡的阶段(Fisher & Mehta, 2014 )。也就是说, 任意群落或许都能够在“纯生态位结构到纯中性结构连续体” (niche-neutrality continuum)上找到自己对应的位置, 例如, 中性群落即可被认为是该连续体上当种间适应性无差异, 且不存在稳定的生态位分化时的特例(Bar-Massada et al, 2014 ; Matthews & Whittaker, 2014 )。因而, 我们推测生态位过程和中性过程在决定群落物种组成中所起的作用可能是此消彼长的, 即当生态位过程的影响下降时, 可能相应地伴随着中性过程作用的增强。
在对物种多度分布的拟合效果方面, 之前的研究中经常提到中性理论模型在某些条件下相对于生态位模型具有优势。例如, 中性理论模型在大尺度物种多度格局的拟合方面往往表现较好(程佳佳等, 2011 ; 闫琰等, 2012 ; Cheng et al, 2012 ; Fisher & Mehta, 2014 ), 而且其对物种多样性较高的群落中的物种多度分布拟合也较生态位模型更好(Chisholm & Pacala, 2010 )。根据前述的“生态位-中性连续体”概念可推知, 这些结论或许是从不同的侧面反映出当研究对象具备了上述的特点时, 便可能造成生态位过程和中性过程在群落物种多度分布格局形成中的相对重要性发生变化。
常绿与落叶物种作为两类有着不同物候性状与生长策略的物种集合, 在功能性状上也有着多方面的不同。例如, 相较于常绿物种而言, 落叶物种的比叶面积(specific leaf area, SLA)往往较大, 且其叶片中水分以及氮磷元素的含量也更高(Bai et al, 2015 )。一般而言, 不同的功能性状对于不同的生态学过程(如生态位过程和中性过程等)可能有着完全相反的响应(Cornwell & Ackerly, 2010 ; 房帅等, 2014 )。因此, 尽管我们在探讨天童样地内常绿与落叶物种时, 发现两者多度分布的最优拟合模型相同, 但当我们考虑样地内植物的其他功能性状时, 则有可能得到不同的结果。
生态学研究中, 格局和过程之间往往不是一一对应的关系, 因此由格局反推其形成机制的做法存在一定的局限性(Alonso et al, 2008 ; 张姗等, 2015 )。就物种多度格局而言, 对它的分析和理解有助于人们深入认识群落多样性的构建机制, 然而在这过程中它仅是一个必要非充分条件(McGill et al, 2007 )。实践中, 多个机理完全不同的模型在拟合同一组数据时, 其效果可能都较好, 所以单纯基于物种多度格局的模型拟合结果, 并无法充分验证其背后的生态学机制(Volkov et al, 2003 ; Magurran, 2005 )。因而, 基于本文的分析, 我们只能初步认为在天童常绿阔叶林中, 中性过程对常绿和落叶物种多样性格局的形成可能起着更为重要的作用, 而它相对于其他生态学机制(如生态位过程等)的贡献, 则需要结合一系列环境因子、生物因子甚至空间因子进行更为深入的分析(张姗等, 2015 )。
参考文献
文献选项
[1]
Alonso D McKane AJ 2004 ) Sampling Hubbell’s neutral model of biodiversity.
Ecology Letters , 7 , 901 -910 .
[本文引用: 1]
[2]
Alonso D Ostling A Etienne RS 2008 ) The implicit assumption of symmetry and the species abundance distribution.
Ecology Letters , 11 , 93 -105 .
[本文引用: 2]
[3]
Bai K He C Wan X Jiang D 2015 ) Leaf economics of evergreen and deciduous tree species along an elevational gradient in a subtropical mountain. AoB Plants, 7, plv064.
[本文引用: 1]
[4]
Bar-Massada A Kent R Carmel Y 2014 ) Environmental heterogeneity affects the location of modelled communities along the niche-neutrality continuum.
Proceedings of the Royal Society of London B: Biological Sciences , 281 , 20133249 .
[本文引用: 1]
[5]
Borda-de-Água L Borges Paulo AV Hubbell SP Pereira HM 2012 ) Spatial scaling of species abundance distributions.
Ecography , 35 , 549 -556 .
[本文引用: 1]
[6]
Cheng JJ Mi XC Ma KP Zhang JT 2011 ) Responses of species-abundance distribution to varying sampling scales in a subtropical broad-leaved forest.
Biodiversity Science , 19 , 168 -177 . (in Chinese with English abstract)
[程佳佳 , 米湘成 , 马克平 , 张金屯 (2011 ) 亚热带常绿阔叶林群落物种多度分布格局对取样尺度的响应
. 生物多样性 , 19 , 168 -177 .]
[7]
Cheng JJ Mi XC Nadrowski K Ren HB Zhang JT Ma KP 2012 ) Separating the effect of mechanisms shaping species-abundance distributions at multiple scales in a subtropical forest.
Oikos , 121 , 236 -244 .
[本文引用: 5]
[8]
Chisholm RA Pacala SW 2010 ) Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proceedings of the National Academy of Sciences,
USA , 107 , 15821 -15825 .
[本文引用: 1]
[9]
Cornwell WK Ackerly DD 2010 ) A link between plant traits and abundance: evidence from coastal California woody plants.
Journal of Ecology , 98 , 814 -821 .
[本文引用: 1]
[10]
Fang S Yuan ZQ Lin F Ye J Hao ZQ Wang XG 2014 ) Functional and phylogenetic structures of woody plants in broad-leaved Korean pine mixed forest in Changbai Mountains, Jilin, China.
Chinese Science Bulletin , 59 , 2342 -2348 . (in Chinese with English abstract)
[本文引用: 1]
[房帅 , 原作强 , 蔺菲 , 叶吉 , 郝占庆 , 王绪高 (2014 ) 长白山阔叶红松林木本植物系统发育与功能性状结构
. 科学通报 , 59 , 2342 -2348 .]
[本文引用: 1]
[11]
Fisher CK Mehta P 2014 ) The transition between the niche and neutral regimes in ecology. Proceedings of the National Academy of Sciences,
USA , 111 , 13111 -13116 .
[12]
Fisher RA Corbet AS Williams CB 1943 ) The relation between the number of species and the number of individuals in a random sample of an animal population.
Journal of Animal Ecology , 12 , 42 -58 .
[本文引用: 1]
[13]
Gray JS Bjørgesæter A Ugland KI 2006 ) On plotting species abundance distributions.
Journal of Animal Ecology , 75 , 752 -756 .
[本文引用: 2]
[14]
Hubbell SP 2001 ) The Unified Neutral Theory of Biodiversity and Biogeography . Princeton University Press, Princeton , New Jersey .
[本文引用: 2]
[15]
Liu CR Ma KP Zhou WN 1995 ) Measurement of biotic community diversity. III. Statistical issue related to species- abundance distribution.
Chinese Biodiversity , 3 , 157 -169 . (in Chinese)
[本文引用: 1]
[刘灿然 , 马克平 , 周文能 (1995 ) 生物群落多样性的测度方法.III. 与物种-多度分布模型有关的统计问题
. 生物多样性 , 3 , 157 -169 .]
[本文引用: 1]
[16]
Ma KM 2003 ) Advances of the study on species abundance pattern.
Acta Phytoecologica Sinica , 27 , 412 -426 . (in Chinese with English abstract)
[本文引用: 2]
[马克明 (2003 ) 物种多度格局研究进展
. 植物生态学报 , 27 , 412 -426 .]
[本文引用: 2]
[17]
MacArthur RH 1957 ) On the relative abundance of bird species. Proceedings of the National Academy of Sciences,
USA , 43 , 293 -295 .
[18]
Magurran AE 2005 ) Species abundance distributions: pattern or process?
Functional Ecology , 19 , 177 -181 .
[本文引用: 1]
[19]
Magurran AE Henderson PA 2003 ) Explaining the excess of rare species in natural species abundance distributions.
Nature , 422 , 714 -716 .
[20]
Matthews TJ Borges Paulo AV Whittaker RJ 2014 ) Multimodal species abundance distributions: a deconstruction approach reveals the processes behind the pattern.
Oikos , 123 , 533 -544 .
[21]
Matthews TJ Whittaker RJ 2014 ) Neutral theory and the species abundance distribution: recent developments and prospects for unifying niche and neutral perspectives.
Ecology and Evolution , 4 , 2263 -2277 .
[本文引用: 1]
[22]
Matthews TJ Whittaker RJ 2015 ) On the species abundance distribution in applied ecology and biodiversity management.
Journal of Applied Ecology , 52 , 443 -454 .
[本文引用: 1]
[23]
McEwan R Muller R 2011 ) Dynamics, diversity, and resource gradient relationships in the herbaceous layer of an old-growth Appalachian forest.
Plant Ecology , 212 , 1179 -1191 .
[本文引用: 1]
[24]
McGill BJ Etienne RS Gray JS Alonso D Anderson MJ Benecha HK Dornelas M Enquist BJ Green JL He FL Hurlbert AH Magurran AE Marquet PA Maurer BA Ostling A Soykan CU Ugland KI White EP 2007 ) Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework.
Ecology Letters , 10 , 995 -1015 .
[本文引用: 1]
[25]
McGill BJ 2010 ) Species abundance distributions. In: Biological Diversity: Frontiers in Measurement and Assessment (eds Magurran AE, McGill BJ) . Oxford University Press , New York .
[本文引用: 3]
[26]
Motonura I 1932 ) On the statistical treatment of communities.
Zoological Magazine (Tokyo) , 44 , 379 -383 .
[本文引用: 3]
[27]
Preston FW 1948 ) The commonness, and rarity, of species.
Ecology , 29 , 254 -283 .
[本文引用: 1]
[28]
R Core Team 2012 ) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.
[本文引用: 6]
[29]
Sekhon JS 2008 ) Multivariate and propensity score matching software with automated balance optimization: the matching package for R.
Journal of Statistical Software , 42 , 1 -52 .
[本文引用: 6]
[30]
Siepielski AM Hung KL Bein Eben EB McPeek MA 2010 ) Experimental evidence for neutral community dynamics governing an insect assemblage.
Ecology , 91 , 847 -857 .
[本文引用: 1]
[31]
Song YC 1988 ) The essential characteristics and main types of the broad-leaved evergreen forest in China.
Phytocoenologia , 16 , 105 -123 .
[本文引用: 1]
[32]
Song YC Wang XR 1995 ) Vegetation and Flora of Tiantong National Forest Park, Zheijiang Province, China . Shanghai Sciencific and Technological Literature Press , Shanghai . (in Chinese)
[本文引用: 1]
[宋永昌 , 王祥荣 (1995 ) 浙江天童国家森林公园的植被和区系. 上海科学技术文献出版社 , 上海 .]
[本文引用: 1]
[33]
Song YC Yan ER Song K 2015 ) Synthetic comparison of eight dynamics plots in evergreen broadleaf forest, China.
Biodiversity Science , 23 , 139 -148 . (in Chinese with English abstract)
[本文引用: 1]
[宋永昌 , 阎恩荣 , 宋坤 (2015 ) 中国常绿阔叶林8大动态监测样地植被的综合比较
. 生物多样性 , 23 , 139 -148 .]
[本文引用: 1]
[34]
Ulrich W Ollik M Ugland KI 2010 ) A meta-analysis of species-abundance distributions.
Oikos , 119 , 1149 -1155 .
[本文引用: 1]
[35]
Volkov I Banavar JR Hubbell SP Maritan A 2003 ) Neutral theory and relative species abundance in ecology.
Nature , 424 , 1035 -1037 .
[本文引用: 1]
[36]
Wang XH Kent M Fang XF 2007 ) Evergreen broad-leaved forest in Eastern China: its ecology and conservation and the importance of resprouting in forest restoration.
Forest Ecology and Management , 245 , 76 -87 .
[37]
White EP Thibault KM Xiao X 2012 ) Characterizing species abundance distributions across taxa and ecosystems using a simple maximum entropy model.
Ecology , 93 , 1772 -1778 .
[本文引用: 3]
[38]
Whittaker RH 1965 ) Dominance and diversity in land plant communities: numerical relations of species express the importance of competition in community function and evolution.
Science , 147 , 250 -260 .
[39]
Xie YB Ma ZP Yang QS Fang XF Zhang ZG Yan ER Wang XH 2012 ) Coexistence mechanisms of evergreen and deciduous trees based on topographic factors in Tiantong region, Zhejiang Province, eastern China.
Biodiversity Science , 20 , 159 -167 . (in Chinese with English abstract)
[本文引用: 1]
[谢玉彬 , 马遵平 , 杨庆松 , 方晓峰 , 张志国 , 阎恩荣 , 王希华 (2012 ) 基于地形因子的天童地区常绿树种和落叶树种共存机制研究
. 生物多样性 , 20 , 159 -167 .]
[本文引用: 1]
[40]
Yan Y Zhang CY Zhao XH 2012 ) Species-abundance distribution patterns at different successional stages of conifer and broad-leaved mixed forest communities in Changbai Mountains, China.
Chinese Journal of Plant Ecology , 36 , 923 -934 . (in Chinese with English abstract)
[本文引用: 1]
[闫琰 , 张春雨 , 赵秀海 (2012 ) 长白山不同演替阶段针阔混交林群落物种多度分布格局
. 植物生态学报 , 36 , 923 -934 .]
[本文引用: 1]
[41]
Yang QS Ma ZP Xie YB Zhang ZG Wang ZH Liu HM Li P Zhang N Wang DL Yang HB Fang XF Yan ER Wang XH 2011 ) Community structure and species composition of an evergreen broad-leaved forest in Tiantong’s 20 ha dynamic plot, Zhejiang Province, eastern China.
Biodiversity Science , 19 , 215 -223 . (in Chinese with English abstract)
[本文引用: 3]
[杨庆松 , 马遵平 , 谢玉彬 , 张志国 , 王樟华 , 刘何铭 , 李萍 , 张娜 , 王达力 , 杨海波 , 方晓峰 , 阎恩荣 , 王希华 (2011 ) 浙江天童20 ha常绿阔叶林动态监测样地的群落特征
. 生物多样性 , 19 , 215 -223 .]
[本文引用: 3]
[42]
Zhang S Lin F Yuan ZQ Kuang X Jia SH Wang YY Suo YY Fang S Wang XG Ye J Hao ZQ 2015 ) Herb layer species abundance distribution patterns in different seasons in an old-growth temperate forest in Changbai Mountain, China.
Biodiversity Science , 23 , 641 -648 . (in Chinese with English abstract)
[本文引用: 1]
[张姗 , 蔺菲 , 原作强 , 匡旭 , 贾仕宏 , 王芸芸 , 索炎炎 , 房帅 , 王绪高 , 叶吉 , 郝占庆 (2015 ) 长白山阔叶红松林草本层物种多度分布格局及其季节动态
. 生物多样性 , 23 , 641 -648 .]
[本文引用: 1]
Sampling Hubbell’s neutral model of biodiversity.
1
2004
... (1)复合群落零和多项式模型.该模型假定某一样点的物种多度分布来自于中性复合群落的随机漂变(Alonso & McKane, 2004 ).模型中包括了两个参数: 取样点内的个体数(J )和基本生物多样性指数(fundamental biodiversity number, θ ), 对数级数分布就是本模型的一个特例(Hubbell, 2001 ), 因此两者的拟合效果非常相似.根据该模型, 复合群落内任一取样点内多度为n 的物种数S 可表达为: ...
The implicit assumption of symmetry and the species abundance distribution.
2
2008
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... 生态学研究中, 格局和过程之间往往不是一一对应的关系, 因此由格局反推其形成机制的做法存在一定的局限性(Alonso et al, 2008 ; 张姗等, 2015 ).就物种多度格局而言, 对它的分析和理解有助于人们深入认识群落多样性的构建机制, 然而在这过程中它仅是一个必要非充分条件(McGill et al, 2007 ).实践中, 多个机理完全不同的模型在拟合同一组数据时, 其效果可能都较好, 所以单纯基于物种多度格局的模型拟合结果, 并无法充分验证其背后的生态学机制(Volkov et al, 2003 ; Magurran, 2005 ).因而, 基于本文的分析, 我们只能初步认为在天童常绿阔叶林中, 中性过程对常绿和落叶物种多样性格局的形成可能起着更为重要的作用, 而它相对于其他生态学机制(如生态位过程等)的贡献, 则需要结合一系列环境因子、生物因子甚至空间因子进行更为深入的分析(张姗等, 2015 ). ...
Leaf economics of evergreen and deciduous tree species along an elevational gradient in a subtropical mountain. AoB Plants, 7, plv064.
1
2015
... 常绿与落叶物种作为两类有着不同物候性状与生长策略的物种集合, 在功能性状上也有着多方面的不同.例如, 相较于常绿物种而言, 落叶物种的比叶面积(specific leaf area, SLA)往往较大, 且其叶片中水分以及氮磷元素的含量也更高(Bai et al, 2015 ).一般而言, 不同的功能性状对于不同的生态学过程(如生态位过程和中性过程等)可能有着完全相反的响应(Cornwell & Ackerly, 2010 ; 房帅等, 2014 ).因此, 尽管我们在探讨天童样地内常绿与落叶物种时, 发现两者多度分布的最优拟合模型相同, 但当我们考虑样地内植物的其他功能性状时, 则有可能得到不同的结果. ...
Environmental heterogeneity affects the location of modelled communities along the niche-neutrality continuum.
1
2014
... 相对地, 两个中性理论模型均能够较好地对天童常绿阔叶林内常绿和落叶木本植物的物种多度分布进行拟合, 这说明相对于生态位过程, 中性过程在两者物种多度分布形成中的作用可能更大.已有研究表明, 生态位格局与中性格局并非是两种相互排斥的群落物种多样性格局, 它们更像是一种连续格局中的两个“端点”, 在两者之间存在着一个逐渐过渡的阶段(Fisher & Mehta, 2014 ).也就是说, 任意群落或许都能够在“纯生态位结构到纯中性结构连续体” (niche-neutrality continuum)上找到自己对应的位置, 例如, 中性群落即可被认为是该连续体上当种间适应性无差异, 且不存在稳定的生态位分化时的特例(Bar-Massada et al, 2014 ; Matthews & Whittaker, 2014 ).因而, 我们推测生态位过程和中性过程在决定群落物种组成中所起的作用可能是此消彼长的, 即当生态位过程的影响下降时, 可能相应地伴随着中性过程作用的增强. ...
Spatial scaling of species abundance distributions.
1
2012
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
亚热带常绿阔叶林群落物种多度分布格局对取样尺度的响应
2011
亚热带常绿阔叶林群落物种多度分布格局对取样尺度的响应
2011
Separating the effect of mechanisms shaping species-abundance distributions at multiple scales in a subtropical forest.
5
2012
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... (1)断棍模型.该模型假设某一群落内的总生态位是长度为1的一条短棍, 若将其分割为S 段, 则代表生态位被S 个物种所占有(MacArthur, 1957 ; 程佳佳等, 2011 ).模型假定S 个物种的分类地位和竞争能力均相似, 且在群落中同时出现(程佳佳等, 2011 ; 张姗等, 2015 ).若以J 表示群落内物种的个体总数, 则可将第i 个种的多度A i 表示为: ...
... 个物种的分类地位和竞争能力均相似, 且在群落中同时出现(程佳佳等, 2011 ; 张姗等, 2015 ).若以J 表示群落内物种的个体总数, 则可将第i 个种的多度A i 表示为: ...
... (2)生态位优先占领模型.模型假定种1先占用群落总生态位的k 份, 种2占用剩下的k (1-k )份, 种3再继续占据余下的k (1-k )2 份, 依次类推, 直至剩余资源无法继续维持另一个物种的生存(Motonura, 1932 ; 程佳佳等, 2011 ; 张姗等, 2015 ).本模型中第i 个物种的多度A i 可表示为: ...
... 在对物种多度分布的拟合效果方面, 之前的研究中经常提到中性理论模型在某些条件下相对于生态位模型具有优势.例如, 中性理论模型在大尺度物种多度格局的拟合方面往往表现较好(程佳佳等, 2011 ; 闫琰等, 2012 ; Cheng et al, 2012 ; Fisher & Mehta, 2014 ), 而且其对物种多样性较高的群落中的物种多度分布拟合也较生态位模型更好(Chisholm & Pacala, 2010 ).根据前述的“生态位-中性连续体”概念可推知, 这些结论或许是从不同的侧面反映出当研究对象具备了上述的特点时, 便可能造成生态位过程和中性过程在群落物种多度分布格局形成中的相对重要性发生变化.
Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proceedings of the National Academy of Sciences,
1
2010
... 在对物种多度分布的拟合效果方面, 之前的研究中经常提到中性理论模型在某些条件下相对于生态位模型具有优势.例如, 中性理论模型在大尺度物种多度格局的拟合方面往往表现较好(程佳佳等, 2011 ; 闫琰等, 2012 ; Cheng et al, 2012 ; Fisher & Mehta, 2014 ), 而且其对物种多样性较高的群落中的物种多度分布拟合也较生态位模型更好(Chisholm & Pacala, 2010 ).根据前述的“生态位-中性连续体”概念可推知, 这些结论或许是从不同的侧面反映出当研究对象具备了上述的特点时, 便可能造成生态位过程和中性过程在群落物种多度分布格局形成中的相对重要性发生变化.
A link between plant traits and abundance: evidence from coastal California woody plants.
1
2010
... 在对物种多度分布的拟合效果方面, 之前的研究中经常提到中性理论模型在某些条件下相对于生态位模型具有优势.例如, 中性理论模型在大尺度物种多度格局的拟合方面往往表现较好(程佳佳等, 2011 ; 闫琰等, 2012 ; Cheng et al, 2012 ; Fisher & Mehta, 2014 ), 而且其对物种多样性较高的群落中的物种多度分布拟合也较生态位模型更好(Chisholm & Pacala, 2010 ).根据前述的“生态位-中性连续体”概念可推知, 这些结论或许是从不同的侧面反映出当研究对象具备了上述的特点时, 便可能造成生态位过程和中性过程在群落物种多度分布格局形成中的相对重要性发生变化.
长白山阔叶红松林木本植物系统发育与功能性状结构
1
2014
... 常绿与落叶物种作为两类有着不同物候性状与生长策略的物种集合, 在功能性状上也有着多方面的不同.例如, 相较于常绿物种而言, 落叶物种的比叶面积(specific leaf area, SLA)往往较大, 且其叶片中水分以及氮磷元素的含量也更高(Bai et al, 2015 ).一般而言, 不同的功能性状对于不同的生态学过程(如生态位过程和中性过程等)可能有着完全相反的响应(Cornwell & Ackerly, 2010 ; 房帅等, 2014 ).因此, 尽管我们在探讨天童样地内常绿与落叶物种时, 发现两者多度分布的最优拟合模型相同, 但当我们考虑样地内植物的其他功能性状时, 则有可能得到不同的结果. ...
长白山阔叶红松林木本植物系统发育与功能性状结构
1
2014
... 常绿与落叶物种作为两类有着不同物候性状与生长策略的物种集合, 在功能性状上也有着多方面的不同.例如, 相较于常绿物种而言, 落叶物种的比叶面积(specific leaf area, SLA)往往较大, 且其叶片中水分以及氮磷元素的含量也更高(Bai et al, 2015 ).一般而言, 不同的功能性状对于不同的生态学过程(如生态位过程和中性过程等)可能有着完全相反的响应(Cornwell & Ackerly, 2010 ; 房帅等, 2014 ).因此, 尽管我们在探讨天童样地内常绿与落叶物种时, 发现两者多度分布的最优拟合模型相同, 但当我们考虑样地内植物的其他功能性状时, 则有可能得到不同的结果. ...
The transition between the niche and neutral regimes in ecology. Proceedings of the National Academy of Sciences,
2014
The relation between the number of species and the number of individuals in a random sample of an animal population.
1
1943
... 常绿与落叶物种作为两类有着不同物候性状与生长策略的物种集合, 在功能性状上也有着多方面的不同.例如, 相较于常绿物种而言, 落叶物种的比叶面积(specific leaf area, SLA)往往较大, 且其叶片中水分以及氮磷元素的含量也更高(Bai et al, 2015 ).一般而言, 不同的功能性状对于不同的生态学过程(如生态位过程和中性过程等)可能有着完全相反的响应(Cornwell & Ackerly, 2010 ; 房帅等, 2014 ).因此, 尽管我们在探讨天童样地内常绿与落叶物种时, 发现两者多度分布的最优拟合模型相同, 但当我们考虑样地内植物的其他功能性状时, 则有可能得到不同的结果. ...
On plotting species abundance distributions.
2
2006
... 相对地, 两个中性理论模型均能够较好地对天童常绿阔叶林内常绿和落叶木本植物的物种多度分布进行拟合, 这说明相对于生态位过程, 中性过程在两者物种多度分布形成中的作用可能更大.已有研究表明, 生态位格局与中性格局并非是两种相互排斥的群落物种多样性格局, 它们更像是一种连续格局中的两个“端点”, 在两者之间存在着一个逐渐过渡的阶段(Fisher & Mehta, 2014 ).也就是说, 任意群落或许都能够在“纯生态位结构到纯中性结构连续体” (niche-neutrality continuum)上找到自己对应的位置, 例如, 中性群落即可被认为是该连续体上当种间适应性无差异, 且不存在稳定的生态位分化时的特例(Bar-Massada et al, 2014 ; Matthews & Whittaker, 2014 ).因而, 我们推测生态位过程和中性过程在决定群落物种组成中所起的作用可能是此消彼长的, 即当生态位过程的影响下降时, 可能相应地伴随着中性过程作用的增强. ...
... 在对物种多度分布的拟合效果方面, 之前的研究中经常提到中性理论模型在某些条件下相对于生态位模型具有优势.例如, 中性理论模型在大尺度物种多度格局的拟合方面往往表现较好(程佳佳等, 2011 ; 闫琰等, 2012 ; Cheng et al, 2012 ; Fisher & Mehta, 2014 ), 而且其对物种多样性较高的群落中的物种多度分布拟合也较生态位模型更好(Chisholm & Pacala, 2010 ).根据前述的“生态位-中性连续体”概念可推知, 这些结论或许是从不同的侧面反映出当研究对象具备了上述的特点时, 便可能造成生态位过程和中性过程在群落物种多度分布格局形成中的相对重要性发生变化.
2
2001
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... (2)对数级数模型.对数级数分布是负二项分布在k = 0时的特殊情况, 该模型不考虑没有个体存在的种(Fisher et al, 1943 ; 刘灿然等, 1995 ).根据本模型, 群落内多度为n 的物种数S 可表示为: ...
生物群落多样性的测度方法.III. 与物种-多度分布模型有关的统计问题
1
1995
... 图示法可以简单直观地表示物种的多度分布.通常情况下, 表示方法主要有3种, 分别是: 直方图法(histogram plot)、多度等级分布(rank abundance distribution, RAD)以及累积经验分布函数(empirical cumulative distribution function, ECDF) (McGill, 2010 ).使用直方图法表示物种多度分布时, 需要将物种个体数进行分组, 然而不同的分组方式会影响到图形的表示以及对它的解释(Gray et al, 2006 ).RAD由Whittaker (1965)提出, 作图时x轴表示多度的等级, y轴一般为对数化后的多度.该方法表示的物种多度分布易于解释, 但依然存在两方面的问题, 即进行数学处理时存在困难以及不同的RAD之间不易比较(McGill, 2010 ).由于ECDF能够克服RAD的上述缺点, 尤其是能够很好地体现群落间SAD的差异(Matthews & Whittaker, 2015 ), 因而受到了生态学家的推荐(McGill, 2010 ).本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较. ...
生物群落多样性的测度方法.III. 与物种-多度分布模型有关的统计问题
1
1995
... 图示法可以简单直观地表示物种的多度分布.通常情况下, 表示方法主要有3种, 分别是: 直方图法(histogram plot)、多度等级分布(rank abundance distribution, RAD)以及累积经验分布函数(empirical cumulative distribution function, ECDF) (McGill, 2010 ).使用直方图法表示物种多度分布时, 需要将物种个体数进行分组, 然而不同的分组方式会影响到图形的表示以及对它的解释(Gray et al, 2006 ).RAD由Whittaker (1965)提出, 作图时x轴表示多度的等级, y轴一般为对数化后的多度.该方法表示的物种多度分布易于解释, 但依然存在两方面的问题, 即进行数学处理时存在困难以及不同的RAD之间不易比较(McGill, 2010 ).由于ECDF能够克服RAD的上述缺点, 尤其是能够很好地体现群落间SAD的差异(Matthews & Whittaker, 2015 ), 因而受到了生态学家的推荐(McGill, 2010 ).本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较. ...
物种多度格局研究进展
2
2003
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... (1)复合群落零和多项式模型.该模型假定某一样点的物种多度分布来自于中性复合群落的随机漂变(Alonso & McKane, 2004 ).模型中包括了两个参数: 取样点内的个体数(J )和基本生物多样性指数(fundamental biodiversity number, θ ), 对数级数分布就是本模型的一个特例(Hubbell, 2001 ), 因此两者的拟合效果非常相似.根据该模型, 复合群落内任一取样点内多度为n 的物种数S 可表达为: ...
物种多度格局研究进展
2
2003
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... (1)复合群落零和多项式模型.该模型假定某一样点的物种多度分布来自于中性复合群落的随机漂变(Alonso & McKane, 2004 ).模型中包括了两个参数: 取样点内的个体数(J )和基本生物多样性指数(fundamental biodiversity number, θ ), 对数级数分布就是本模型的一个特例(Hubbell, 2001 ), 因此两者的拟合效果非常相似.根据该模型, 复合群落内任一取样点内多度为n 的物种数S 可表达为: ...
On the relative abundance of bird species. Proceedings of the National Academy of Sciences,
1957
Species abundance distributions: pattern or process?
1
2005
... (2)对数级数模型.对数级数分布是负二项分布在k = 0时的特殊情况, 该模型不考虑没有个体存在的种(Fisher et al, 1943 ; 刘灿然等, 1995 ).根据本模型, 群落内多度为n 的物种数S 可表示为: ...
Explaining the excess of rare species in natural species abundance distributions.
2003
Multimodal species abundance distributions: a deconstruction approach reveals the processes behind the pattern.
2014
Neutral theory and the species abundance distribution: recent developments and prospects for unifying niche and neutral perspectives.
1
2014
... (1)断棍模型.该模型假设某一群落内的总生态位是长度为1的一条短棍, 若将其分割为S 段, 则代表生态位被S 个物种所占有(MacArthur, 1957 ; 程佳佳等, 2011 ).模型假定S 个物种的分类地位和竞争能力均相似, 且在群落中同时出现(程佳佳等, 2011 ; 张姗等, 2015 ).若以J 表示群落内物种的个体总数, 则可将第i 个种的多度A i 表示为: ...
On the species abundance distribution in applied ecology and biodiversity management.
1
2015
... 生态学研究中, 格局和过程之间往往不是一一对应的关系, 因此由格局反推其形成机制的做法存在一定的局限性(Alonso et al, 2008 ; 张姗等, 2015 ).就物种多度格局而言, 对它的分析和理解有助于人们深入认识群落多样性的构建机制, 然而在这过程中它仅是一个必要非充分条件(McGill et al, 2007 ).实践中, 多个机理完全不同的模型在拟合同一组数据时, 其效果可能都较好, 所以单纯基于物种多度格局的模型拟合结果, 并无法充分验证其背后的生态学机制(Volkov et al, 2003 ; Magurran, 2005 ).因而, 基于本文的分析, 我们只能初步认为在天童常绿阔叶林中, 中性过程对常绿和落叶物种多样性格局的形成可能起着更为重要的作用, 而它相对于其他生态学机制(如生态位过程等)的贡献, 则需要结合一系列环境因子、生物因子甚至空间因子进行更为深入的分析(张姗等, 2015 ). ...
Dynamics, diversity, and resource gradient relationships in the herbaceous layer of an old-growth Appalachian forest.
1
2011
... 此外, 生态学家们已经发现, 将具有不同生态特性(如个体大小、扩散能力等)的物种合并考虑时, 可能会造成某些格局(如物种多度分布)潜在的特殊性被掩盖(Matthews et al, 2014 ; Matthews & Whittaker, 2015 ).例如, Magurran和Henderson (2003)发现, 群落整体的物种多度分布格局是其中持久种(persistent species)或核心种(core species)与机会种(occasional species)多度分布的综合体现.所谓持久种(或核心种)是指个体多度较高且在区域内长期存在的物种, 而机会种则不一定在每次调查时都会出现且其多度一般较低(Magurran & Henderson, 2003 ).Magurran和Henderson (2003)将在英国西部一河口地区调查到的鱼类划分为持久种与机会种后, 对它们的物种多度分布进行了分析, 结果显示, 前者表现为对数正态分布, 而后者则呈现出对数级数分布的特点; 但若不进行这类细分, 而是将所有鱼类物种一并考虑的话, 这时的物种多度分布会表现为一种负偏态(negative skew)的形式.虽然本研究中将常绿与落叶物种的物种多度分布进行了独立分析, 但在两种生活型内部, 也必然存在种间的差异, 特别是在物种多度方面的差别.从多度排序上看, 常绿物种中前20位物种的多度之和便已占到其总多度的90.5%; 落叶物种中前26位物种的多度之和也占到落叶物种总多度的近90%, 这说明两者也存在由少数物种在群落中占据较大优势的情况.因而, 根据Magurran和Henderson (2003)的研究结论, 在将生活型内的物种进行混合考虑时, 由于不同的多度分布之间相互重叠, 确实可能造成某些信息的丢失, 从而得出两者物种多度分布格局差异不明显的结论.若要验证并克服这一问题, 则需要在今后的研究中对两种生活型内的物种进行更为细致的划分与分析. ...
Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework.
1
2007
... 此外, 生态学家们已经发现, 将具有不同生态特性(如个体大小、扩散能力等)的物种合并考虑时, 可能会造成某些格局(如物种多度分布)潜在的特殊性被掩盖(Matthews et al, 2014 ; Matthews & Whittaker, 2015 ).例如, Magurran和Henderson (2003)发现, 群落整体的物种多度分布格局是其中持久种(persistent species)或核心种(core species)与机会种(occasional species)多度分布的综合体现.所谓持久种(或核心种)是指个体多度较高且在区域内长期存在的物种, 而机会种则不一定在每次调查时都会出现且其多度一般较低(Magurran & Henderson, 2003 ).Magurran和Henderson (2003)将在英国西部一河口地区调查到的鱼类划分为持久种与机会种后, 对它们的物种多度分布进行了分析, 结果显示, 前者表现为对数正态分布, 而后者则呈现出对数级数分布的特点; 但若不进行这类细分, 而是将所有鱼类物种一并考虑的话, 这时的物种多度分布会表现为一种负偏态(negative skew)的形式.虽然本研究中将常绿与落叶物种的物种多度分布进行了独立分析, 但在两种生活型内部, 也必然存在种间的差异, 特别是在物种多度方面的差别.从多度排序上看, 常绿物种中前20位物种的多度之和便已占到其总多度的90.5%; 落叶物种中前26位物种的多度之和也占到落叶物种总多度的近90%, 这说明两者也存在由少数物种在群落中占据较大优势的情况.因而, 根据Magurran和Henderson (2003)的研究结论, 在将生活型内的物种进行混合考虑时, 由于不同的多度分布之间相互重叠, 确实可能造成某些信息的丢失, 从而得出两者物种多度分布格局差异不明显的结论.若要验证并克服这一问题, 则需要在今后的研究中对两种生活型内的物种进行更为细致的划分与分析. ...
3
2010
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... 生态位模型中的断棍模型无法通过K-S检验, 生态位优先占领模型虽然能够通过K-S检验, 但根据其AIC值可知, 它的拟合效果相比于另外几个模型较为一般.谢玉彬等(2012)使用CCA排序的方法分析了天童常绿阔叶林样地内常绿和落叶物种与3类地形因子(海拔、坡度、地形凸度)之间的关系.他们发现地形因子只能解释两者物种组成变异的19.2% (常绿物种)和7% (落叶物种).这表明至少在地形这一维度上, 生态位理论并不能很好地解释二者各自的多度分布格局, 从而在一定程度上支持了本文的研究结论.此外, 在演替顶极阶段的群落内, 无论是物种组成还是数量比例等都已较为稳定, 种间竞争等生态位过程往往并不明显(闫琰等, 2012 ; 张姗等, 2015 ), 而且同一功能群内部(如常绿或落叶生活型)的各物种之间在生态习性上的差距也相对较小(Siepielski et al, 2010 ; Matthews & Whittaker, 2014 ), 这都有可能会降低生态位过程在常绿与落叶物种多度格局形成过程中的重要性. ...
... 相对地, 两个中性理论模型均能够较好地对天童常绿阔叶林内常绿和落叶木本植物的物种多度分布进行拟合, 这说明相对于生态位过程, 中性过程在两者物种多度分布形成中的作用可能更大.已有研究表明, 生态位格局与中性格局并非是两种相互排斥的群落物种多样性格局, 它们更像是一种连续格局中的两个“端点”, 在两者之间存在着一个逐渐过渡的阶段(Fisher & Mehta, 2014 ).也就是说, 任意群落或许都能够在“纯生态位结构到纯中性结构连续体” (niche-neutrality continuum)上找到自己对应的位置, 例如, 中性群落即可被认为是该连续体上当种间适应性无差异, 且不存在稳定的生态位分化时的特例(Bar-Massada et al, 2014 ; Matthews & Whittaker, 2014 ).因而, 我们推测生态位过程和中性过程在决定群落物种组成中所起的作用可能是此消彼长的, 即当生态位过程的影响下降时, 可能相应地伴随着中性过程作用的增强. ...
On the statistical treatment of communities.
3
1932
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... 图示法可以简单直观地表示物种的多度分布.通常情况下, 表示方法主要有3种, 分别是: 直方图法(histogram plot)、多度等级分布(rank abundance distribution, RAD)以及累积经验分布函数(empirical cumulative distribution function, ECDF) (McGill, 2010 ).使用直方图法表示物种多度分布时, 需要将物种个体数进行分组, 然而不同的分组方式会影响到图形的表示以及对它的解释(Gray et al, 2006 ).RAD由Whittaker (1965)提出, 作图时x轴表示多度的等级, y轴一般为对数化后的多度.该方法表示的物种多度分布易于解释, 但依然存在两方面的问题, 即进行数学处理时存在困难以及不同的RAD之间不易比较(McGill, 2010 ).由于ECDF能够克服RAD的上述缺点, 尤其是能够很好地体现群落间SAD的差异(Matthews & Whittaker, 2015 ), 因而受到了生态学家的推荐(McGill, 2010 ).本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较. ...
... 此外, 生态学家们已经发现, 将具有不同生态特性(如个体大小、扩散能力等)的物种合并考虑时, 可能会造成某些格局(如物种多度分布)潜在的特殊性被掩盖(Matthews et al, 2014 ; Matthews & Whittaker, 2015 ).例如, Magurran和Henderson (2003)发现, 群落整体的物种多度分布格局是其中持久种(persistent species)或核心种(core species)与机会种(occasional species)多度分布的综合体现.所谓持久种(或核心种)是指个体多度较高且在区域内长期存在的物种, 而机会种则不一定在每次调查时都会出现且其多度一般较低(Magurran & Henderson, 2003 ).Magurran和Henderson (2003)将在英国西部一河口地区调查到的鱼类划分为持久种与机会种后, 对它们的物种多度分布进行了分析, 结果显示, 前者表现为对数正态分布, 而后者则呈现出对数级数分布的特点; 但若不进行这类细分, 而是将所有鱼类物种一并考虑的话, 这时的物种多度分布会表现为一种负偏态(negative skew)的形式.虽然本研究中将常绿与落叶物种的物种多度分布进行了独立分析, 但在两种生活型内部, 也必然存在种间的差异, 特别是在物种多度方面的差别.从多度排序上看, 常绿物种中前20位物种的多度之和便已占到其总多度的90.5%; 落叶物种中前26位物种的多度之和也占到落叶物种总多度的近90%, 这说明两者也存在由少数物种在群落中占据较大优势的情况.因而, 根据Magurran和Henderson (2003)的研究结论, 在将生活型内的物种进行混合考虑时, 由于不同的多度分布之间相互重叠, 确实可能造成某些信息的丢失, 从而得出两者物种多度分布格局差异不明显的结论.若要验证并克服这一问题, 则需要在今后的研究中对两种生活型内的物种进行更为细致的划分与分析. ...
The commonness, and rarity, of species.
1
1948
... 天童样地内的79个落叶物种中, 稀有种的比例达46.8%, 而常绿物种中的稀有种只占到其总物种数的24.7%.此外两者在总多度方面也有着十分明显的差异.因此, 为何数量特征差别如此明显的两类物种却有着相近的物种多度分布, 就成了我们所关注的问题.自然界中, 物种组成差异明显但其多度分布却近似相同的情况并不鲜见.例如, 张姗等(2015)在对长白山阔叶红松林25 ha固定监测样地中草本植物多度分布的研究中发现, 虽然随着季节变化, 样地内林下草本层中的植物在组成和数量上有较大差异, 但是不同季节草本层物种多度分布的模型拟合结果却是相似的, 在一定程度上证明不同季节的草本植物群落也可能有着类似的多样性维持机制.McEwan和Muller (2011)在研究美国东北部温带森林林下草本植物多样性的季节变化时亦发现, 同一森林群落内草本植物的多样性格局并未随季节发生明显改变: 在3次调查中(4月、6月和8月), 草本层盖度的最大值均主要出现在海拔较低的阴坡位置; 林下草本植物群落的多样性指标(物种丰富度和均匀度等)在不同季节里也没有显著差异.他们猜测这种情况可能是由于群落发展到顶极阶段后, 草本植物的数量已接近其最大容纳量(maximum species packing), 从而使得草本植物虽然在种类组成上具有季节性, 却有着相近的维持机制(McEwan & Muller, 2011 ).天童样地内的森林为成熟的常绿阔叶林, 因此无论是在当中占据绝对优势的常绿物种, 还是通常以斑块形式存在于其内的落叶物种, 同种生活型内的物种在数量比例等方面可能均已经相对稳定, 所以即使两者在某些多样性指标等方面有所差异, 也并不一定意味着其维持机制必然 不同. ...
R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.
6
2012
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... 生态学研究中, 格局和过程之间往往不是一一对应的关系, 因此由格局反推其形成机制的做法存在一定的局限性(Alonso et al, 2008 ; 张姗等, 2015 ).就物种多度格局而言, 对它的分析和理解有助于人们深入认识群落多样性的构建机制, 然而在这过程中它仅是一个必要非充分条件(McGill et al, 2007 ).实践中, 多个机理完全不同的模型在拟合同一组数据时, 其效果可能都较好, 所以单纯基于物种多度格局的模型拟合结果, 并无法充分验证其背后的生态学机制(Volkov et al, 2003 ; Magurran, 2005 ).因而, 基于本文的分析, 我们只能初步认为在天童常绿阔叶林中, 中性过程对常绿和落叶物种多样性格局的形成可能起着更为重要的作用, 而它相对于其他生态学机制(如生态位过程等)的贡献, 则需要结合一系列环境因子、生物因子甚至空间因子进行更为深入的分析(张姗等, 2015 ). ...
Multivariate and propensity score matching software with automated balance optimization: the matching package for R.
6
2008
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
... 图示法可以简单直观地表示物种的多度分布.通常情况下, 表示方法主要有3种, 分别是: 直方图法(histogram plot)、多度等级分布(rank abundance distribution, RAD)以及累积经验分布函数(empirical cumulative distribution function, ECDF) (McGill, 2010 ).使用直方图法表示物种多度分布时, 需要将物种个体数进行分组, 然而不同的分组方式会影响到图形的表示以及对它的解释(Gray et al, 2006 ).RAD由Whittaker (1965)提出, 作图时x轴表示多度的等级, y轴一般为对数化后的多度.该方法表示的物种多度分布易于解释, 但依然存在两方面的问题, 即进行数学处理时存在困难以及不同的RAD之间不易比较(McGill, 2010 ).由于ECDF能够克服RAD的上述缺点, 尤其是能够很好地体现群落间SAD的差异(Matthews & Whittaker, 2015 ), 因而受到了生态学家的推荐(McGill, 2010 ).本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较. ...
... ).RAD由Whittaker (1965)提出, 作图时x轴表示多度的等级, y轴一般为对数化后的多度.该方法表示的物种多度分布易于解释, 但依然存在两方面的问题, 即进行数学处理时存在困难以及不同的RAD之间不易比较(McGill, 2010 ).由于ECDF能够克服RAD的上述缺点, 尤其是能够很好地体现群落间SAD的差异(Matthews & Whittaker, 2015 ), 因而受到了生态学家的推荐(McGill, 2010 ).本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较. ...
... ), 因而受到了生态学家的推荐(McGill, 2010 ).本文即采用ECDF来表示常绿与落叶物种的多度分布格局, 并利用K-S检验(Kolmogorov-Smirnov test)对两者的差异性进行比较. ...
... 式中, α 代表群落的物种多样性, 类似于物种丰富度的概念(McGill, 2010 ); X 为常数(0 < X ≤ 1), 与群落的大小有关(张姗等, 2015 ). ...
Experimental evidence for neutral community dynamics governing an insect assemblage.
1
2010
... (2)生态位优先占领模型.模型假定种1先占用群落总生态位的k 份, 种2占用剩下的k (1-k )份, 种3再继续占据余下的k (1-k )2 份, 依次类推, 直至剩余资源无法继续维持另一个物种的生存(Motonura, 1932 ; 程佳佳等, 2011 ; 张姗等, 2015 ).本模型中第i 个物种的多度A i 可表示为: ...
The essential characteristics and main types of the broad-leaved evergreen forest in China.
1
1988
... 马克明(2003)和McGill等(2007)均曾对物种多度分布的研究历史作过简要回顾.Raunkiaer是最早对物种多度分布进行定量分析的学者(McGill et al, 2007 ).Motonura (1932)则首次利用几何级数模型(geommetric-series model)拟合了湖泊底栖动物的物种多度分布.自20世纪40年代起, 各类新的模型不断涌现, 对数级数模型(Log-series model) (Fisher et al, 1943 )和对数正态模型(Log-normal model) (Preston, 1948 )正是这期间纯统计模型(purely statistical model)的典型代表.MacArthur (1957)认为在解释实际的物种多度分布时应重视模型的生物学机理, 并提出了著名的断棍模型(broken-stick model).在此之后, 机理模型的研究进入了高速发展的阶段, 它们可大致分为两类, 即生态位模型和中性理论模型.生态位模型, 如断棍模型等, 所关注的是如何将生态位理论与群落物种多度分布相结合; 中性理论模型, 如零和多项式模型(zero-sum multinomial distribution model), 则更强调随机过程对于群落构建的意义(Hubbell, 2001 ).当前, 大多数有关物种多度分布的研究主要集中于利用上述各类模型拟合观测数据, 进而基于拟合效果去推断物种多样性的维持机制(McGill et al, 2007 ; Alonso et al, 2008 ; McGill, 2010 ; White et al, 2012 ). ...
1
1995
... 数据处理过程均基于R-3.2.0 软件(R Core Team, 2012 ).其中, 模型拟合使用sads软件包完成; 基于bootstrap的K-S检验利用Matching软件包完成. ...
1
1995
... 数据处理过程均基于R-3.2.0 软件(R Core Team, 2012 ).其中, 模型拟合使用sads软件包完成; 基于bootstrap的K-S检验利用Matching软件包完成. ...
中国常绿阔叶林8大动态监测样地植被的综合比较
1
2015
... 本研究使用K-S检验对模型的拟合效果进行验证.K-S检验是一种非参数检验的方法, 它通过计算两个样本经验分布函数(empirical distribution function)之间的距离(统计量D )来判断二者是否存在显著差异.为了避免应用该检验方法时出现数据连结的问题, 特别选用了基于bootstrap模拟方法的K-S检验(Sekhon, 2008 ), bootstrap的次数为1,000次.当P < 0.05时, 表明该模型被拒绝. ...
中国常绿阔叶林8大动态监测样地植被的综合比较
1
2015
... 本研究使用K-S检验对模型的拟合效果进行验证.K-S检验是一种非参数检验的方法, 它通过计算两个样本经验分布函数(empirical distribution function)之间的距离(统计量D )来判断二者是否存在显著差异.为了避免应用该检验方法时出现数据连结的问题, 特别选用了基于bootstrap模拟方法的K-S检验(Sekhon, 2008 ), bootstrap的次数为1,000次.当P < 0.05时, 表明该模型被拒绝. ...
A meta-analysis of species-abundance distributions.
1
2010
... 生态位模型中的断棍模型无法通过K-S检验, 生态位优先占领模型虽然能够通过K-S检验, 但根据其AIC值可知, 它的拟合效果相比于另外几个模型较为一般.谢玉彬等(2012)使用CCA排序的方法分析了天童常绿阔叶林样地内常绿和落叶物种与3类地形因子(海拔、坡度、地形凸度)之间的关系.他们发现地形因子只能解释两者物种组成变异的19.2% (常绿物种)和7% (落叶物种).这表明至少在地形这一维度上, 生态位理论并不能很好地解释二者各自的多度分布格局, 从而在一定程度上支持了本文的研究结论.此外, 在演替顶极阶段的群落内, 无论是物种组成还是数量比例等都已较为稳定, 种间竞争等生态位过程往往并不明显(闫琰等, 2012 ; 张姗等, 2015 ), 而且同一功能群内部(如常绿或落叶生活型)的各物种之间在生态习性上的差距也相对较小(Siepielski et al, 2010 ; Matthews & Whittaker, 2014 ), 这都有可能会降低生态位过程在常绿与落叶物种多度格局形成过程中的重要性. ...
Neutral theory and relative species abundance in ecology.
1
2003
... 自然界中, 常绿与落叶物种是较易辨识的两类植物生活型.前者的换叶过程是逐步发生的, 因而从生态外貌上看它们一年四季都是绿色的; 而后者的“新叶”却通常在“老叶”集中掉落后才会生出, 期间有时会相隔数月.常绿和落叶物种作为常绿阔叶林内两种重要的生活型组分(Song, 1988 ; 宋永昌和王祥荣, 1995 ), 对其物种多度分布格局进行分析, 将有助于我们从新的视角理解常绿阔叶林内物种多样性的形成与维持机制.以天童20 ha常绿阔叶林样地内的常绿与落叶物种为例, 前者作为样地中的优势组分, 物种多度最大的细枝柃(Eurya loquaiana )共计20,414株, 常绿稀有种(多度≤ 1株/ha)有18个, 占常绿物种总数的24.66%; 落叶物种中多度最大的南酸枣(Choerospondias axillaris )仅有1,352株, 落叶稀有种则有37个, 占到落叶总物种数的46.84%.基于此, 我们假设: (1)在天童常绿阔叶林中, 常绿与落叶物种的物种多度分布之间应该有着较为明显的差别; (2)主导两者物种多度分布及各自多样性格局形成的生态学过程可能会有所不同. ...
Evergreen broad-leaved forest in Eastern China: its ecology and conservation and the importance of resprouting in forest restoration.
2007
Characterizing species abundance distributions across taxa and ecosystems using a simple maximum entropy model.
3
2012
... 自然界中, 常绿与落叶物种是较易辨识的两类植物生活型.前者的换叶过程是逐步发生的, 因而从生态外貌上看它们一年四季都是绿色的; 而后者的“新叶”却通常在“老叶”集中掉落后才会生出, 期间有时会相隔数月.常绿和落叶物种作为常绿阔叶林内两种重要的生活型组分(Song, 1988 ; 宋永昌和王祥荣, 1995 ), 对其物种多度分布格局进行分析, 将有助于我们从新的视角理解常绿阔叶林内物种多样性的形成与维持机制.以天童20 ha常绿阔叶林样地内的常绿与落叶物种为例, 前者作为样地中的优势组分, 物种多度最大的细枝柃(Eurya loquaiana )共计20,414株, 常绿稀有种(多度≤ 1株/ha)有18个, 占常绿物种总数的24.66%; 落叶物种中多度最大的南酸枣(Choerospondias axillaris )仅有1,352株, 落叶稀有种则有37个, 占到落叶总物种数的46.84%.基于此, 我们假设: (1)在天童常绿阔叶林中, 常绿与落叶物种的物种多度分布之间应该有着较为明显的差别; (2)主导两者物种多度分布及各自多样性格局形成的生态学过程可能会有所不同. ...
... 研究样地位于浙江天童国家森林公园内, 距离宁波市区28 km.区域内气候为典型的亚热带季风性气候, 夏季炎热多雨, 冬季寒冷干燥(宋永昌和王祥荣, 1995 ; Wang et al, 2007 ).根据宁波市鄞州区气象站的记录, 本地年平均温度为16.2°C, 最热月和最冷月分别出现在7月(平均温度28.1°C)和1月(平均温度4.2°C).区域内的年均降水量为1,374.7 mm, 主要集中于每年的5-8月(宋永昌和王祥荣, 1995 ). ...
... ).根据宁波市鄞州区气象站的记录, 本地年平均温度为16.2°C, 最热月和最冷月分别出现在7月(平均温度28.1°C)和1月(平均温度4.2°C).区域内的年均降水量为1,374.7 mm, 主要集中于每年的5-8月(宋永昌和王祥荣, 1995 ). ...
Dominance and diversity in land plant communities: numerical relations of species express the importance of competition in community function and evolution.
1965
基于地形因子的天童地区常绿树种和落叶树种共存机制研究
1
2012
... 天童20 ha常绿阔叶林动态监测样地建成于2010年, 位于森林公园的核心区域(29°48.817ʹ N, 121°47.116ʹ E).样地内的植物群落结构完整, 发育成熟, 为典型的中亚热带常绿阔叶林(杨庆松等, 2011 ; 宋永昌等, 2015 ).整个样地东西长500 m, 南北宽400 m, 地形较为复杂(杨庆松等, 2011 ). ...
基于地形因子的天童地区常绿树种和落叶树种共存机制研究
1
2012
... 天童20 ha常绿阔叶林动态监测样地建成于2010年, 位于森林公园的核心区域(29°48.817ʹ N, 121°47.116ʹ E).样地内的植物群落结构完整, 发育成熟, 为典型的中亚热带常绿阔叶林(杨庆松等, 2011 ; 宋永昌等, 2015 ).整个样地东西长500 m, 南北宽400 m, 地形较为复杂(杨庆松等, 2011 ). ...
长白山不同演替阶段针阔混交林群落物种多度分布格局
1
2012
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
长白山不同演替阶段针阔混交林群落物种多度分布格局
1
2012
... 群落构建, 即群落内物种多样性的形成与维持机制, 一直是生态学研究重点关注的内容(程佳佳等, 2011 ).作为描述群落多样性特征的重要方式之一, 物种多度分布(species abundance distribution, SAD)的形成机制备受瞩目(Borda-de-Água et al, 2012 ).从概念上来说, 物种多度分布是对群落内不同物种多度(个体数量)情况的数量描述(McGill et al, 2007 ).一般地, 局域群落内大多数物种的多度较低, 只有少量物种属于常见种, 这已成为生态学中被广泛接受的法则之一(McGill et al, 2007 ; McGill, 2010 ; Ulrich et al, 2010 ).对于这一生态学中的重要概念, 研究者们一方面对群落物种多度分布本身的特征感兴趣, 另一方面更希望以它为理论基础继而解释其他重要的宏观生态学格局, 如种-面积关系、距离衰减关系甚至群落的构建等(McGill et al, 2007 ; Matthews & Whittaker, 2014 , 2015 ). ...
浙江天童20 ha常绿阔叶林动态监测样地的群落特征
3
2011
... (2) Volkov模型.该模型在拟合群落的物种多度分布时, 相较于复合群落零和多项式模型增加了迁移系数(immigration rate, m ) (Volkov et al, 2003 ), 并假定此迁移系数在物种从复合群落到局域群落的过程中是不变的(张姗等, 2015 ).根据本模型, 局域群落内多度为n 的物种数S 可表示为: ...
... 式中, γ 表示迁移到局域群落内的个体数(Volkov et al, 2003 ; 张姗等, 2015 ). ...
... 生态学研究中, 格局和过程之间往往不是一一对应的关系, 因此由格局反推其形成机制的做法存在一定的局限性(Alonso et al, 2008 ; 张姗等, 2015 ).就物种多度格局而言, 对它的分析和理解有助于人们深入认识群落多样性的构建机制, 然而在这过程中它仅是一个必要非充分条件(McGill et al, 2007 ).实践中, 多个机理完全不同的模型在拟合同一组数据时, 其效果可能都较好, 所以单纯基于物种多度格局的模型拟合结果, 并无法充分验证其背后的生态学机制(Volkov et al, 2003 ; Magurran, 2005 ).因而, 基于本文的分析, 我们只能初步认为在天童常绿阔叶林中, 中性过程对常绿和落叶物种多样性格局的形成可能起着更为重要的作用, 而它相对于其他生态学机制(如生态位过程等)的贡献, 则需要结合一系列环境因子、生物因子甚至空间因子进行更为深入的分析(张姗等, 2015 ). ...
浙江天童20 ha常绿阔叶林动态监测样地的群落特征
3
2011
... (2) Volkov模型.该模型在拟合群落的物种多度分布时, 相较于复合群落零和多项式模型增加了迁移系数(immigration rate, m ) (Volkov et al, 2003 ), 并假定此迁移系数在物种从复合群落到局域群落的过程中是不变的(张姗等, 2015 ).根据本模型, 局域群落内多度为n 的物种数S 可表示为: ...
... 式中, γ 表示迁移到局域群落内的个体数(Volkov et al, 2003 ; 张姗等, 2015 ). ...
... 生态学研究中, 格局和过程之间往往不是一一对应的关系, 因此由格局反推其形成机制的做法存在一定的局限性(Alonso et al, 2008 ; 张姗等, 2015 ).就物种多度格局而言, 对它的分析和理解有助于人们深入认识群落多样性的构建机制, 然而在这过程中它仅是一个必要非充分条件(McGill et al, 2007 ).实践中, 多个机理完全不同的模型在拟合同一组数据时, 其效果可能都较好, 所以单纯基于物种多度格局的模型拟合结果, 并无法充分验证其背后的生态学机制(Volkov et al, 2003 ; Magurran, 2005 ).因而, 基于本文的分析, 我们只能初步认为在天童常绿阔叶林中, 中性过程对常绿和落叶物种多样性格局的形成可能起着更为重要的作用, 而它相对于其他生态学机制(如生态位过程等)的贡献, 则需要结合一系列环境因子、生物因子甚至空间因子进行更为深入的分析(张姗等, 2015 ). ...
长白山阔叶红松林草本层物种多度分布格局及其季节动态
1
2015
... 研究样地位于浙江天童国家森林公园内, 距离宁波市区28 km.区域内气候为典型的亚热带季风性气候, 夏季炎热多雨, 冬季寒冷干燥(宋永昌和王祥荣, 1995 ; Wang et al, 2007 ).根据宁波市鄞州区气象站的记录, 本地年平均温度为16.2°C, 最热月和最冷月分别出现在7月(平均温度28.1°C)和1月(平均温度4.2°C).区域内的年均降水量为1,374.7 mm, 主要集中于每年的5-8月(宋永昌和王祥荣, 1995 ). ...
长白山阔叶红松林草本层物种多度分布格局及其季节动态
1
2015
... 研究样地位于浙江天童国家森林公园内, 距离宁波市区28 km.区域内气候为典型的亚热带季风性气候, 夏季炎热多雨, 冬季寒冷干燥(宋永昌和王祥荣, 1995 ; Wang et al, 2007 ).根据宁波市鄞州区气象站的记录, 本地年平均温度为16.2°C, 最热月和最冷月分别出现在7月(平均温度28.1°C)和1月(平均温度4.2°C).区域内的年均降水量为1,374.7 mm, 主要集中于每年的5-8月(宋永昌和王祥荣, 1995 ). ...